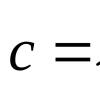Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.

Как обычно, немного самой необходимой теории.

Вектор - это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:

Здесь точка А - начало вектора, а точка В - его конец.

У вектора есть два параметра: его длина и направление.

Длина вектора - это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается

Два вектора называются равными , если они имеют одинаковую длину и сонаправлены.

Два вектора называются сонаправленными , если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:

Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:

Вектора, лежащие на параллельных прямых называются коллинеарными : вектора , и - коллинеарны.

Произведением вектора на число называется вектор, сонаправленный вектору , если title="k>0">, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :

Чтобы сложить два вектора и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :

Это правило сложения векторов называется правилом треугольника .

Чтобы сложить два вектора по правилу параллелограмма , нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:

Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :

Отсюда вытекает правило нахождения разности двух векторов : чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора (то есть конец вычитаемого с концом уменьшаемого):

Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

Предлагаю вам решить задачи из Открытого банка заданий для , а затем сверить све решение с ВИДЕОУРОКАМИ:

1 . Задание 4 (№ 27709)

Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .

2 . Задание 4 (№ 27710)

Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).

3 . Задание 4 (№ 27711)

Две стороны прямоугольника ABCD O . Найдите длину суммы векторов и .

4 . Задание 4 (№ 27712)

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O . Найдите длину разности векторов и . (чертеж из предыдущей задачи).

5 . Задание 4 (№ 27713)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .

6 . Задание 4 (№ 27714)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .

7 .Задание 4 (№ 27715)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора - .(чертеж из предыдущей задачи).

8 .Задание 4 (№ 27716)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора - .

9 . Задание 4 (№ 27717)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .

10 . Задание 4 (№ 27718)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора - .(чертеж из предыдущей задачи).

11 .Задание 4 (№ 27719)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).

12 . Задание 4 (№ 27720)

ABC равны Найдите длину вектора +.

13 . Задание 4 (№ 27721)

Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).

14 . Задание 4 (№ 27722)

Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).

Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр "Час ЕГЭ", попробуйте скачать
Firefox

Еще со школьной скамьи нам известно, что такое вектор – это отрезок, который имеет направление и характеризуется численным значением упорядоченной пары точек. Число, равняющееся длине отрезка, который служит основой, определяется как длина вектора . Для ее определения мы будем использовать систему координат . А также учитываем еще одну характеристику – направление отрезка . Для того, чтобы найти длину вектора, можно воспользоваться двумя способами. Самый простой – берем линейку и измеряем, какова же она будет. А можно воспользоваться формулой. Этот вариант мы сейчас и рассмотрим.

Необходимо:

— система координат (х, у);
— вектор;
— знания по алгебре и геометрии.

Инструкция:

• Формулу определения длины направленного отрезка запишем следующим образом r²= x²+y² . Извлекаем корень квадратный из r² и полученное число будет результатом. Чтобы найти длину вектора, совершаем следующие действия. Обозначаем начальную точку координат (х1;у1) , конечная точка (х2;у2) . Находим x и y путем разности координат конца и начала направленного отрезка. Проще говоря, число (х) определяем по следующей формуле х=х2-х1 , а число (у) соответственно у=у2-у1 .
• Находим квадрат суммы координат по формуле x²+y² . Извлекаем корень квадратный из полученного числа, который и будет длиной вектора (r) . Решение поставленной задачи упростится, если сразу будут известны начальные данные координат направленного отрезка. Все, что потребуется – это подставить данные в формулу.
• Внимание! Вектор может находиться не на плоскости координат, а в пространстве, в таком случае к формуле прибавится еще одно значение, и она будет иметь следующий вид: r²= x²+y²+ z² , где – (z) дополнительная ось, помогающая определить величину направленного отрезка в пространстве.

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу - его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ - единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$=x$, $[ OA_2]=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=^2+^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.

Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:

Понятие вектора

Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!

То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.

Обозначение векторов

Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.

Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Суммой двух векторов АВ и ВС будет являться вектор АС .

Записывается как АВ +ВС =АС .

Это правило называется – правилом треугольника .

То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).

Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b , или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

* * *

Правило параллелограмма

Это правило является следствием изложенного выше.

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a , и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.

Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.

Пусть даны два вектора, найдём их разность:

Мы построили вектор противоположный вектору b, и нашли разность.

Координаты вектора

Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть, координаты вектора представляют собой пару чисел.

Если

И координаты векторов имеют вид:

То c 1 = a 1 + b 1 c 2 = a 2 + b 2

Если

То c 1 = a 1 – b 1 c 2 = a 2 – b 2

Модуль вектора

Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Рассмотрим задачи:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО .

Найдём вектор, который будет являться результатом АО –ВО:

АО –ВО =АО +(–ВО )=АВ

То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ +AD .

Найдём вектор, который будет являться суммой векторов AD и AB BC равен вектору AD . Значит AB +AD =AB +BC =AC

AC это длина диагонали ромба АС , она равна 16.

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО +ВО .

Найдём вектор, который будет являться суммой векторов АО и ВО ВО равен вектору OD, з начит

AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

По теореме Пифагора:

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО –ВО .

Найдём вектор, который будет являться результатом АО –ВО :

АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:

По теореме Пифагора:

Стороны правильного треугольника ABC равны 3.

Найдите длину вектора АВ –АС .

Найдём результат разности векторов:

СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.

27663. Найдите длину вектора а (6;8).

27664. Найдите квадрат длины вектора АВ .

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу - его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ - единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$=x$, $[ OA_2]=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=^2+^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что