Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее - просто прямой ход). Пример такой системы и её решения - на рисунке сверху.

В такой системе последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса , далее - просто обратный ход), из которого находят предыдущую переменную, и так далее.

В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x , а второе уравнение - переменной x .

После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

Преимущества метода:

1. при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера , поскольку при решении методом Гаусса необходимо меньше вычислений;
2. методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
3. можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
4. метод основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.

Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.

Пример 1. Решить систему линейных уравнений, применяя обратный ход:

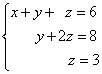
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y :

Теперь нам известны значения уже двух переменных - z и y . Подставляем их в первое уравнение и получаем значение переменной x :

Из предыдущих шагов выписываем решение системы уравнений:

Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.

Элементарные преобразования системы линейных уравнений

Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение - один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.

На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.

При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно :

1. переставлять местами строки (это и было упомянуто в самом начале этой статьи);
2. если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;
3. удалять "нулевые" строки, где все коэффициенты равны нулю;
4. любую строку умножать или делить на некоторое число;
5. к любой строке прибавлять другую строку, умноженное на некоторое число.

В результате преобразований получаем систему линейных уравнений, эквивалентную данной.

Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы

Рассмотрим сначала решение систем линейных уравений, в которых число неизвестных равно числу уравнений. Матрица такой системы - квадратная, то есть в ней число строк равно числу столбцов.

Пример 2. Решить методом Гаусса систему линейных уравнений

Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.

Для упрощения внешнего вида решения составим расширенную матрицу системы :

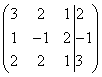
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.

Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы . Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:

С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений . Для этого ко второй строке матрицы прибавим первую строку, умноженную на (в нашем случае на ), к третьей строке – первую строку, умноженную на (в нашем случае на ).

Это возможно, так как

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x :

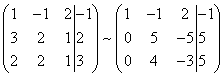
Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:

Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на (в нашем случае на ).

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:

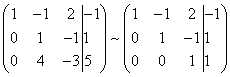
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:

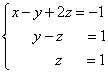
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.

Решение найдём "с конца" - обратный ход . Для этого из последнего уравнения определим z :
.
Подставив это значение в предшествующее уравнение, найдём y :

Из первого уравнения найдём x :

Ответ: решение данной системы уравнений - .

: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.

Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение

Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего демо-примера из алгоритма - здесь уже четыре уравнения и четыре неизвестных.

Пример 4. Решить систему линейных уравнений методом Гаусса:

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу в во втором столбце второй строки. Для этого из второй строки вычтем третью, а полученную в результате вторую строку умножим на -1.

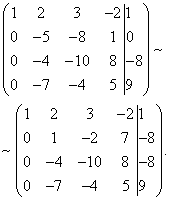
Проведём теперь собственно исключение переменной из третьего и четвёртого уравнений. Для этого к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.

Получили систему уравнений, которой эквивалентна заданная система:

Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной "икс четвёртое":

Это значение подставляем в третье уравнение системы и получаем

,

,

Наконец, подстановка значений

В первое уравнение даёт

,

откуда находим "икс первое":

Ответ: данная система уравнений имеет единственное решение .

Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан тот же ответ, если система имеет однозначное решение.

Решение методом Гаусса прикладных задач на примере задачи на сплавы

Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим одну из таких задач - на сплавы. Аналогичные задачи - задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.

Пример 5. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.

Решение. Составляем систему линейных уравнений:

Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:

Составляем расширенную матрицу системы:

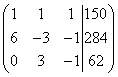
Внимание, прямой ход. Путём сложения (в нашем случае - вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:

Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.

Применяем обратный ход. Находим решение с конца. Видим, что .

Из второго уравнения находим

Из третьего уравнения -

Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан то же ответ, если система имеет однозначное решение.

О простоте метода Гаусса говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение "Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным" - своего рода краткая инструкция по совершению открытий.

Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот - неизвестных меньше, чем уравнений. К решению таких систем уравнений мы сейчас и приступим.

С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.

Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений

Следующий пример - совместная, но неопределённая система линейных уравнений, то есть имеющая бесконечное множество решений.

После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида

Если во всех уравнениях имеющих вид

Свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.

Пример 6.

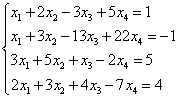
Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную из последующих уравнений. Для этого ко второй, третьей и четвёртой строкам прибавим первую, умноженную соответственно на :

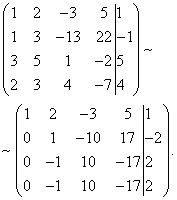
Теперь вторую строку прибавим к третьей и четвёртой.

В результате приходим к системе

Последние два уравнения превратились в уравнения вида . Эти уравнения удовлетворяются при любых значениях неизвестных и их можно отбросить.

Чтобы удовлетворить второму уравнению, мы можем для и выбрать произвольные значения , тогда значение для определится уже однозначно: . Из первого уравнения значение для также находится однозначно: .

Как заданная, так и последняя системы совместны, но неопределённы, и формулы

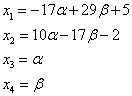
при произвольных и дают нам все решения заданной системы.

Метод Гаусса и системы линейных уравнений, не имеющие решений

Следующий пример - несовместная система линейных уравнений, то есть не имеющая решений. Ответ на такие задачи так и формулируется: система не имеет решений.

Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида

соответствующие уравнению вида

Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. ), то данная система уравнений является несовместной, то есть не имеет решений и на этом её решение закончено.

Пример 7. Решить методом Гаусса систему линейных уравнений:

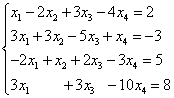
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную . Для этого ко второй строке прибавляем первую, умноженную на , к третьей строке - первую, умноженную на , к четвёртой - первую, умноженную на .

Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Чтобы получить целые отношения коэффициентов, поменяем местами вторую и третью строки расширенной матрицы системы.

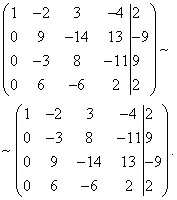
Для исключения из третьего и четвёртого уравнения к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .

Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на .

Заданная система эквивалентна, таким образом, следующей:

Полученная система несовместна, так как её последнее уравнение не может быть удовлетворено никакими значениями неизвестных. Следовательно, данная система не имеет решений.

Рассмотрим точные методы решения системы ; здесь - матрица размерности

Метод решения задачи относят к классу точных, если в предположении отсутствия округлений он дает точное решение задачи после конечного числа арифметических и логических операций. Если число ненулевых элементов матрицы системы имеет порядок , то для большинства используемых в настоящее время точных методов решения таких систем требуемое число операций имеет порядок . Поэтому для применимости точных методов необходимо, чтобы такой порядок числа операций был приемлем для данной ЭВМ; другие ограничения накладываются объемом и структурой памяти ЭВМ.

Оговорка об «используемых в настоящее время методах» имеет следующий смысл. Существуют методы решения таких систем с меньшим порядком числа операций, однако они не используются активно из-за сильной чувствительности результата к вычислительной погрешности.

Наиболее известным из точных методов решения систем линейных уравнений является метод исключения Гаусса. Рассмотрим одну из его возможных реализаций. В предположении, что , первое уравнение системы

делим на коэффициент , в результате получаем уравнение

Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент . В результате эти Уравнения преобразуются к виду

Первое неизвестное оказалось исключенным из всех уравнений, кроме первого. Далее в предположении, что , делим второе уравнение на коэффициент и исключаем неизвестное из всех уравнений, начиная со второго, и т. д. В результате последовательного исключения неизвестных система уравнений преобразуется в систему уравнений с треугольной матрицей

Совокупность проведенных вычислений, в ходе которых исходная задача преобразовалась к виду (2), называется прямым ходом метода Гаусса.

Из уравнения системы (2) определяем , из и т. д. до . Совокупность таких вычислений называют обратным ходом метода Гаусса.

Нетрудно проверить, что реализация прямого хода метода Гаусса требует арифметических операций, а обратного - арифметических операций.

Исключение происходит в результате следующих операций: 1) деления уравнения на , 2) вычитания получающегося после такого деления уравнения, умноженного на , из уравнений с номерами к . Первая операция равносильна умножению системы уравнений слева на диагональную матрицу

вторая операция равносильна умножению слева на матрицу

Таким образом, система (2), получаемая в результате этих преобразований, запишется в виде

Произведение левых (правых) треугольных матриц является левой (правой) треугольной матрицей, поэтому матрица С левая треугольная. Из формулы для элементов обратной матрицы

следует, что матрица, обратная к левой (правой) треугольной, является левой (правой) треугольной. Следовательно, матрица левая треугольная.

Введем обозначение . Согласно построению все и матрица D правая треугольная. Отсюда получаем представление матрицы А в виде произведения левой и правой треугольных матриц:

Равенство вместе с условием , образует систему уравнений относительно элементов треугольных матриц В и : . Поскольку при и при , эта система может быть записана в виде

(3)

или, что то же самое,

Воспользовавшись условием, что все получаем систему рекуррентных соотношений для определения элементов и :

Вычисления проводятся последовательно для совокупностей . Здесь и далее в случае, когда верхний предел суммирования меньше нижнего, считается, что вся сумма равна нулю.

Таким образом, вместо последовательных преобразований системы (1) к виду (2) можно непосредственно произвести вычисление матриц В и с помощью формул (4). Эти вычисления можно осуществить, если только все элементы окажутся отличными от нуля. Пусть - матрицы главных миноров порядка матриц А, В, D. Согласно (3) . Поскольку , то . Следовательно,

Итак, для осуществления вычислений по формулам (4) необходимо и достаточно выполнение условий

В ряде случаев заранее известно, что условие (5) выполнено. Например, многие задачи математической физики сводятся к решению систем с положительно определенной матрицей А. Однако в общем случае этого заранее сказать нельзя. Возможен и такой случай: все , но среди величин есть очень малые и при делении на них будут получаться большие числа с большими абсолютными погрешностями. В результате этого решение сильно исказится.

Обозначим . Поскольку и , то справедливы равенства . Таким образом, после разложения матрицы исходной системы на произведение левой и правой треугольных матриц решение исходной системы сводится к последовательному решению двух систем с треугольными матрицами; это потребует арифметических операций.

Последовательность операций по разложению матрицы А на произведение треугольных матриц и по определению вектора d часто удобно объединить. Уравнения

системы можно записать в виде

Следовательно, значения могут вычисляться одновременно с остальными значениями по формулам (4).

При решении практических задач часто возникает необходимость решения систем уравнений с матрицей, содержащей большое количество нулевых элементов.

Обычно эти матрицы имеют так называемую ленточную структуру. Более точно, матрицу А называют -диагональной или имеющей ленточную структуру, если при . Число называют шириной ленты. Оказывается, что при решении системы уравнений с ленточной матрицей методом Гаусса число арифметических операций и требуемый объем памяти ЭВМ могут быть существенно сокращены.

Задача 1. Исследовать характеристики метода Гаусса и метода решения системы с помощью разложения ленточной матрицы А на произведение левой и правой треугольных матриц. Показать, что для нахождения решения требуется арифметических операций (при ). Найти главный член числа операций при условии .

Задача 2. Оценить объем загружаемой памяти ЭВМ в методе Гаусса для ленточных матриц.

При вычислениях без помощи ЭВМ велика вероятность случайных погрешностей. Для устранения таких погрешностей иногда вводят контрольный системы , состоящий из контрольных элементов уравнений системы

При преобразовании уравнений над контрольными элементами производятся те же операции, что и над свободными членами уравнений. В результате этого контрольный элемент каждого нового уравнения должен равняться сумме коэффициентов этого уравнения. Большое расхождение между ними указывает на погрешности в вычислениях или на неустойчивость алгоритма вычислений по отношению к вычислительной погрешности.

К примеру, в случае приведения системы уравнений к виду с помощью формул (4) контрольный элемент каждого из уравнений системы вычисляется по тем же формулам (4). После вычисления всех элементов при фиксированном контроль осуществляется проверкой равенства

Обратный ход метода Гаусса также сопровождается вычислением контрольных элементов строк системы.

Чтобы избежать катастрофического влияния вычислительной погрешности, применяют метод Гаусса с выбором главного элемента.

Его отличие от описанной выше схемы метода Гаусса состоит в следующем. Пусть по ходу исключения неизвестных получена система уравнений

Найдем такое, что и переобозначим и ; далее произведем исключение неизвестной из всех уравнений, начиная с . Такое переобозначение приводит к изменению порядка исключения неизвестных и во многих случаях существенно уменьшает чувствительность решения к погрешностям округления при вычислениях.

Часто требуется решить несколько систем уравнений , с одной и той же матрицей А. Удобно поступить следующим образом: введя обозначения

произведем вычисления по формулам (4), причем элементы вычислим при . В результате будут получены р систем уравнений с треугольной матрицей, соответствующих исходной задаче

Решаем эти системы каждую в отдельности. Оказывается, что общее число арифметических действий при решении р систем уравнений таким способом .

Описанный выше прием иногда используется для того, чтобы без существенных дополнительных затрат получить суждение о погрешности решения, являющейся следствием погрешностей округления при вычислениях. Задаются вектором z с компонентами, имеющими по возможности тот же порядок и знак, что и компоненты искомого решения; часто из-за отсутствия достаточной информации берут . Вычисляется вектор , и наряду с исходной системой уравнений решается система .

Пусть и z - реально получаемые решения этих систем. Суждение о погрешности искомого решения можно получить, основываясь на гипотезе: относительные погрешности при решении методом исключения систем с одной и той же матрицей и различными правыми частями, которыми являются соответственно величины и , отличаются не в очень большое число раз.

Другой прием для получения суждения о реальной величине погрешности, возникающей за счет округлений при вычислениях, состоит в изменении масштабов, меняющем картину накопления вычислительной погрешности.

Наряду с исходной системой тем же методом решается система

При и , не являющихся целыми степенями двойки, сравнение векторов и дает представление о величине вычислительной погрешности. Например, можно взять .

Изучение многих задач приводит к необходимости решения систем линейных уравнений с симметричной положительно определенной матрицей. Такие системы возникают, например, при решении дифференциальных уравнений методом конечных элементов или же конечно-разностными методами. В этих случаях матрица системы имеет также и ленточную структуру.

Для решения таких систем, а также систем уравнений более общего вида с эрмитовой не обязательно положительно определенной матрицей применяется метод квадратного корня (метод Холецкого). Матрица А представляется в виде

где S - правая треугольная матрица, - сопряженная с ней, т. е.

причем все - диагональная матрица с элементами , равными или -1. Матричное равенство (6) образует систему уравнений

Аналогичные уравнения при отброшены, так как уравнения, соответствующие парам и , эквивалентны. Отсюда получаем рекуррентные формулы для определения элементов и :

Матрица S является правой треугольной, и, таким образом, после получения представления (6) решение исходной системы также сводится к Последовательному решению двух систем с треугольными матрицами. Заметим, что в случае все и .

Задача 3. Оценить число арифметических операций и загрузку памяти ЭВМ (при условии объем памяти, требуемый для запоминания матрицы А, уменьшается) при решении системы с вещественной положительно определеннной матрицей А методом квадратного корня.

Многие пакеты прикладных программ для решения краевых задач математической физики методом конечных элементов организованы по следующей схеме. После формирования матрицы системы А путем перестановки строк и столбцов (одновременно переставляются и строки и и столбцы) система преобразуется к виду с наименьшей шириной ленты. Далее применяется метод квадратного корня. При этом с целью уменьшения объема вычислений при решении системы с другими правыми частями матрица S запоминается.

Раздел 3. Численные методы решения уравнений

Виды математических моделей (уравнений) в теории электрических цепей

1. - системы линейных алгебраических уравнений –

линейные цепи постоянного и синусоидального переменного (комплексный метод) тока.

2 . - системы нелинейных алгебраических или

трансцендентных уравнений – нелинейные цепи постоянного или синусоидального тока.

3. . – системы нелинейных дифференциальных

уравнений первого порядка в обыкновенных производных – переходные процессы в нелинейных цепях.

Здесь F и ψ – вектор-функции, т.е. эквивалентно записи:

f 1 (X,b 1) = 0

f 2 (X,b 2) = 0

…………

f n (X,b n) = 0

а - записи:

ψ 1 (dX/dt,X,b 1 ,t) = 0

ψ 2 (dX/dt,X,b 2 ,t) = 0

…………………..

ψ n (dX/dt,X,b n ,t) = 0

Рассмотрим наиболее эффективные методы решения этих уравнений.

Численные методы решения систем линейных алгебраических уравнений (ЛАУ)

Метод Гаусса (исключения неизвестных)

Методы решения ЛАУ имеют важное значение, так как они применяются (итерационно) для решения более сложных уравнений.

Пусть система ЛАУ задана в виде:

,

где - квадратная матрица n – го порядка с ненулевыми диагональными элементами ; - вектор неизвестных; - вектор правых частей.

Алгоритм метода Гаусса состоит из прямого и обратного хода. Во время прямого хода осуществляется последовательное исключение неизвестных. Система приобретает вид:

Пересчет коэффициентов производится по формуле:

, где i, j = k+1, …n при исключение k -го неизвестного.

При этом столбец правых частей удобно рассматривать как n + 1 столбец матрицы коэффициентов , т.е. j = k+1, …n+1.

Обратный ход заключается в определении неизвестных, начиная с последнего уравнения где осталась одна неизвестная x n . Полученное значение x n подставляется в предыдущее уравнение и определяется x n -1 и т.д.

Для произвольного x k получается следующая формула:

где k = n, n -1,…1.

Трудоемкость метода Гаусса оценивается количеством выполняемых арифметических операций:

.

Кубическая зависимость от размерности задачи существенно ограничивает сложность анализируемых цепей. Однако если часть коэффициентов a ik в матрице равна нулю, т.е. она является разреженной , то появляется возможность сокращения трудоемкости.

Основная идея метода разреженных матриц состоит в учете при вычислениях и хранении только ненулевых элементов матрицы . Степень разреженности матрицы характеризуется коэффициентом заполнения:

где n ннэ –число ненулевых элементов.

Существуют матрицы коэффициентов специального вида: ленточные, когда ненулевые элементы располагаются вдоль главной диагонали; и блочно-диагональные, когда вдоль главной диагонали располагаются ненулевые блоки. Еще встречаются блочно-диагональные с окаймлением.

Пример ленточной матрицы Пример блочно-диагональной матрицы

Пример блочно-диагональной матрицы с окаймлением

Для них разработаны специальные эффективные методы решения. Для диагональной – метод прогонки . Блочная распадается на отдельные группы уравнений по блокам, которые решаются методом Гаусса. Для блочно-диагональных с окаймлением существуют диакоптические методы решения.

Диакоптика – подход к исследованию сложных систем, заключающейся в расчленение системы на части и её анализе по частям при учете всех связей между выделенными частями.

Две системы линейных уравнений называются равносильными, если множество всех их решений совпадает.

Элементарные преобразования системы уравнений - это:

1. Вычеркивание из системы тривиальных уравнений, т.е. таких, у которых все коэффициенты равны нулю;
2. Умножение любого уравнения на число, отличное от нуля;
3. Прибавление к любому i -му уравнению любого j -то уравнения, умноженного на любое число.

Переменная x i называется свободной, если эта переменная не является разрешенной, а вся система уравнений - является разрешенной.

Теорема. Элементарные преобразования переводят систему уравнений в равносильную.

Смысл метода Гаусса заключается в том, чтобы преобразовать исходную систему уравнений и получить равносильную разрешенную или равносильную несовместную систему.

Итак, метод Гаусса состоит из следующих шагов:

1. Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная x i входит с коэффициентом 1;
2. Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной x i в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной x i , и равносильную исходной;
3. Если возникают тривиальные уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы. В результате уравнений становится на одно меньше;
4. Повторяем предыдущие шаги не более n раз, где n - число уравнений в системе. Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.

В результате через несколько шагов получим либо разрешенную систему (возможно, со свободными переменными), либо несовместную. Разрешенные системы распадаются на два случая:

1. Число переменных равно числу уравнений. Значит, система определена;
2. Число переменных больше числа уравнений. Собираем все свободные переменные справа - получаем формулы для разрешенных переменных. Эти формулы так и записываются в ответ.

Вот и все! Система линейных уравнений решена! Это довольно простой алгоритм, и для его освоения вам не обязательно обращаться к репетитору высшей по математике. Рассмотрим пример:

Задача. Решить систему уравнений:

Описание шагов:

1. Вычитаем первое уравнение из второго и третьего - получим разрешенную переменную x 1 ;
2. Умножаем второе уравнение на (−1), а третье уравнение делим на (−3) - получим два уравнения, в которых переменная x 2 входит с коэффициентом 1;
3. Прибавляем второе уравнение к первому, а из третьего - вычитаем. Получим разрешенную переменную x 2 ;
4. Наконец, вычитаем третье уравнение из первого - получаем разрешенную переменную x 3 ;
5. Получили разрешенную систему, записываем ответ.

Общее решение совместной системы линейных уравнений - это новая система, равносильная исходной, в которой все разрешенные переменные выражены через свободные.

Когда может понадобиться общее решение? Если приходится делать меньше шагов, чем k (k - это сколько всего уравнений). Однако причин, по которым процесс заканчивается на некотором шаге l < k , может быть две:

1. После l -го шага получилась система, которая не содержит уравнения с номером (l + 1). На самом деле это хорошо, т.к. разрешенная система все равно получена - даже на несколько шагов раньше.
2. После l -го шага получили уравнение, в котором все коэффициенты при переменных равны нулю, а свободный коэффициент отличен от нуля. Это противоречивое уравнение, а, следовательно, система несовместна.

Важно понимать, что возникновение противоречивого уравнения по методу Гаусса - это достаточное основание несовместности. При этом заметим, что в результате l -го шага не может остаться тривиальных уравнений - все они вычеркиваются прямо в процессе.

Описание шагов:

1. Вычитаем первое уравнение, умноженное на 4, из второго. А также прибавляем первое уравнение к третьему - получим разрешенную переменную x 1 ;
2. Вычитаем третье уравнение, умноженное на 2, из второго - получим противоречивое уравнение 0 = −5.

Итак, система несовместна, поскольку обнаружено противоречивое уравнение.

Задача. Исследовать совместность и найти общее решение системы:

Описание шагов:

1. Вычитаем первое уравнение из второго (предварительно умножив на два) и третьего - получим разрешенную переменную x 1 ;
2. Вычитаем второе уравнение из третьего. Поскольку все коэффициенты в этих уравнениях совпадают, третье уравнение превратится в тривиальное. Заодно умножим второе уравнение на (−1);
3. Вычитаем из первого уравнения второе - получим разрешенную переменную x 2 . Вся система уравнений теперь тоже разрешенная;
4. Поскольку переменные x 3 и x 4 - свободные, переносим их вправо, чтобы выразить разрешенные переменные. Это и есть ответ.

Итак, система совместная и неопределенная, поскольку есть две разрешенных переменных (x 1 и x 2) и две свободных (x 3 и x 4).

Рассмотрим систему m линейных уравнений с n неизвестными

Элементарными преобразованиями системы (4.12) называют:

1. перестановку любых двух уравнений;
2. умножение обеих частей любого уравнения на любое число, отличное от нуля;
3. прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.

Очевидно, что элементарные преобразования переводят линейную систему в эквивалентную.

Ступенчатой системой называется система линейных уравнений вида

(4.13)

где . Коэффициенты a ii называются главными , или ведущими , элементами системы. Например, система

Имеет ступенчатый вид.

Если в системе (4.13) k = n , то ее называют треугольной . Очевидно, что в этом случае она является определенной.

Если k < n , то k неизвестных х 1 , х 2 , ..., х к , называют главными элементами . Они могут быть выражены через остальные n – k неизвестные, называемые свободными . В этом случае система (4.13) будет называться неопределенной .

Вернемся к произвольной системе (4.12) и для определенности будем считать, что . Если это не так, то тождественными линейными преобразованиями системы (4.12) можно всегда добиться выполнения данного условия. Исключим х 1 из всех уравнений, кроме первого. Для этого обе части первого уравнения умножим на a 21 /a 11 и вычтем из соответствующих частей второго уравнения. Затем обе части первого уравнения умножим на a 31 /a 11 и вычтем из соответствующих частей третьего. И так поступим с каждым следующим уравнением. Далее таким же образом исключаем х 2 из третьего, четвертого и так далее уравнений. В результате таких преобразований мы получим совместную ступенчатую систему или придем к несовместимой системе, в которой одно из уравнений имеет отличный от нуля свободный член, а все остальные коэффициенты левой части равны нулю. В последнем случае система (4.12) также будет несовместимой.

Пример 6 . Решить систему

Решение . Вычисления удобно записывать по так называемой схеме единственного деления, в которой оперируют с коэффициентами системы .

X 1	X 2	X 3	B
1	2	1	9	13
1	1	2	8	12
2	1	1	7	11
1	2	1	9	13
0	-1	1	-1	-1
0	-3	-1	11	15
1	2	1	9	13
0	-1	1	-1	-1
0	0	-4	-8	-12

В результате получаем треугольную систему.