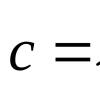Кривые Римана Затем Эйнштейн узнал о немецком математике Георге Фридрихе Бернхарде Римане, который пошел в создании криволинейной геометрии дальше Лобачевского. В 1854 г. он вообразил, что пространство может быть искривленным. По сути дела, он разработал именно ту

Наследие Римана

Наследие Римана Риман упорно продолжал исследования в области физики. В 1858 г. он даже объявил, что наконец сформулировал единое описание для света и электричества. Он писал: «Я полностью убежден, что моя теория верна и что через несколько лет ее признают таковой».

Коши

Условия Коши - Римана , называемые также условиями Даламбера - Эйлера - соотношения, связывающие вещественную $u=u(x,y)$ и мнимую $v=v(x,y)$ части всякой дифференцируемой функции комплексного переменного $w=f(z)=u+iv,\backslash \; z=x+iy$.

Формулировка

В декартовых координатах

Для того чтобы функция $w=f(z)$, определённая в некоторой области $D$ комплексной плоскости , была дифференцируема в точке $z\_0=x\_0+iy\_0$ как функция комплексного переменного $z$, необходимо и достаточно, чтобы её вещественная и мнимая части $u$ и $v$ были дифференцируемы в точке $(x\_0,y\_0)$ как функции вещественных переменных $x$ и $y$ и чтобы, кроме того, в этой точке выполнялись условия Коши - Римана:

$\backslash frac\{\backslash partial\; u\}\{\backslash partial\; x\}=\backslash frac\{\backslash partial\; v\}\{\backslash partial\; y\}\; ;$ $\backslash frac\{\backslash partial\; u\}\{\backslash partial\; y\}=\; -\backslash frac\{\backslash partial\; v\}\{\backslash partial\; x\}\; .$

Компактная запись:

$\backslash frac\{\backslash partial\; f\}\{\backslash partial\; x\}\; +\; i\; \backslash frac\{\backslash partial\; f\}\{\backslash partial\; y\}\; =\; 0\; .$

Если условия Коши - Римана выполнены, то производная $f"(z)$ представима в любой из следующих форм:

$f"(z)\; =\; \backslash frac\{\backslash partial\; u\}\{\backslash partial\; x\}\; +\; i\; \backslash frac\{\backslash partial\; v\}\{\backslash partial\; x\}\; =\; \backslash frac\{\backslash partial\; v\}\{\backslash partial\; y\}\; -\; i\; \backslash frac\{\backslash partial\; u\}\{\backslash partial\; y\}=\backslash frac\{\backslash partial\; u\}\{\backslash partial\; x\}\; -\; i\; \backslash frac\{\backslash partial\; u\}\{\backslash partial\; y\}=\backslash frac\{\backslash partial\; v\}\{\backslash partial\; y\}+i\; \backslash frac\{\backslash partial\; v\}\{\backslash partial\; x\}.$

Доказательство

1. Необходимость

По условию теоремы существует предел

$f"(z\_0)\; =\; \backslash lim\backslash limits\_\{\backslash Delta\; z\; \backslash to\; 0\}\; \backslash frac\{f(z\_0+\backslash Delta\; z)-f(z\_0)\}\{\backslash Delta\; z\}$,

не зависящий от способа стремления $\backslash Delta\; z$ к нулю. Положим $\backslash Delta\; z\; =\; \backslash Delta\; x$ и рассмотрим выражение

$f"(z\_0)\; =\; \backslash lim\backslash limits\_\{\backslash Delta\; x\; \backslash to\; 0\}\; \backslash frac\{u(x\_0+\backslash Delta\; x,\; y\_0)-u(x\_0,\; y\_0)\}\{\backslash Delta\; x\}\; +\; i\; \backslash lim\backslash limits\_\{\backslash Delta\; x\; \backslash to\; 0\}\; \backslash frac\{v(x\_0+\backslash Delta\; x,\; y\_0)-v(x\_0,\; y\_0)\}\{\backslash Delta\; x\}$.

Из существования предела комплексного выражения следует существование действительной и мнимой его частей. Поэтому в точке $x\_0,\; y\_0$ существуют частные производные по x функций u(x,y) и v(x,y) и имеет место формула

$f"(z\_0)\; =\; u\_x(x\_0,\; y\_0)+iv\_x(x\_0,\; y\_0)$

Полагая $\backslash Delta\; z\; =\; i\; \backslash Delta\; y$, находим

$f"(z\_0)\; =\; \backslash lim\backslash limits\_\{\backslash Delta\; y\; \backslash to\; 0\}\; \backslash frac\{u(x\_0,\; y\_0+\backslash Delta\; y)-u(x\_0,\; y\_0)\}\{i\; \backslash Delta\; y\}\; +\; i\; \backslash lim\backslash limits\_\{\backslash Delta\; y\; \backslash to\; 0\}\; \backslash frac\{v(x\_0,\; y\_0+\backslash Delta\; y)-v(x\_0,\; y\_0)\}\{i\; \backslash Delta\; y\}\; =\; -iu\_y(x\_0,\; y\_0)+v\_y(x\_0,\; y\_0)$.

Сравнивая две последние формулы, убеждаемся в справедливости условий Коши-Римана.

2. Достаточность

По определению дифференцируемости, приращения функций $u(x,y)$ и $v(x,y)$ в окрестности точки $(x\_0,\; y\_0)$ могут быть записаны в виде

$u(x\_0+\backslash Delta\; x,\; y\_0\; +\; \backslash Delta\; y)-u(x\_0,\; y\_0)=\; u\_x(x\_0,y\_0)\backslash Delta\; x\; +\; u\_y(x\_0,y\_0)\backslash Delta\; y\; +\backslash xi(x,y)$, $v(x\_0+\backslash Delta\; x,\; y\_0\; +\; \backslash Delta\; y)-v(x\_0,\; y\_0)=\; v\_x(x\_0,y\_0)\backslash Delta\; x\; +\; v\_y(x\_0,y\_0)\backslash Delta\; y\; +\backslash eta(x,y)$,

где функции $\backslash xi(x,y)$ и $\backslash eta(x,y)$ стремятся к нулю при $x\; \backslash rightarrow\; x\_0$, $y\; \backslash rightarrow\; y\_0$ быстрее, чем $\backslash Delta\; x$ и $\backslash Delta\; y\backslash qquad$ $\backslash left(\backslash lim\backslash limits\_\{|\backslash Delta\; z|\; \backslash to\; 0\}\; \backslash frac\{\backslash xi(x,y)\}\{|\backslash Delta\; z|\}=0\backslash right.$, $\backslash lim\backslash limits\_\{|\backslash Delta\; z|\; \backslash to\; 0\}\; \backslash frac\{\backslash eta(x,y)\}\{|\backslash Delta\; z|\}=0$, $\backslash left.|\backslash Delta\; z|=\backslash sqrt\{(\backslash Delta\; x)^2+(\backslash Delta\; y)^2\}\backslash right)$. Составим теперь разностное соотношение $\backslash frac\{f(z\_0+\backslash Delta\; z)-f(z\_0)\}\{\backslash Delta\; z\}$, где $\backslash Delta\; z\; =\; \backslash Delta\; x\; +\; i\; \backslash Delta\; y$ и преобразуем его к виду

$\backslash frac\{f(z\_0+\backslash Delta\; z)-f(z\_0)\}\{\backslash Delta\; z\}\; =\; u\_x(x\_0,\; y\_0)\backslash frac\{\backslash Delta\; x\; +\; i\; \backslash Delta\; y\}\{\backslash Delta\; x\; +\; i\; \backslash Delta\; y\}\; +\; v\_x(x\_0,\; y\_0)\backslash frac\{i\; \backslash Delta\; x\; -\; \backslash Delta\; y\}\{\backslash Delta\; x\; +\; i\; \backslash Delta\; y\}\; +\; \backslash frac\{\backslash xi(x,y)+i\backslash eta(x,y)\}\{\backslash Delta\; x\; +\; i\; \backslash Delta\; y\}\; =\; u\_x(x\_0,\; y\_0)\; +\; iv\_x(x\_0,\; y\_0)+\backslash frac\{\backslash zeta(z)\}\{\backslash Delta\; z\}$ $(\backslash zeta(z)\; =\; \backslash xi(x,y)+i\backslash eta(x,y))$.

Заметим, что при стремлении $\backslash Delta\; z$ к нулю последнее слагаемое этой формулы стремится к нулю, а первые остаются неизменными. Поэтому существует предел $\backslash lim\backslash limits\_\{\backslash Delta\; z\; \backslash to\; 0\}\; \backslash frac\{f(z\_0+\backslash Delta\; z)-f(z\_0)\}\{\backslash Delta\; z\}\; =\; f"(z\_0)$, что и доказывает дифференцируемость функции $f(z)$ в точке $z\_0$.

В полярных координатах

См. также

Напишите отзыв о статье "Условия Коши - Римана"

Литература

• Евграфов М. А. Аналитические функции. - 2-е изд., перераб. и дополн. - М .: Наука , . - 472 с.
• Привалов И. И. Введение в теорию функций комплексного переменного: Пособие для высшей школы. - М.-Л.: Государственное издательство, . - 316 с.
• Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. - М .: Наука, 1974. - 320 с.
• Титчмарш Е. Теория функций: Пер. с англ. - 2-е изд., перераб. - М .: Наука , . - 464 с.
• Шабат Б. В. Введение в комплексный анализ. - М .: Наука , . - 577 с.
• Картан А. Дифференциальное исчисление. Дифференциальные формы. - М .: Мир , . - 392 с.

Отрывок, характеризующий Условия Коши - Римана

Библейское предание говорит, что отсутствие труда – праздность была условием блаженства первого человека до его падения. Любовь к праздности осталась та же и в падшем человеке, но проклятие всё тяготеет над человеком, и не только потому, что мы в поте лица должны снискивать хлеб свой, но потому, что по нравственным свойствам своим мы не можем быть праздны и спокойны. Тайный голос говорит, что мы должны быть виновны за то, что праздны. Ежели бы мог человек найти состояние, в котором он, будучи праздным, чувствовал бы себя полезным и исполняющим свой долг, он бы нашел одну сторону первобытного блаженства. И таким состоянием обязательной и безупречной праздности пользуется целое сословие – сословие военное. В этой то обязательной и безупречной праздности состояла и будет состоять главная привлекательность военной службы.
Николай Ростов испытывал вполне это блаженство, после 1807 года продолжая служить в Павлоградском полку, в котором он уже командовал эскадроном, принятым от Денисова.
Ростов сделался загрубелым, добрым малым, которого московские знакомые нашли бы несколько mauvais genre [дурного тона], но который был любим и уважаем товарищами, подчиненными и начальством и который был доволен своей жизнью. В последнее время, в 1809 году, он чаще в письмах из дому находил сетования матери на то, что дела расстраиваются хуже и хуже, и что пора бы ему приехать домой, обрадовать и успокоить стариков родителей.
Читая эти письма, Николай испытывал страх, что хотят вывести его из той среды, в которой он, оградив себя от всей житейской путаницы, жил так тихо и спокойно. Он чувствовал, что рано или поздно придется опять вступить в тот омут жизни с расстройствами и поправлениями дел, с учетами управляющих, ссорами, интригами, с связями, с обществом, с любовью Сони и обещанием ей. Всё это было страшно трудно, запутано, и он отвечал на письма матери, холодными классическими письмами, начинавшимися: Ma chere maman [Моя милая матушка] и кончавшимися: votre obeissant fils, [Ваш послушный сын,] умалчивая о том, когда он намерен приехать. В 1810 году он получил письма родных, в которых извещали его о помолвке Наташи с Болконским и о том, что свадьба будет через год, потому что старый князь не согласен. Это письмо огорчило, оскорбило Николая. Во первых, ему жалко было потерять из дома Наташу, которую он любил больше всех из семьи; во вторых, он с своей гусарской точки зрения жалел о том, что его не было при этом, потому что он бы показал этому Болконскому, что совсем не такая большая честь родство с ним и что, ежели он любит Наташу, то может обойтись и без разрешения сумасбродного отца. Минуту он колебался не попроситься ли в отпуск, чтоб увидать Наташу невестой, но тут подошли маневры, пришли соображения о Соне, о путанице, и Николай опять отложил. Но весной того же года он получил письмо матери, писавшей тайно от графа, и письмо это убедило его ехать. Она писала, что ежели Николай не приедет и не возьмется за дела, то всё именье пойдет с молотка и все пойдут по миру. Граф так слаб, так вверился Митеньке, и так добр, и так все его обманывают, что всё идет хуже и хуже. «Ради Бога, умоляю тебя, приезжай сейчас же, ежели ты не хочешь сделать меня и всё твое семейство несчастными», писала графиня.
Письмо это подействовало на Николая. У него был тот здравый смысл посредственности, который показывал ему, что было должно.
Теперь должно было ехать, если не в отставку, то в отпуск. Почему надо было ехать, он не знал; но выспавшись после обеда, он велел оседлать серого Марса, давно не езженного и страшно злого жеребца, и вернувшись на взмыленном жеребце домой, объявил Лаврушке (лакей Денисова остался у Ростова) и пришедшим вечером товарищам, что подает в отпуск и едет домой. Как ни трудно и странно было ему думать, что он уедет и не узнает из штаба (что ему особенно интересно было), произведен ли он будет в ротмистры, или получит Анну за последние маневры; как ни странно было думать, что он так и уедет, не продав графу Голуховскому тройку саврасых, которых польский граф торговал у него, и которых Ростов на пари бил, что продаст за 2 тысячи, как ни непонятно казалось, что без него будет тот бал, который гусары должны были дать панне Пшаздецкой в пику уланам, дававшим бал своей панне Боржозовской, – он знал, что надо ехать из этого ясного, хорошего мира куда то туда, где всё было вздор и путаница.
Через неделю вышел отпуск. Гусары товарищи не только по полку, но и по бригаде, дали обед Ростову, стоивший с головы по 15 руб. подписки, – играли две музыки, пели два хора песенников; Ростов плясал трепака с майором Басовым; пьяные офицеры качали, обнимали и уронили Ростова; солдаты третьего эскадрона еще раз качали его, и кричали ура! Потом Ростова положили в сани и проводили до первой станции.
До половины дороги, как это всегда бывает, от Кременчуга до Киева, все мысли Ростова были еще назади – в эскадроне; но перевалившись за половину, он уже начал забывать тройку саврасых, своего вахмистра Дожойвейку, и беспокойно начал спрашивать себя о том, что и как он найдет в Отрадном. Чем ближе он подъезжал, тем сильнее, гораздо сильнее (как будто нравственное чувство было подчинено тому же закону скорости падения тел в квадратах расстояний), он думал о своем доме; на последней перед Отрадным станции, дал ямщику три рубля на водку, и как мальчик задыхаясь вбежал на крыльцо дома.
После восторгов встречи, и после того странного чувства неудовлетворения в сравнении с тем, чего ожидаешь – всё то же, к чему же я так торопился! – Николай стал вживаться в свой старый мир дома. Отец и мать были те же, они только немного постарели. Новое в них било какое то беспокойство и иногда несогласие, которого не бывало прежде и которое, как скоро узнал Николай, происходило от дурного положения дел. Соне был уже двадцатый год. Она уже остановилась хорошеть, ничего не обещала больше того, что в ней было; но и этого было достаточно. Она вся дышала счастьем и любовью с тех пор как приехал Николай, и верная, непоколебимая любовь этой девушки радостно действовала на него. Петя и Наташа больше всех удивили Николая. Петя был уже большой, тринадцатилетний, красивый, весело и умно шаловливый мальчик, у которого уже ломался голос. На Наташу Николай долго удивлялся, и смеялся, глядя на нее.
– Совсем не та, – говорил он.
– Что ж, подурнела?
– Напротив, но важность какая то. Княгиня! – сказал он ей шопотом.
– Да, да, да, – радостно говорила Наташа.
Наташа рассказала ему свой роман с князем Андреем, его приезд в Отрадное и показала его последнее письмо.
– Что ж ты рад? – спрашивала Наташа. – Я так теперь спокойна, счастлива.
– Очень рад, – отвечал Николай. – Он отличный человек. Что ж ты очень влюблена?
– Как тебе сказать, – отвечала Наташа, – я была влюблена в Бориса, в учителя, в Денисова, но это совсем не то. Мне покойно, твердо. Я знаю, что лучше его не бывает людей, и мне так спокойно, хорошо теперь. Совсем не так, как прежде…
Николай выразил Наташе свое неудовольствие о том, что свадьба была отложена на год; но Наташа с ожесточением напустилась на брата, доказывая ему, что это не могло быть иначе, что дурно бы было вступить в семью против воли отца, что она сама этого хотела.
– Ты совсем, совсем не понимаешь, – говорила она. Николай замолчал и согласился с нею.
Брат часто удивлялся глядя на нее. Совсем не было похоже, чтобы она была влюбленная невеста в разлуке с своим женихом. Она была ровна, спокойна, весела совершенно по прежнему. Николая это удивляло и даже заставляло недоверчиво смотреть на сватовство Болконского. Он не верил в то, что ее судьба уже решена, тем более, что он не видал с нею князя Андрея. Ему всё казалось, что что нибудь не то, в этом предполагаемом браке.
«Зачем отсрочка? Зачем не обручились?» думал он. Разговорившись раз с матерью о сестре, он, к удивлению своему и отчасти к удовольствию, нашел, что мать точно так же в глубине души иногда недоверчиво смотрела на этот брак.
– Вот пишет, – говорила она, показывая сыну письмо князя Андрея с тем затаенным чувством недоброжелательства, которое всегда есть у матери против будущего супружеского счастия дочери, – пишет, что не приедет раньше декабря. Какое же это дело может задержать его? Верно болезнь! Здоровье слабое очень. Ты не говори Наташе. Ты не смотри, что она весела: это уж последнее девичье время доживает, а я знаю, что с ней делается всякий раз, как письма его получаем. А впрочем Бог даст, всё и хорошо будет, – заключала она всякий раз: – он отличный человек.

Пусть функция =u (x,y )+iv (x,y ) определена в окрестности точки z = x +iy . Если переменной z придать приращение  z = x +i  y , то функция
получит приращение


= (z + z )–
=u (x + x , y + y )+

+ iv (x + x , y + y ) - u (x,y ) - iv (x,y ) = [u (x + x , y + y ) –

– u (x,y )] + i [v (x + x , y + y ) - v (x,y )] =

= u (x,y ) + i  v (x,y ).

Определение. Если существует предел

=

,

то этот предел называется производной от функции
в точкеz и обозначается через f (z ) или
. Таким образом, по определению,

=

=

. (1.37)

Если функция
имеет производную в точкеz , то говорят, что функция
дифференцируема в точкеz . Очевидно, для дифференцируемости функции
необходимо, чтобы функцииu (x,y ) и v (x,y ) были дифференцируемы. Однако этого не достаточно для существования производной f (z ). Например, для функции w == x –iy функции u (x,y )=x

и v (x,y )=–y дифференцируемы во всех точках M(x,y ), но предел отношения
при x 0,  y 0 не существует, так как, если  y = 0,  x  0, то  w / z = 1,

если же  x = 0,  y  0, то  w /z = -1.

Единого предела не существует. Это означает, что функция

w = не имеет производную ни в одной точке z . Для существования производной от функции комплексного переменного требуются дополнительные условия. Какие именно? Ответ на этот вопрос дает следующая теорема.

Теорема. Пусть функции u (x,y ) и v (x,y ) дифферен-цируемы в точке M(x,y ). Тогда для того, чтобы функция

= u (x,y ) + iv (x,y )

имела производную в точке z = x +iy , необходимо и достаточно, чтобы выполнялись равенства

Равенства (1.38) называются условиями Коши-Римана.

Доказательство . 1) Необходимость. Пусть функция
имеет производную в точке z, то есть существует предел

=

=
.(1.39)

Предел, стоящий в правой части равенства (1.39) не зависит от того, по какому пути точка  z =  x +i  y стремится

к 0. В частности, если y = 0, x  0 (рис. 1.10), то

Если же x = 0, y  0 (рис. 1.11), то

(1.41)

Рис.1.10 Рис. 1.11

Левые части в равенствах (1.40) и (1.41) равны. Значит равны и правые части

Отсюда следует, что

Таким образом, из предположения о существовании производной f (z ) следует выполнение равенств (1.38), то есть условия Коши-Римана необходимы для существования производной f (z ).

1) Достаточность. Предположим теперь, что равенства (1.38) выполнены:

и докажем, что в этом случае функция
имеет производную в точкеz = x +iy , то есть предел (1.39)

=

существует.

Так как функции u (x,y ) и v (x,y ) дифференцируемы в точке M(x,y ), то полное приращение этих функций в точке M(x,y ) можно представить в виде

,

где  1 0,  2 0,  1 0,  2 0 при x 0, y 0.

Так как, в силу (1.38),

Следовательно,

=
,

 1 =  1 +i  1 0,  2 =  2 +i  2 0 при z = x +i y 0.

Таким образом,

Так как z  2 = x  2 +y  2 , то x / z 1, y/ z 1. Поэтому

при z  0.

Отсюда следует, что правая часть равенства (1.42) имеет предел при  z  0, следовательно, и левая часть имеет предел при  z  0, причем этот предел не зависит от того, по какому пути  z стремится к 0. Таким образом, доказано, что если в точке M(x,y ) выполнены условия (1.38), то функция
имеет производную в точкеz = x +iy , причем

.

Теорема доказана полностью.

В процессе доказательства теоремы получены две формулы (1.40) и (1.42) для производной от функции комплексного переменного

,

.

С помощью формул (1.38) можно получить еще две формулы

, (1.43)

. (1.44)

Если функция f (z ) имеет производную во всех точках области D, то говорят, что функция
дифференцируема в области D. Для этого необходимо и достаточно, чтобы условия Коши-Римана выполнялись во всех точках области D.

Пример. Проверить условия Коши-Римана для

функции e z .

Так как e z = e x+iy = e x (cosy + i siny ),

то u (x , y ) = Ree z = e x cosy , v (x , y ) = Ime z = e x siny ,

,
,

,
,

следовательно,

Условия Коши - Римана для функции e z выполнены во всех точках z. Таким образом, функция e z дифференцируема на всей плоскости комплексной переменной, причем

Точно так же доказывается дифференцируемость

функций z n , cos z , sin z , chz , shz , Lnz , и справедливость формул

(z n ) = n z n-1 , (cosz ) = -sinz , (sinz ) = cosz ,

(chz ) = shz , (shz ) = chz , (Lnz ) = 1/z .

Для функций комплексного переменного остаются в силе все правила дифференцирования функций действительного переменного. Доказательство этих правил вытекает из определения производной так же, как и для функций действительного переменного.