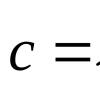§1.Неопределенный интеграл, его свойства. Правила и формулы дифференцирования. Непосредственное дифференцирование.

Основная задача интегрального исчисления обратна основной задаче дифференциального исчисления.

Пусть дана функция f (x ). Требуется найти такую функцию F (x ), что dF(x )=f " (x )dx, т.е. F" (x )= f (x ).

Функция F(x ) называется первообразной для функции f (x ). Выражение

F(x ) +C, где С – произвольная постоянная, представляет совокупность всех первообразных для функции f (x ) и называется неопределенным интегралом . Действие нахождения функции по её дифференциалу называется интегрированием .

Необходимо выучить основные свойства неопределенного интеграла и основные формулы интегрирования (табличные интегралы).

Приведем основные свойства неопределенного интеграла:

, где с =const

1. Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от каждой функции в отдельности (и наоборот).

Основные формулы интегрирования:

(1) (2) , где n

(3) (4)

(5) (6)

(7) (8)

Пример 1. Найти

Р е ш е н и е. Воспользуемся определением степени с дробным показателем и найдем интеграл

Пример 2. Найти: а) ; б)

Р е ш е н и е. а) Воспользуемся определением степени с отрицательными показателями и найти интеграл

б) По формуле (2) найдем интеграл

Пример 3. Найти:

а) В подынтегральном выражении разделим числитель на

знаменатель и воспользуемся свойством неопределенного интеграла. .

Неопределенные интегралы вычислены с использованием формул (2) и (3) таблицы интегралов.

Пример 4. Вычислить I =

Р е ш е н и е. Выполним элементарные преобразования над подынтегральной функцией:

Используя свойство 3 неопределенного интеграла, получим

Интегрирование подстановкой . Приём интегрирования функции, при котором путем замены всей подынтегральной функции или какой либо её части новым переменным приводится данный интеграл к табличному, называется интегрированием подстановкой.

Пример 5 . Вычислить

Р е ш е н и е. Выполним замену 2х =t ; тогда дифференцируя левую и правую части равенства, получим 2dx =dt и dx =

Следовательно,

При решении мы вынесли за знак интеграла сомножитель 1/2, применили формулу (7) и вернулись к прежней переменной х .

Пример 6. Вычислить .

Р е ш е н и е. Воспользуемся подстановкой х 2 + 3 = t , где t – новая переменная. Продифференцируем обе части равенства:

2xdx = dt , т.е. xdx= . Тогда интеграл имеет вид:

.

Произведя замену t = х 2 + 3 , получим

Пример 7. Найти

Р е ш е н и е. Замечаем, что sin xdx есть дифференциал функции – cosx . Полагая cosx =z, находим - sinxbх =bz , т.е. sinxbх =bz . Тогда интеграл имеет вид

Пример 8. Вычислить

Р е ш е н и е. Положим kх =t , тогда k · dx =dt , значит, dx=

Методом подстановки или методом элементарных преобразований были получены следующие табличные интегралы:

(10) (11)

(12) (13)

(14) (15)

§2. Определенный интеграл, его свойства. Формула Ньютона- Лейбница.

Пусть функция у = f (x ) разделена на отрезке от а до b на n элементарных равных частей точками a = x 0 < x 1 < x 2 < …< x n = b; выберем на каждом отрезке от х -1 до произвольную точку и обозначим через длину каждого такого отрезка.

Интегральной суммой для функции на отрезке от a до b называется сумма вида:

Определенным интегралом от функции f (x ) на отрезке от a до b называется пределинтегральной суммы при условии, что длина элементарного отрезка стремится к нулю; при этом употребляется запись .

Числа a и b называются нижним и верхним пределами интегрирования .

Таким образом,

.

Для любой функции f (x ), непрерывной на отрезке от a до b , всегда существует определенный интеграл .

Основными свойствами определенного интеграла являются:

1. Постоянный множитель можно выносить за знак определенного интеграла:

1. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждого слагаемого в отдельности:

1. При перемене местами верхнего и нижнего пределов интегрирования меняется знак определенного интеграла на противоположный:

1. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

Для вычисления определенного интеграла от функции f (x ) в том случае, когда можно найти соответствующий определенный интеграл, служит формула Ньютона-Лейбница:

т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

Все методы интегрирования рассматриваемые при изучении неопределенного интеграла, используются при вычислении определенного интеграла. Отметим, что если определенный интеграл вычисляется методом подстановки, то при переходе к новой переменной необходимо изменить и пределы интегрирования.

Пример 9. Вычислить

План

Первообразная функции и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных неопределенных интегралов. Основные методы интегрирования: непосредственное интегрирование, метод подстановки, интегрирование по частям.

Рациональные дроби. Интегрирование простейших рациональных дробей. Интегрирование рациональных дробей.

Интегрирование тригонометрических функций. Интегрирование некоторых иррациональных функций. Интегралы, не выражающиеся через элементарные функции.

Определенный интеграл. Основные свойства определенного интеграла. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Основные методы вычисления определенного интеграла (замена переменной, интегрирование по частям).

Геометрические приложения определенного интеграла. Некоторые приложения определенного интеграла в экономике.

Несобственные интегралы (интегралы с бесконечными пределами интегрирования, интегралы от неограниченных функций).

Первообразная функции и неопределенный интеграл

В интегральном исчислении основной задачей является нахождение функции y = f (x ) по ее известной производной .

Определение 1. Функция F (x ) называется первообразной функции f (x ) на интервале (a, b ), если для любого выполняется равенство: или .

Теорема 1. Любая непрерывная на отрезке [a , b ] функция f (x ) имеет на этом отрезке первообразную F (x ).

В дальнейшем будем рассматривать непрерывные на отрезке функции.

Теорема 2. Если функция F (x ) является первообразной функции f (x ) на интервале (a, b ), то множество всех первообразных задается формулой F (x )+С , где С – постоянное число.

Доказательство .

Функция F (x )+С является первообразной функции f (x ), так как .

Пусть Ф (x ) – другая, отличная от F (x ) первообразной функции f (x ), т. е. . Тогда имеем

а это означает, что

,

где С – постоянное число. Следовательно,

Определение 2. Множество всех первообразных функций F (x )+С для функции f (x ) называется неопределенным интегралом от функции f (x ) и обозначается символом .

Таким образом, по определению

(1)

В формуле (1) f (x ) называется подынтегральной функцией , f (x )dx – подынтегральным выражением , x – переменной интегрирования, знаком неопределенного интеграла .

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство кривых (каждому числовому значению С соответствует определенная кривая семейства). График каждой первообразной (кривой) называется интегральной кривой . Они не пересекаются между собой и не касаются друг друга. Через каждую точку плоскости проходит только одна интегральная кривая. Все интегральные кривые получаются одна из другой параллельным переносом вдоль оси Оy .

Основные свойства неопределенного интеграла

Рассмотрим свойства неопределенного интеграла, вытекающие из его определения.

1. Производная от неопределенного интеграла равна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению :

Доказательство .

Пусть Тогда

2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

Доказательство .

Действительно, .

3. Постоянный множитель a () можно выносить за знак неопределенного интеграла:

4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций :

5. Если F (x ) – первообразной функции f (x ), то

Доказательство .

Действительно,

6 (инвариантность формул интегрирования ). Любая формула интегрирования сохраняет свой вид, если переменную интегрирования заменить любой дифференцируемой функцией этой переменной :

где u – дифференцируемая функция .

Таблица основных неопределенных интегралов

Так как интегрирование есть действие, обратное дифференцированию, то большинство из приводимых формул может быть получено обращением соответствующих формул дифференцирования. Другими словами, таблица основных формул интегрирования получается из таблицы производных элементарных функций при обратном ее чтении (справа налево).

Приведем таблицу основных неопределенных интегралов. (Отметим, что здесь, как и в дифференциальном исчислении, буква u может означать как независимую переменную (u =x ), так и функцию от независимой переменной (u =u (x )).)

Интегралы 1–12 называются табличными .

Некоторые из приведенных выше формул таблицы интегралов, не имеющие аналога в таблице производных, проверяются дифференцированием их правых частей.

(287 г. до н. э. - 212 г. до н. э.): в сочинении «Об измерении длины окружности» рассматривается вопрос об определении площади и длины окружности круга, а в трактате «О шаре и цилиндре» - о поверхностях и объёмах некоторых тел. Для решения этих задач Архимед использовал метод исчерпывания Евдокса Книдского (ок. 408 г. до н. э. - ок. 355 г. до н. э.).

Таким образом, интегральное исчисление возникло из потребности создания общего метода нахождения площадей, объёмов и центров тяжести.

Систематическое развитие эти методы получают в XVII веке в работах Кавальери (1598-1647), Торричелли (1608-1647), П. Ферма (1601-1665), Б. Паскаля (1623-1662) и других учёных. Но их изыскания в основном имели разрозненный и утилитарный характер - решались конкретные самостоятельные задачи. В 1659 году И. Барроу (1630-1677) установил взаимосвязь между задачей о нахождении площади и задачей о нахождении касательной.

Основы классического интегрального исчисления были заложены в работах И. Ньютона (1643-1727) и Г. Лейбница (1646-1716), которые в 70-х годах XVII века отвлеклись от упомянутых частных прикладных задач и установили связь между интегральным и дифференциальным исчислением. Это позволило Ньютону, Лейбницу и их ученикам развить технику интегрирования. Своего нынешнего состояния методы интегрирования в основном достигли в работах Л. Эйлера (1707-1783). Развитие методов завершили труды М. В. Остроградского (1801-1861) и П. Л. Чебышёва (1821-1894).

Рисунок 1.1. Геометрическая интерпретация интеграла Римана.

Исторически под интегралом понимали площадь криволинейной трапеции, образованной заданной кривой и осью координат. Для нахождения этой площади отрезок a b {\displaystyle ab} разбивали на n {\displaystyle n} необязательно равных частей и строили ступенчатую фигуру (на она заштрихована). Её площадь равна

F n = y 0 d x 0 + y 1 d x 1 + … + y n − 1 d x n − 1 , {\displaystyle F_{n}=y_{0}\,dx_{0}+y_{1}\,dx_{1}+\ldots +y_{n-1}\,dx_{n-1},} (1.1)

где y i {\displaystyle y_{i}} - значение функции f (x) {\displaystyle f(x)} в i {\displaystyle i} -той точке ( i = 0 , 1 , … , n − 1 {\displaystyle i=0,\;1,\;\ldots ,\;n-1} ), а d x i = x i + 1 − x i {\displaystyle dx_{i}=x_{i+1}-x_{i}} .

Г. Лейбниц в конце XVII века обозначил предел этой суммы как

∫ y d x . {\displaystyle \int y\,dx.} (1.2)

На тот момент понятие предела ещё не сформировалось, поэтому Лейбниц ввёл новый символ для суммы бесконечного числа слагаемых ∫ {\displaystyle \int } - видоизменённую курсивную латинскую « » - первую букву лат. summa (сумма).

Слово «интеграл» происходит от лат. integralis - целостный. Это название было предложено учеником Лейбница Иоганном Бернулли (1667-1748), чтобы отличить «сумму бесконечного числа слагаемых» от обычной суммы.

В дальнейшем обозначение Лейбница усовершенствовал Ж. Фурье (1768-1830). Он явно стал указывать начальное и конечное значение x {\displaystyle x} :

∫ a b y d x {\displaystyle \int \limits _{a}^{b}y\,dx} (1.3)

введя тем самым современное обозначение определённого интеграла .

В теории определённых интегралов интегрирование рассматривается как процесс обобщения суммирования на случай бесконечно большего числа бесконечно малых выражений. Таким образом, результатом определённого интегрирования (в случае его возможности) является некое число (в обобщениях, бесконечность).

Неопределённый интеграл суть функция (точнее, семейство функций).

Интегрирование, в противоположность дифференцированию, рассматривается как искусство, что связано в первую очередь с малым количеством закономерностей, которым бы удовлетворяли все интегралы. При этом для существования интеграла, по основной теореме интегрального исчисления, необходима лишь непрерывность интегрируемой функции. Факт существования интеграла не даёт хоть какого-нибудь способа его нахождения в замкнутой форме, то есть в виде конечного числа операций над элементарными функциями . Многое в вопросе о нахождении интегралов в замкнутой форме было решено в работах Ж. Лиувилля (1809-1882). Дальнейшее развитие эта тема получила в работах, посвящённых разработке алгоритмов символьного интегрирования с использованием ЭВМ. В качестве примера можно привести алгоритм Риша .

Желая подчеркнуть обратность интегрирования по отношению к дифференцированию, некоторые авторы, используют термин «антидифференциал» и обозначают неопределённый интеграл символом D − 1 {\displaystyle D^{-1}} .

Материал из Юнциклопедии

Интегральное исчисление - это раздел математического анализа, в котором изучаются интегралы, их свойства, способы вычисления и приложения. Вместе с дифференциальным исчислением оно составляет основу аппарата математического анализа.

Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них-физическая задача определения пройденного за данное время пути по известной, но, быть может, переменной скорости движения и значительно более древняя задача вычисления площадей и объемов геометрических фигур (см. Геометрические задачи на экстремум).

Центральным в интегральном исчислении является понятие интеграла, которое, однако, имеет две различные трактовки, приводящие соответственно к понятиям неопределенного и определенного интегралов.

В дифференциальном исчислении была введена операция дифференцирования функций. Рассматриваемая в интегральном исчислении обратная к дифференцированию математическая операция называется интегрированием или, точнее, неопределенным интегрированием.

В чем же состоит эта обратная операция и в чем ее неопределенность?

Операция дифференцирования сопоставляет заданной функции F(х) ее производную F"(x)=f(x). Допустим, что мы хотим, исходя из заданной функции f(х), найти такую функцию F(х), производной которой является функция f(х), т. е. f(х) = F"(х). Такая функция называется первообразной функции f(х).

Значит, обратная дифференцированию операция - неопределенное интегрирование - состоит в отыскании первообразной данной функции.

Заметим, что, наряду с функцией F(x), первообразной для функции f(х), очевидно, будет также любая функция ℱ(х) = F(х) + С, отличающаяся от F(х) постоянным слагаемым С; ведь ℱ"(х) = F(х) = f(х).

Таким образом, в отличие от дифференцирования, сопоставлявшего функции единственную другую функцию - производную первой, неопределенное интегрирование приводит не к одной конкретной функции, а к целому набору функций, и в этом его неопределенность.

Однако степень этой неопределенности не так уж велика. Напомним, что если производная некоторой функции равна нулю во всех точках какого-то промежутка, то это функция, постоянная на рассматриваемом промежутке (на промежутках, где скорость изменения переменной величины везде равна нулю, она не меняется). Значит, если ℱ"(х) = F(х) на каком-то промежутке а<х

Итак, две первообразные одной и той же функции могут отличаться на промежутке только постоянным слагаемым.

Первообразные функции f(х) обозначают символом

где знак ∫ читается: интеграл. Это так называемый неопределенный интеграл. По доказанному, неопределенный интеграл изображает на рассматриваемом промежутке не одну конкретную функцию, а любую функцию вида

∫ f(x) dx = F(x) + C, (1)

где F(x) - какая-то первообразная функции f(х) на данном промежутке, а С-произвольная постоянная.

Например, на всей числовой оси

∫ 2х dx = х 2 + С; ∫ cos у dy = sin у + С; ∫ sin z dz = -cos z + С.

Мы здесь специально обозначили аргументы подынтегральных функций различными символами: х, у, z, чтобы обратить внимание на независимость первообразной как функции от выбора буквы, используемой для обозначения ее аргумента.

Проверка написанных равенств выполняется простым дифференцированием их правых частей, в результате которого получаются стоящие в левых частях под знаком интеграла функции 2х, cos y, sin z соответственно.

Полезно иметь в виду также следующие очевидные соотношения, непосредственно вытекающие из определений первообразной, производной, дифференциала и из соотношения (1) для неопределенного интеграла:

(∫f(x)dx)" = f(х),

d(∫f(x)dx) = f(x)dx,

∫F"(x)dx = F(x) + C,

∫dF(x) = F(x) + C.

Отыскание первообразной часто облегчают некоторые общие свойства неопределенного интеграла:

∫сf(х)dx = с∫f(х)dx (вынесение постоянного множителя);

∫(f(x) + g(х))dx = ∫f(x)dx + ∫g(х)dx (интегрирование суммы);

∫f(x)dx = F (х) + С, то

∫f(φ(t))φ"(t)dt = F(φ(t)) + C (замена переменной).

Эти соотношения также проверяются непосредственно с использованием соответствующих правил дифференцирования.

Найдем закон движения свободно падающего в пустоте тела, исходя из единственного факта, что при отсутствии воздуха ускорение д свободного падения вблизи поверхности Земли постоянно и не зависит от особенностей падающего тела. Фиксируем вертикальную координатную ось; направление на оси выберем в сторону к Земле. Пусть s(t)~ координата нашего тела в момент t. Нам известно, таким образом, что s"(t)=g и g-постоянная. Требуется найти функцию s(t) - закон движения.

Поскольку g = v"(t), где v(t) = s"(t), то, последовательно интегрируя, находим

v(t) = ∫gdt = ∫1 dt = g t + C 1 (2)

s(t) = ∫v(t)dt = ∫(g t + C 1)dt = ∫g tdt + ∫C 1 dt = g∫tdt + C 1 ∫1 dt = gt 2 /2 + C 1 t + C 2 .

Итак, мы нашли, что

s(t) = gt 2 /2 + C 1 t + C 2 , (3)

где C 1 и C 2 - какие-то постоянные. Но падающее тело подчиняется все-таки одному конкретному закону движения, в котором уже нет никакого произвола. Значит, есть еще какие-то условия, которые мы пока не использовали; они позволяют среди всех «конкурирующих» законов (3) выбрать тот, который соответствует конкретному движению. Эти условия легко указать, если разобраться в физическом смысле постоянных C 1 , и C 2 . Если сравнить крайние члены соотношения (2) при t = 0, то выяснится, что C 1 = v(0), а из (3) при t = 0 получается, что C 2 = s(0). Таким образом, математика сама напомнила нам, что искомый закон движения

s(t) = gt 2 /2 + v 0 t + s 0

вполне определится, если указать начальное положение s 0 = s(0) и начальную скорость v 0 = v(0) тела. В частности, если d 0 = 0 и s 0 = 0, получаем s(t) = gt 2 /2.

Отметим теперь, что между операцией нахождения производной (дифференцированием) и операцией отыскания первообразной (неопределенным интегрированием) имеется, кроме указанного выше, еще целый ряд принципиальных отличий. В частности, следует иметь в виду, что если производная любой комбинации элементарных функций сама выражается через элементарные функции, т. е. является элементарной функцией, то первообразная элементарной функции уже не всегда является функцией элементарной. Например, первообразная

∫((sin х)/x)dx

элементарной функции (sin х)/х (называемая интегральным синусом и обозначаемая специальным символом si(x)), как можно доказать, не выражается в элементарных функциях. Таким образом, принципиальный математический вопрос о существовании первообразной у наперед заданной функции не надо смешивать с не всегда разрешимой задачей об отыскании этой первообразной среди элементарных функций. Интегрирование часто является источником введения важных и широко используемых специальных функций, которые изучены ничуть не хуже таких «школьных» функций, как х 2 или sin х, хотя и не входят в список элементарных функций.

Наконец, отметим, что отыскание первообразной, даже когда она выражается в элементарных функциях, скорее напоминает искусство, чем канонический алгоритм вычислений, подобный алгоритму дифференцирования. По этой причине найденные первообразные наиболее часто встречающихся функций собраны в виде справочных таблиц неопределенных интегралов. Следующая микротаблица такого рода, очевидно, равносильна микротаблице производных соответствующих основных элементарных функций:

∫x n dx = 1/(n+1) x n+1 + С при n ≠ -1;

∫cos x dx = -sin x + С;

∫sin x dx = -cos x + С;

∫ dx/cos 2 x = tg x + С;

∫dx/sin 2 x = -ctg x + C.

Мы, пока говорили об обращении операции дифференцирования, пришли в этой связи к понятиям первообразной, неопределенного интеграла и дали первоначальное определение этих понятий.

Теперь укажем иной, куда более древний подход к интегралу, который послужил основным первоначальным источником интетрального исчисления и привел к понятию определенного интеграла или интеграла в собственном смысле этого слова. Этот подход четко прослеживается уже у древнегреческого математика и астронома Евдокса Книд-ского (примерно 408-355 до н.э.) и Архимеда, т.е. он возник задолго до появления дифференциального исчисления и операции дифференцирования.

Вопрос, который рассматривали Евдокс и Архимед, создав при его решении «метод исчерпывания», предвосхитивший понятие интеграла,-это вопрос о вычислении площади криволинейной фигуры. Ниже мы рассмотрим этот вопрос, а пока поставим, вслед за И. Ньютоном, следующую задачу: по известной в любой момент t из промежутка времени a≤t≤b скорости v(t) тела найти величину перемещения тела за этот промежуток времени.

Если бы был известен закон движения, т.е. зависимость координаты тела от времени, то ответ, очевидно, выражался бы разностью s(b) - s(а). Более того, если бы мы знали какую-либо первообразную s̃(0) функции v(t) на промежутке [а;b] то, поскольку s̃(t) = s(t) + С, где С - постоянная, можно было бы найти искомую величину перемещения в виде разности s̃(b) - s(а), которая совпадает с разностью s (b) - s (я). Это очень полезное наблюдение, однако если первообразную данной функции v(t) указать не удается, то действовать приходится совсем иначе.

Будем рассуждать следующим образом.

Если промежуток [а;b] отдельными моментами t 0 , t 1 , ..., t n , такими, что а = t 0 < t 1 < ... < t n = b, разбить на очень мелкие временные промежутки , i = 1, 2, ..., n, то на каждом из этих коротких промежутков скорость v(t) тела не успевает заметно измениться. Фиксировав произвольно момент τ i ∈ , можно таким образом приближенно считать, что на промежутке времени движение происходит с постоянной скоростью v(τ i). В таком случае для величины пути, пройденного за промежуток времени получаем приближенное значение v(τ i) ∆t i , где ∆t i = t i - t i-1 . Складывая эти величины, получаем приближенное значение

v(τ 1) ∆t 1 + v(τ 2) ∆t 2 + ... + v(τ n) ∆t n (4)

для всего перемещения на промежутке .

Найденное приближенное значение тем точнее, чем более мелкое разбиение промежутка мы произведем, т.е. чем меньше будет величина ∆ наибольшего из промежутков , на которые разбит промежуток .

Значит, искомая нами величина перемещения есть предел

lim ∆→0 ∑ n i=1 v(τ i) ∆t i (5)

сумм вида (4), когда величина ∆ стремится к нулю.

Суммы специального вида (4) называются интегральными суммами для функции v(t) на промежутке , а их предел (5), получаемый при неограниченном мельчании разбиений, называется интегралом (или определенным интегралом) от функции v(t) на промежутке . Интеграл обозначается символом

в котором числа а, b называются пределами интегрирования, причем а-нижним, а b-верхним пределом интегрирования; функция v(t), стоящая под знаком ∫ интеграла, называется подынтегральной функцией; v(t)dt - подынтегральным выражением; t-переменной интегрирования.

Итак, по определению,

∫ a b v(t)dt = lim ∆→0 ∑ n i=1 v(τ i) ∆t i . (6)

Значит, искомая величина перемещения тела за временной промежуток при известной скорости v(t) движения выражается интегралом (6) от функции v(t) по промежутку .

Сопоставляя этот результат с тем, который на языке первообразной был указан в начале рассмотрения этого примера, приходим к знаменитому соотношению:

∫ a b v(t)dt = s(b)-s(a), (7)

если v(t) = s"(t). Равенство (7) называется формулой Ньютона-Лейбница. В левой его части стоит понимаемый как предел (6) интеграл, а в правой-разность значений (в концах b и a промежутка интегрирования) функции s(t), первообразной подынтегральной функции v(t). Таким образом, формула Ньютона-Лейбница связывает интеграл (6) и первообразную. Этой формулой можно, следовательно, пользоваться в двух противоположных направлениях: вычислять интеграл, найдя первообразную, или получать приращение первообразной, найдя из соотношения (6) интеграл. Мы увидим ниже, что оба эти направления использования формулы Ньютона-Лейбница весьма важны.

Интеграл (6) и формула (7) в принципе решают поставленную в нашем примере задачу. Так, если v(t) = gt (как это имеет место в случае свободного падения, начинающегося из состояния покоя, т.е. с v(0) = 0), то, найдя первообразную s(t) = gt 2 /2 + С функции v(t) = g t по формуле (7), получаем величину

∫ a b gt dt = gb 2 /2 - ga 2 /2

перемещения за время, прошедшее от момента a до момента b.

На основе разобранной только что физической задачи, приведшей нас к интегралу и формуле Ньютона-Лейбница, обобщая сделанные наблюдения, можно теперь сказать, что если на некотором промежутке а ≤ х ≤ b задана функция f(х), то, разбивая промежуток [а;b] точками а = х 0 < x 1 < ... < х n = b, составляя интегральные суммы

f(ξ 1) ∆x 1 + f(ξ 2) ∆x 2 + ... + f(ξ n) ∆x n , (4")

где ξ i ∈ , ∆x i = x i - x i-1 , и переходя к пределу при ∆→0, где ∆ = max {∆x 1 , ∆x 2 , ..., ∆x n }, мы получаем по определению интеграл

∫ a b f(x) dx = lim ∆→0 ∑ n i=1 f(ξ i) ∆x i (6")

от функции f(х) по промежутку . Если при этом F"(x)=f(x) на , т.е. F(x) - первообразная функции f(х) на промежутке , то имеет место формула Ньютона-Лейбница:

∫ a b F(x) dx = F(b) - F(а). (7")

Итак, определены важнейшие понятия интегрального исчисления и получена формула Ньютона-Лейбница, связывающая интегрирование и дифференцирование.

Подобно тому как в дифференциальном исчислении к понятию производной вела не только задача определения мгновенной скорости движения, но и задача проведения касательной, так в интегральном исчислении к понятию интеграла приводит не только физическая задача определения пройденного пути по заданной скорости движения, но и многие другие задачи, и в их числе древние геометрические задачи о вычислении площадей и объемов.

Пусть требуется найти площадь S изображенной на рис. 1 фигуры aABb (называемой криволинейной трапецией), верхняя «сторона» АВ которой есть график заданной на отрезке функции у =f(х). Точками а = х 0 < х 1 < ... < х n = b разобьем отрезок на мелкие отрезки , в каждом из которых фиксируем некоторую точку ξ i ∈ . Площадь узкой криволинейной трапеции, лежащей над отрезком , заменим приближенно площадью f(ξ i)(x i-1 - x i) = f(ξ i)∆x i соответствующего прямоугольника с основанием и высотой f(ξ i). В таком случае приближенное значение площади S всей фигуры aABb даст знакомая нам интегральная сумма ∑ n i=1 f(ξ i) ∆x i , а точное значение искомой площади S получится как предел таких сумм, когда длина ∆ наибольшего из отрезков разбиения стремится к нулю. Таким образом, получаем:

∫ a b f(x) dx. (8)

Попробуем теперь вслед за Архимедом выяснить, в каком отношении парабола у = х 2 делит площадь изображенного на рис. 2 единичного квадрата. Для этого попросту вычислим, исходя из формулы (8), площадь S нижнего параболического треугольника. В нашем случае = и f(х) = х 2 . Нам известна первообразная F(x) = x 3 /3 функции f(х) = х 2 , значит, можно воспользоваться формулой (7") Ньютона-Лейбница и без труда получить

S = ∫ 0 1 х 2 dx = 1/3 1 3 - 1/3 0 3 = 1/3.

Следовательно, парабола делит площадь квадрата в отношении 2:1.

При обращении с интегралами, особенно применяя формулу Ньютона-Лейбница, можно пользоваться общими свойствами неопределенного интеграла, которые названы в начале статьи. В частности, правило замены переменной в неопределенном интеграле при условии, что а = φ(α), b = φ(β), с учетом формулы Ньютона-Лейбница позволяет заключить, что

∫ a b f(x) dx = F(b) - F(a) = F(φ(β)) - F(φ(α)) = ∫ α β f(φ(t))φ"(t) dt,

и таким образом, получается очень полезная формула замены переменной в определенном интеграле:

∫ a b f(x) dx = ∫ α β f(φ(t))φ"(t) dt (9)

С помощью интегралов вычисляют также объемы тел. Если изображенную на рис. 1 криволинейную трапецию aABb вращать вокруг оси Ох, то получится тело вращения, которое приближенно можно считать составленным из узких цилиндров (рис. 3), полученных при вращении соответствующих прямоугольников. Сохраняя прежние обозначения, записываем объем каждого из этих цилиндров в виде πf 2 ξ i ∆x i , (произведение площади πf 2 ξ i основания на высоту ∆x i). Сумма πf 2 ξ 1 ∆x 1 + πf 2 ξ 2 ∆x 2 + ... + πf 2 ξ n ∆x n дает приближенное значение объема V рассматриваемого тела вращения. Точное значение V получится как предел таких сумм при ∆→0. Значит,

V = π∫ a b f 2 (x) dx. (10)

В частности, чтобы вычислить объем изображенного на рис. 4 конуса, достаточно положить в формуле (10) а = 0, b = h и f(х) = kх, где k - угловой коэффициент вращаемой прямой. Найдя первообразную k 2 x 3 /3 функции f 2 (x) = k 2 x 2 и воспользовавшись формулой Ньютона-Лейбница, получаем

V = π∫ 0 h k 2 x 2 dx = π(k 2 h 3 /3 - k 2 0 3 /3)

= π(kh) 2 h/3 = Sh/3,

где S = π(kh) 2 площадь круга, лежащего в основании конуса.

В разобранных примерах мы исчерпывали геометрическую фигуру такими фигурами, площади или объемы которых могли вычислить, а затем делали предельный переход. Этот прием, идущий от Евдокса и развитый Архимедом, называется методом исчерпывания. Это наиболее распространенный метод рассуждений в большинстве применений интеграла.

В качестве еще одного примера рассмотрим вполне конкретный «космический» вопрос.

Мы хотим вычислить скорость V, до которой нужно разогнать тело (ракету), чтобы затем оно, удаляясь по инерции от планеты вдоль радиуса, уже никогда не было возвращено притяжением планеты назад. Эта скорость называется второй космической, в отличие от первой космической, которую должен иметь спутник, выходящий на орбиту у поверхности планеты.

Пусть m-масса тела, М-масса планеты. Кинетической энергии mv 2 /2, которой следует наделить тело для выхода из поля притяжения планеты, должно хватить, чтобы совершить работу против силы тяготения. Величина этой силы на расстоянии r от центра планеты по открытому Ньютоном закону всемирного тяготения равна

где G - гравитационная постоянная. Таким образом, эта сила меняется, причем ослабевает по мере удаления от планеты.

Вычислим работу A R R 0 , которую нужно совершить, чтобы тело, находящееся на высоте R 0 (считая от центра планеты), поднять на высоту R.

Если бы сила была постоянна, то мы просто умножили бы ее величину на длину R - R 0 пройденного вдоль направления ее действия пути и нашли бы совершенную работу. Но сила меняется, поэтому мы разобьем весь промежуток точками R 0 = r 0 < 1 < ... < r n = R на маленькие промежутки, в пределах которых изменением силы можно пренебречь; найдем приближенно элементарные работы

G mM/r i 2 (r i - r i-1) = G mM/r i 2 ∆r i

на каждом из промежутков ; сложив элементарные работы

G mM/r 1 2 ∆r 1 + G mM/r 2 2 ∆r 2 + ... + G mM/r n 2 ∆r n

получим приближенное значение искомой работы A R R 0 на промежутке , а точнее значение A R R 0 выражается, таким образом, следующим интегралом:

A R R 0 = ∫ R R 0 G mM/r 2 dr

в котором роль переменной интегрирования играет r. Величины G, m, M постоянны, а функция r -2 имеет первообразную -r -1 , зная которую по формуле Ньютона-Лейбница находим

A R R 0 = GmM (1/R 0 - 1/R).

Если R увеличивать неограниченно, т.е., как говорят, удалять тело на бесконечность, то, переходя к пределу при R → ∞, получаем

A ∞ R 0 = GmM/R 0 ,

где ∞-символ, читаемый «бесконечность». Если в последней формуле считать, что R 0 -радиус планеты, то A ∞ R 0 будет работой, которую надо совершить против сил тяготения, чтобы тело с поверхности планеты ушло в бесконечность.

Полученное для A ∞ R 0 выражение можно упростить, если вспомнить другой закон Ньютона F = ma, связывающий силу F и вызванное ею ускорение a тела массы m. Свободно падающее на планету тело у ее поверхности имеет ускорение а = g, вызванное силой притяжения

где R 0 - радиус планеты. Значит,

GmM/R 0 2 = mg, откуда следует, что

GmM/R 0 2 = g и, значит A ∞ R 0 = mGR 0 .

Это и есть формула для подсчета работы, необходимой для выхода из поля притяжения планеты. Для «ухода» с планеты по инерции нужно иметь вертикальную скорость v, при которой кинетическая энергия mv 2 /2 тела не меньше или, по крайней мере, равна работе затрачиваемой на преодоление притяжения планеты.

Таким образом, вторая космическая скорость, получаемая из равенства mv 2 /2 = mgR 0 , выражается в виде

В частности, для Земли g ≈ 10 м/с 2 , R 0 ≈ 6 400 000 м, поэтому v ≈ 8000 √2 м/с, или v ≈ 11,2 км/с.

Во всех разобранных до сих пор примерах мы использовали первообразную, чтобы по формуле (7") Ньютона Лейбница вычислить интересовавший нас интеграл. Но та же формула Ньютона-Лейбница наводит на мысль использовать сам интеграл для нахождения первообразной или, по крайней мере, для выяснения принципиального вопроса о ее существовании. Этого вопроса мы уже коснулись в разделе, посвященном первообразной и неопределенному интегралу. Теперь мы рассмотрим его несколько внимательнее.

Пусть на отрезке задана функция f, график которой изображен линией AB на рис. 5. Мы знаем, что площадь всей криволинейной трапеции aABb выражается интегралом (8). Обозначим через ℱ(х) площадь той ее части, которая лежит над отрезком [а;х].

ℱ(x)=∫ a x f(x)dt. (11)

Здесь мы обозначили переменную интегрирования через t, чтобы не путать ее с х, являющимся в нашем случае верхним пределом интегрирования.

Величина ℱ(x), очевидно, зависит от точки x∈.

Покажем, что ℱ(x) - первообразная функции f(х) на отрезке , т.е. ℱ"(x)=f(х) при x∈. В самом деле, как видно из рис. 5,

ℱ(x+h) - ℱ(x) ≈ f(x) h,

что равносильно приближенному равенству

(ℱ(x+h) - ℱ(x))/h ≈ f(x)

При уменьшении величины h точность этого соотношения только улучшается, поэтому

lim h→0 (ℱ(x+h) - ℱ(x))/h = f(x)

и, значит,

Таким образом, интеграл (11) с переменным верхним пределом х дает нам первообразную функции f(х). Среди всех прочих первообразных функции f(х) на отрезке эта первообразная выделяется очевидным условием ℱ(a) = 0. Поскольку интеграл, согласно его определению (6"), можно вычислить с любой наперед заданной точностью, то и значение ℱ(х) первообразной (11) функции f(х) в любой точке x∈ можно найти сколь угодно точно, даже не интересуясь при этом аналитической записью ℱ(х) или вопросом о том, является ли ℱ(х) элементарной функцией.

Существуют простые и очень эффективные численные методы интегрирования - это так называемые квадратурные формулы. Они позволяют на электронных вычислительных машинах за доли секунды получать значения определенных интегралов. Это обстоятельство делает формулу (11) средством отыскания первообразной. Например, современные подводные лодки порой месяцами находятся на большой глубине и перемещаются на огромные расстояния; не имея никакой связи с внешним миром, они тем не менее выходят в точно заданный квадрат. Навигационное оборудование, которое позволяет определять координаты лодки в любой момент, является технической реализацией формулы (11) и основано на таком физическом принципе. Находясь в закрытом движущемся помещении (хорошо звукоизолированном мягком вагоне, самолете и т.д.), мы не ощущаем скорости движения, но зато определенно чувствуем изменение скорости-ускорение. Оно положительно при увеличении скорости, когда масса вдавливает вас в самолетное кресло, и отрицательно при торможении, когда вам могут пригодиться даже пристяжные ремни. Поскольку между ускорением а массы m и вызывающей его силой F имеется прямая пропорциональная зависимость F = mа, величину а укорения можно объективно измерять, закрепив массу m на свободном конце пружинки, расположенной вдоль направления движения, и соединив жестко второй ее конец, например, с задней стенкой движущегося помещения. Если растяжение и сжатие пружины пропорционально действующей на нее силе, то по величине отклонения массы m от положения равновесия можно узнавать величину a(t) ускорения, происходящего в данном направлении в любой момент времени t.

Если движение начиналось с нулевой начальной скоростью, то, зная a(t), можно по формуле (11) найти сначала скорость v(t) движения, а зная v(t), найти и перемещение s(t) в этом направлении к моменту и поскольку

v(t) = ∫ 0 t a(u) du, a s(t) = ∫ 0 t v(u) du.

Обработка показаний приборов и вычисление этих интегралов выполняется электронной вычислительной машиной. Если есть три датчика ускорения, удерживаемых (например, гироскопами) в трех взаимно перпендикулярных направлениях, то вы можете в любой момент знать ваше перемещение по каждому из указанных направлений и тем самым определить все три ваши координаты в некоторой системе координат, началом которой является точка старта-база, аэродром, космодром.

Понятие интеграл непосредственно связано с интегральным исчислением – разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления. Вместе с дифференциальным исчислением интегральное исчисление составляет основу математического анализа.

Истоки интегрального исчисления относятся к античному периоду развития математики и берут начало от метода исчерпывания, разработанного математиками Древней Греции.

Метод исчерпывания это набор правил для вычисления площадей и объёмов, разработка которых приписывается Евдоксу Книдскому. Дальнейшее развитие метод получил в работах Евклида, а особым искусством и разнообразием применения метода исчерпывания славился Архимед.

Типичная схема доказательств методом исчерпывания выглядела следующим образом. Для определения величины A строилась некоторая последовательность величин С1, С2, …, Сn, … такая, что

Предполагалось также известным такое B, что

и что для любого целого K можно найти достаточно большое n, удовлетворяющее условию:

Где D – постоянно. После громоздких рассуждений из последнего выражения удавалось получить:

Как видно из приведённой схемы метод был основан на аппроксимации рассматриваемых объектов ступенчатыми фигурами или телами, составленными из простейших фигур или пространственных тел (прямоугольников, параллелепипедов, цилиндров и т.п., обозначенных последовательностью С1, С2, …, Сn, …). В этом смысле метод исчерпывания можно рассматривать как античный интегральный метод.

Кризис и упадок древнего мира привёл к забвению многих научных достижений. О методе исчерпывания вспомнили лишь в XVII веке. Это было связано с именами Исаака Ньютона, Готфрида Лейбница, Леонарда Эйлера и ряда других выдающихся учёных, положивших основу современного математического анализа.

В конце XVII и в XVIII веке все возрастающие запросы практики и других наук побуждали ученых максимально расширять область и методы исследований математики. Понятия бесконечности, движения и функциональной зависимости выдвигаются на первое место, становятся основой новых методов математики.

В конце XVII и в XVIII веке в математике и механике были получены классические результаты фундаментального значения. Основным здесь было развитие дифференциального и интегрального исчисления, теории дифференциальных уравнений, вариационного исчисления и аналитической механики.

Основные понятия и теория интегрального и дифференциального исчислений, прежде всего связь операций дифференцирования и интегрирования, а также их применения к решению прикладных задач были разработаны в конце XVII века, но основывались на идеях, сформулированных в начале XVII веке великим математиком и астрономом Иоганом Кеплером.

В ноябре 1613 года королевский математик и астролог австрийского двора И. Кеплер праздновал свадьбу. Готовясь к ней, он приобрёл несколько бочек виноградного вина. При покупке Кеплер был поражён тем, что продавец определял вместимость бочки, производя одно единственное действие - измеряя расстояние от наливного отверстия до самой дальней от него точки днища. Ведь такое измерение совершенно не учитывало форму бочки! Кеплер сразу увидел, что перед ним интереснейшая математическая задача - по нескольким измерениям вычислить вместимость бочки. Размышляя над этой задачей, он нашёл формулы не только для объёма бочек, но и для объёма самых различных тел: лимона, яблока, айвы и даже турецкой чалмы. Для каждого из тел Кеплеру приходилось создавать новые, зачастую очень хитроумные методы, что было крайне неудобно. Попытка найти достаточно общие, а, главное, простые методы решения подобных задач и привела к возникновению современного интегрального счисления. Но это уже была заслуга совсем другого математика.

Трудно найти другое имя, которое оказало бы столь сильное влияние на историю мировой науки и культуры, как Исаак Ньютон. Известный математик и историк науки Б. Л. Ван-дер-Варден пишет в своей книге “Пробуждающаяся наука”: “Каждый естествоиспытатель безусловно согласится, что механика Ньютона есть основа современной физики. Каждый астроном знает, что современная астрономия начинается с Кеплера и Ньютона. И каждый математик знает, что самим значительным н наиболее важным для физики отделом современной математики является анализ, в основе которого лежат дифференциальное и интегральное исчисления Ньютона. Следовательно, труды Ньютона являются основой огромной части точных наук нашего времени”. И не только наук: “Математика и техника влияют даже на нашу духовную жизнь, и настолько. что мы редко можем представить это себе полностью. Вслед за необычайным взлётом, которое пережило и XVII веке естествознание, последовал неизбежно рационализм XVIII века, обожествление разума, упадок религии... Кто отдает себе отчет в том, - спрашивает автор, - что с исторической точки зрения Ньютон является самой значительной фигурой XVII века?”

Исаак Ньютон родился в 1643 году. Мальчик посещал сначала сельскую школу, а в двенадцать лет его отправили учиться в ближайший город. Директор школы обратил внимание на способного мальчика и уговорил мать Ньютона отправить сына учиться в Кембриджский университет. Ньютон был принят туда в качестве бедного студента, обязанного прислуживать бакалаврам, магистрам и студентам старших курсов.

Кафедру математике в Кембридже занимал тогда молодой блестящий учёный Исаак Барроу. Он скоро стал не только учителем, но и другом Ньютона, а спустя несколько лет уступил своему великому ученику кафедру математики. К этому времени Ньютон получил уже степени бакалавра и магистра. В 1665-1667 годах Ньютон начал работать над созданием математического аппарата, с помощью которого можно было бы исследовать и выражать законы физики. Ньютон первый построил дифференциальное и интегральное исчисления (он назвал его методом флюксий). Это сразу позволило решать самые разнообразные, математические и физические, задачи. До Ньютона многие функции определялись только геометрически, так что к ним невозможно было применять алгебру и новое исчисление флюксий. Ньютон нашел новый общий метод аналитического представления функции - он ввел в математику и начал систематически применять бесконечные ряды.

Поясним эту идею Ньютона. Известно, что любое действительное число можно представить десятичной дробью - конечной или бесконечной. Так. например:

Это значит, что любое число a можно представить в виде:

где N - целая часть, а a1, a2, ... an, ... могут принимать одно из значений 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. По аналогии с таким представлением чисел Ньютон предположил, что любая функция от x, например , может быть представлена как бесконечный многочлен или ряд, расположенный уже не по степеням , а по степеням x:

где a1, a2, ... an, ...- коэффициенты, которые каждый раз должны быть определены. Примером такого ряда может служить известная нам геометрическая прогрессия:

Представление функции с помощью ряда очень удобно. С помощью рядов, как писал Ньютон, “удается преодолеть трудности, в другом виде представляющиеся почти неодолимыми”.

Одновременно с Ньютоном к аналогичным идеям пришёл другой выдающийся учёный - Готфрид Вильгельм Лейбниц.

Готфрид Вильгельм Лейбниц родился в Германии в г. Лейпциге в 1646 г. Любознательный мальчик уже 6 лет вел интересные беседы по истории со своим отцом, профессором Лейпцигского университета. К 12 годам он хорошо изучил латинский язык и увлёкся древнегреческим. Особенно его интересовали древние философы, и он мог подолгу размышлять о философских теориях Аристотеля или Демокрита. В 15 лет Лейбниц поступает и Лейпцигский университет, где усердно изучает право и философию. Он очень много читает, среди его любимых книг - книги Р. Декарта, Г. Галилея, II. Кеплера и Д. Кампанеллы.

Свои колоссальные знания но математике Лейбниц приобрел самоучкой. Через три года, окончив университет, Лейбниц покинул Лейпциг. Он был обижен отказом ученого совета университета присвоить ому степень доктора прав. Отказ объяснили тем. что Лейбниц был... слишком молод!

Началась жизнь, полная напряженного труда и многочисленных путешествии. Легко себе представить, как неудобны были путешествовать в неуклюжих каретах по тряским дорогам Европы тех времен. Лейбниц умел не терять времени даром - много удачных мыслей пришло ему и голову именно во время этих продолжительных поездок. Лейбниц отличался исключительной способностью быстро “входить” и задачу и решать ее наиболее общим способом. Размышляя над философскими и математическими вопросами, Лейбниц убедился, что самым надежным средством искать и находить истину в науке может стать математика. Всю спою сознательную жизнь он стремился выразить законы мышления, человеческую способность думать и виде математического исчисления. Для этого необходимо, учил Лейбниц, уметь обозначать любые понятия или идеи определенными символами, комбинируя их в особые формулы, и сводить правила мышления к правилам в вычислениях но этим символическим формулам. Заменяя oбычные слова четко определенными символами, Лейбниц стремился избавить наши рассуждения от всякой неопределенности и возможности ошибиться самому или вводить в заблуждение других. Если, мечтал Лейбниц. между людьми возникнут разногласия, то решаться они будут не в длинных и утомительных спорах. а так, как решаются задачи или доказываются теоремы. Спорщики возьмут в руки перья и, сказав: “Начнем вычислять” - примутся за расчеты.

Как уже отмечалось, Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Об этом свойстве хороню знал и Ньютон. Но только Лейбниц увидел здесь ту замечательную возможность, которую открывает применение символического метода.

Любой человек, изучив небольшое число правил действия с символами, обозначающими операции дифференцирования и интегрирования, становится обладателем мощного математического метода. В наше время такие символы операций называют операторами. Операторы дифференцирования d() и интегрирования действуют на функции, “перерабатывая” их в другие, точно вычисляемые функции. Лейбниц разрабатывает особую алгебру действий с этими операторами. Он доказывает, что обычное число а можно выносить за знак оператора:

Одинаковые операторы можно выносить за скобку:

Сокращенно все перечисленные свойства можно выразить соотношением:

где: a и b - числа.

Операторы. которые обладают таким свойством. называются линейными. Теория линейных операторов, которую с таким успехом начал развивать, Лейбниц,. в современной математике является хорошо разработанной и полезной в приложениях теорией.

Многократное применение операторов можно принимать как степень оператора, например, для d():

То, что основные операторы математического анализа являются взаимно обратными Лейбниц подчёркивал своей символикой, утверждая, что в d(x) и также взаимно обратны, как степени и корни в обычном исчислении. Употребляя так же обозначение, аналогичное обозначению a-1 числа, обратного a, причём произведение a×a-1=1. Обозначая операторы или наоборот:

и понимая под их произведением последовательное их применение, имеем:

т. е. произведение есть “единица”, не меняющая функцию.

Однако, в подходе Ньютона-Лейбница крылось серьёзное противоречие.

Лейбниц и его последователи - братья Бернулли, Лопиталь и другие - трактовали дифференциалы как бесконечно малые разности обычных конечных величин, как тогда говорили - “реальных” величин “низшей” математики. Поэтому они обращались с теми и другими одинаково и в исчислении применяли к первым те же приемы, которые справедливы при действиях со вторыми. Вместе с тем выяснилось, что таким образом трактуемым бесконечно малым присуще свойство, противоречащее одному основному свойству основных конечных величин: если А - конечная величина, а a - бесконечно малая, то, чтобы результат исчисления получался совершенно точным, оказалось необходимым проводить вычисления в предположении, что А+a=А.

Дифференциальное исчисление, значение которого для развития науки и техники было вне сомнений, оказалось в парадоксальном положении: чтобы его методами получить точный результат, надо было исходить из ошибочного утверждения.

Ньютон пытался обосновать дифференциальное исчисление на законах механики и понятии предела. Но ему не удалось освободить свое исчисление флюксий от недостатков, присущих дифференциальному исчислению Лейбница. В практике вычисления Ньютон, как и Лейбниц, применял принцип отбрасывания бесконечно малых.

Такая непоследовательность позволила назвать дифференциальное исчисление Лейбница–Ньютона мистическим. Этим в первую очередь подчеркивалось, что Лейбниц и Ньютон вводили в дифференциальное исчисление бесконечно малые величины метафизически, сразу полагая их существующими, без выяснения их возникновения и развития и без анализа природы их специфических свойств.

Попытки построить анализ бесконечно малых и теорию рядов в полном соответствии с основными понятиями и истинами “низшей” математики с самого начала к успешным результатам не привели. Поэтому Лейбниц и его последователи пытались оправдать принципы анализа бесконечно малых путем сравнения бесконечно малой с песчинкой, которой можно пренебречь при вычислении высоты горы, посредством ссылок на вероятность и т. п.

Другая попытка была предпринята в конце XVIII века. Известный немецкий математик Вессель предложил оставить анализ бесконечно малых в анализе в качестве “полезных вспомогательных функций”. Однако, такая трактовка широкого распространения не получила - математики знали механическое и геометрическое истолкование dx и dy.

Примерно с последней четверти XVIII века область приложений математического анализа начинает значительно перекрывать границы его обычного приложения в механике и геометрии. Ещё быстрее развертывается этот процесс в первой четверти XIX века.

Математики пытались сначала решать новые задачи методами, разработанными классиками XVIII века - Эйлером, Даламбером, Лагранжем и другими. Однако, вскоре выяснилось, что методы классиков недостаточны, что надо развивать новые, более общие и сильные методы. Выяснилось также, что недостаточность методов классиков нередко связана с узостью трактовки основных понятий, с “изгоняемым” понятием о бесконечно малом, с “исключениями”, которые раньше оставались в тени.

Поясним сказанное одним примером.

Ньютон и Лейбниц разработали две трактовки понятия обычного определенного интеграла.

Ньютон трактовал определенный интеграл как разность соответствующих значений первообразной функции:

,

где F`(x)=f(x).

Для Лейбница определенный интеграл был суммой всех бесконечно малых дифференциалов.

.

Первая трактовка отвечала технике вычисления определенных интегралов при помощи первообразной подынтегральной функции, вторая - потому, что в приложениях определенный интеграл появлялся как предел известного вида суммы (интегральной суммы).

Примерно до последней четверти XVIII века первая трактовка понятия определенного интеграла занимала господствующее положение. Этому способствовали два обстоятельства.

К началу XVIII века были установлены правила дифференцирования всех элементарных функций и началась успешная разработка методов нахождения их первообразных (рациональных, отдельных классов иррациональных и трансцендентных функций). Благодаря этому точка зрения Ньютона вполне отвечала развитию эффективных алгоритмов интегрального исчисления.

Непосредственное вычисление как предела интегральной суммы столкнулось с многими трудностями. Естественно, что это обстоятельство укреплению точки зрения Лейбница не способствовало.

Истолкование обычного определенного интеграла по Лейбницу опиралось на понятие о бесконечно малых, от которого математики XVIII века хотели освободить математический анализ. Это также способствовало укреплению точки зрения Ньютона. Факт этот хорошо подтверждался тем, как Леонард Эйлер использовал понятие об интегральной сумме. Эйлер не возражал против приближенного вычисления определенных интегралов при помощи соответствующих интегральных сумм. Но рассматривать определенный интеграл как предел интегральной суммы он не мог. В этом случае все слагаемые интегральной суммы становились бесконечно малыми, т. е., с точки зрения Эйлера, были нулями.

Историческая справка. В 1963 г. 23-летний Пауль Эйлер окончил курс теологии в Базельском университете. Но учёных теологов было в те годы больше, чем требовалось, и лишь в 1701 г. он получил официальную должность священника сиротского дома в Базеле. 19 апреля 1706 г. пастор Пауль Эйлер женился на дочери священника. А 15 апреля 1707 г. у них родился сын, названный Леонардом.

Начальное обучение будущий учёный прошел дома под руководством отца, учившегося некогда математике у Якоба Бернулли. Добрый пастор готовил старшего сына к духовной карьере, однако занимался с ним и математикой – как в качестве развлечения, так и для развития логического мышления. Мальчик увлёкся математикой, стал задавать отцу вопросы один сложнее другого.

Когда у Леонардо проявился интерес к учёбе, его направили в Базельскую латинскую гимназию – под надзор бабушки.

20 октября 1720 г. 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета: отец желал, чтобы он стал священником. Но любовь к математике, блестящая память и отличная работоспособность сына изменили эти намерения и направили Леонарда по иному пути.

Став студентом, он легко усваивал учебные предметы, отдавая предпочтение математике. И немудрено, что способный мальчик вскоре обратил на себя внимание Бернулли. Он предложил юноше читать математические мемуары, а по субботам приходить к нему домой, чтобы совместно разбирать непонятное. В доме своего учителя Эйлер познакомился и подружился с сыновьями Бернулли – Николаем и Даниилом, также увлечённо занимавшимися математикой. А 8 июня 1724г. 17-летний Леонард Эйлер произнёс по- латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона - и был удостоен учёной степени магистра (в XIX в. в большинстве университетов Западной Европы ученая степень магистра была заменена степенью доктора философии).

Эйлер отличался феноменальной работоспособностью. Он просто не мог не заниматься математикой или её приложениями. В 1735 г. Академия получила задание выполнить срочное и очень громоздкое астрономическое вычисление. Группа академиков просила на эту работу три месяца, а Эйлер взялся выполнить работу за 3 дня – и справился самостоятельно. Однако перенапряжение не прошло бесследно: он заболел и потерял зрение на правый глаз. Однако учёный отнёсся к несчастью с величайшим спокойствием: “Теперь я меньше буду отвлекаться от занятий математикой”, - философски заметил он.

До этого времени Эйлер был известен лишь узкому кругу учёных. Но двухтомное сочинение “ Механика, или наука о движении, в аналитическом изложении ”, изданное в 1736 г., принесло ему мировую славу. Эйлер блестяще применил методы математического анализа к решению проблем движения в пустоте и в сопротивляющейся среде. “Тот, кто имеет достаточные навыки в анализе, сможет всё увидеть с необычайной лёгкостью и без всякой помощи прочитает работу полностью”, - заканчивает Эйлер своё предисловие к книге.

Дух времени требовал аналитического пути развития точных наук, применения дифференциального и интегрального исчисления для описания физических явлений. Этот путь и начал прокладывать Леонард Эйлер.

Конечно, и до последней четверти XVIII века концепция Ньютона сталкивалась с трудностями. В этот период встречались элементарные функции, первообразные которых не могут быть выражены через элементарные функции. Знали математики и некоторые несобственные интегралы, в том числе и расходящиеся. Но такого рода факты были единичными и установившейся эффективной концепции интеграла нарушить не могли. Иным оказалось положение в последней четверти XVIII и особенно в начале XIX века.

С 70-х годов XVIII века решение задач аналитической механики, физики и других дисциплин потребовало значительное развитие понятия определенного интеграла. Особое значение приобретают двойные и тройные интегралы (Эйлер, Лагранж, Лаплас и др.).

Это было время, когда великие идеи Ньютона и Лейбница были опубликованы сравнительно недавно и современный математический анализ только создавался. Мощные методы, которые принесли с собой эти идеи, находили применение во всех отраслях точного знания. Применение это шло рука об руку с развитием самого анализа, часто указывая пути и направления, по которым должно развиваться новое исчисление. Это была, пожалуй, единственная по своей интенсивности эпоха математического творчества, и Эйлер был один из немногих по своей продуктивности творцов. Его "Введение в анализ бесконечно малых", "Основания дифференциального исчисления" и "Основания интегрального исчисления" были первыми трактатами, в которых уже обширный, но разрозненный материал нового анализа был объединен в цельную науку. В них был выработан тот скелет современного анализа, который сохранился и до нашего времени.

Разработка приемов вычисления двойных и тройных интегралов показала, что вычислять эти интегралы так, как вычисляли обычный определенный интеграл - при помощи неопределенного, очень трудно или даже невозможно. Поэтому математики вынуждены были сохранять концепцию Ньютона только на словах, а на деле, при решении задач точных наук, стали на путь Лейбница. Они вычисляли соответствующие интегральные суммы (в прямоугольных, цилиндрических и сферических координатах) и находили их пределы.

Короче говоря, разработка способов вычисления новых видов определенного интеграла показала, что обыкновенный, двойной и т. д. определенный интегралы должны быть обоснованы сами по себе независимо от понятия неопределенного интеграла. Но каждое слагаемое любой интегральной суммы является бесконечно малой величиной. Тем самым не только ставился вопрос о легализации ранее “изгоняемого” понятия бесконечно малого, но и о раскрытии его реального содержания и о соответствующем его использовании. Как уже указывалось, чтобы всё это сделать надо было преодолеть - обобщить, развить традиционное (Эйлерово) толкование функции и понятия предела.

В связи с этим возник вопрос о существовании пределов интегральных сумм, слагаемые которых были бы бесконечно малыми. В первой четверти XIX века понятие бесконечно малой оказалось необходимым и для изучения и сопоставления свойств непрерывных и разрывных функций. Получение основополагающих результатов связано здесь с именем Коши. “Между многими понятиями, - указывал Коши, - тесно связанными со свойствами бесконечно малых, следует поместить понятие о непрерывности и прерывности функций”. Тут же Коши дает истолкование непрерывности функции, которое более чем ясно подтверждает ясность этого его утверждения.

Новая постановка задач обоснования математического анализа ясно показывала, что дело не только в признании и применении бесконечно малых - это делали и раньше! - но прежде всего в научном истолковании их содержания и обоснованном на этом использовании их в алгоритмах математического анализа. Однако, чтобы это сделать надо было преодолеть господствовавшее в XVIII веке узкое толкование понятия предела, разработать общую теорию пределов.

Изучение разрывных функций и сопоставление их с функциями непрерывными заставило признать то, что ранее считалось невозможным: что предел, к которому стремиться последовательность значений функции, при стремлении аргумента в некоторой точке может оказаться отличным от значения функции в этой точке. Значит, предел не всегда является “последним” значением переменной, но во всех случаях предел есть число, к которому переменная приближается неограниченно. Следовательно, dx и dy не необходимо нули или “мистически” актуально бесконечно малые; бесконечно малая - это переменная, имеющая пределом нуль, причем факт этот с противоречиями и парадоксами не связан.

Коши преодолел и вторую ограничительную тенденцию в принятой до него трактовке понятия предела. Он признал, что переменная может приближаться к своему пределу не только монотонно, но и колеблясь, порой принимая значения, равные её пределу. Это обстоятельство придало теории Коши необходимую общность и исключительную гибкость. Мы до сих пор следуем пути, намеченному Огюстеном Луи Коши, с теми усовершенствованиями, которые были внесены во второй половине XIX века К. Вейерштрассом.

Работы Коши и Вейерштрасса завершили создание классического математического анализа, Тем самым подведя итог многовекового развития интегрального исчисления.

Список литературы

Большакова А. А. Три кризиса в развитии математики. Дипломная работа; Астрахань: АГПИ, 1996.

Детская энциклопедия для среднего и старшего возраста. Т.2; М.: Просвещение, 1965.

Математическая энциклопедия. Ред. Виноградова. Т.2; М.: Сов. Энциклопедия, 1979.

Фихтенгольц Г.М. Основы математического анализа. Т.1; М.: Наука, 1968.