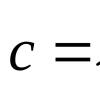Равно нулю:

Ортогональная система в случае её полноты может быть использована в качестве базиса пространства. При этом разложение любого элемента может быть вычислено по формулам: , где .

Случай, когда норма всех элементов , называется ортонормированной системой .

Ортогонализация

Любая полная линейно независимая система в конечномерном пространстве является базисом. От простого базиса, следовательно, можно перейти к ортонормированному базису.

Ортогональное разложение

При разложении векторов векторного пространства по ортонормированному базису упрощается вычисление скалярного произведения: , где и .

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое "Ортогональная система" в других словарях:

1) О … Математическая энциклопедия

- (отгреч. orthogonios прямоугольный) конечная или счётная система ф ций, принадлежащих (сепара бельному) гильбертову пространству L2(a,b)(квадратично интегрируемых ф ций) и удовлетворяющих условиям Ф ция g(x)наз. весом О. с. ф.,* означает… … Физическая энциклопедия

Система функций??n(х)?, n=1, 2,..., заданных на отрезке ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ линейное преобразование евклидова векторного пространства, сохраняющее неизменными длины или (что эквивалентно этому) скалярные произведения векторов … Большой Энциклопедический словарь

Система функций {φn(х)}, n = 1, 2, ..., заданных на отрезке [а, b] и удовлетворяющих следующему условию ортогональности: при k≠l, где ρ(х) некоторая функция, называемая весом. Например, тригонометрическая система 1, sin х, cos х, sin 2х,… … Энциклопедический словарь

Система ф ций {(фn(х)}, п=1, 2, ..., заданных на отрезке [а, b] и удовлетворяющих след, условию ортогональности при k не равно l, где р(х) нек рая ф ция, наз. весом. Напр., тригонометрич. система 1, sin х, cosх, sin 2х, cos 2x,... О.с.ф. с весом… … Естествознание. Энциклопедический словарь

Система функций {(φn (x)}, n = 1, 2,..., ортогональных с весом ρ (х) на отрезке [а, b], т. е. таких, что Примеры. Тригонометрическая система 1, cos nx, sin nx; n = 1, 2,..., О. с. ф. с весом 1 на отрезке [ π, π]. Бесселя … Большая советская энциклопедия

Ортогональными называются координаты в которых метрический тензор имеет диагональный вид. где d В ортогональных системах координат q = (q1, q², …, qd) координатные поверхности ортогональны друг другу. В частности, в декартовой системе координат… … Википедия

ортогональная многоканальная система - — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN ortogonal multiplex …

система координат (фотограмметрического) снимка - Правая ортогональная пространственная система координат, фиксируемая на фотограмметрическом снимке изображениями координатных меток. [ГОСТ Р 51833 2001] Тематики фотограмметрия … Справочник технического переводчика

система - 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации

Определение . Векторы a и b называются ортогональными (перпендикулярными) друг другу, если их скалярное произведение равно нулю, т.е. a × b = 0.

Для ненулевых векторов a и b равенство нулю скалярного произведения означает, что cosj = 0, т.е. . Нулевой вектор ортогонален любому вектору, т.к. a ×0 = 0.

Упражнение. Пусть и – ортогональные векторы. Тогда естественно считать диагональю прямоугольника со сторонами и . Докажите, что

,

т.е. квадрат длины диагонали прямоугольника равен сумме квадратов длин двух его непараллельных сторон (теорема Пифагора).

Определение. Система векторов a 1 ,…, a m называется ортогональной, если ортогональны любые два вектора этой системы .

Таким образом, для ортогональной системы векторов a 1 ,…,a m справедливо равенство:a i ×a j = 0 при i ¹ j , i = 1,…, m ; j = 1,…,m .

Теорема 1.5 . Ортогональная система, состоящая из ненулевых векторов, линейно независима. .

□ Доказательство проведем от противного. Предположим, что ортогональная система ненулевых векторов a 1 , …, a m линейно зависима. Тогда

l 1 a 1 + …+ l m a m = 0 , при этом . (1.15)

Пусть, например, l 1 ¹ 0. Домножим на a 1 обе части равенства (1.15):

l 1 a 1 ×a 1 + …+ l m a m ×a 1 = 0.

Все слагаемые, кроме первого, равны нулю в силу ортогональности системы a 1 , …, a m . Тогда l 1 a 1 ×a 1 =0, откуда следует a 1 = 0 , что противоречит условию. Наше предположение оказалось неверным. Значит, ортогональная система ненулевых векторов линейно независима. ■

Имеет место следующая теорема.

Теорема 1.6 . В пространстве R n всегда существует базис, состоящий из ортогональных векторов (ортогональный базис)
(без доказательства).

Ортогональные базисы удобны прежде всего тем, что коэффициенты разложения произвольного вектора по таким базисам определяются просто.

Пусть требуется найти разложение произвольного вектора b по ортогональному базису е 1 ,…,е n . Составим разложение этого вектора с неизвестными пока коэффициентами разложения по данному базису:

Умножим обе части этого равенства скалярно на вектор e 1 . В силу аксиом 2° и 3° скалярного произведения векторов получим

Так как векторы базиса е 1 ,…,е n взаимно ортогональны, то все скалярные произведения векторов базиса, за исключением первого, равны нулю, т.е. коэффициент определяется по формуле

.

Умножая поочередно равенство (1.16) на другие базисные векторы, мы получим простые формулы для вычисления коэффициентов разложения вектора b :

. (1.17)

Формулы (1.17) имеют смысл, поскольку .

Определение . Вектор a называется нормированным (или единичным), если его длина равна 1, т.е. (a , a )= 1.

Любой ненулевой вектор можно нормировать. Пусть a ¹ 0 . Тогда , и вектор есть нормированный вектор.

Определение . Система векторов е 1 ,…,е n называется ортонормированной, если она ортогональна и длина каждого вектора системы равна 1, т.е.

(1.18)

Так как в пространстве R n всегда существует ортогональный базис и векторы этого базиса можно нормировать, то в R n всегда существует ортонормированный базис.

Примером ортонормированного базиса пространства R n может служить система векторов е 1 ,=(1,0,…,0),…, е n =(0,0,…,1) со скалярным произведением, определенным равенством (1.9). В ортонормированном базисе е 1 ,=(1,0,…,0),…, е n =(0,0,…,1) формулы (1.17) для определения координат разложения вектора b имеют наиболее простой вид:

Пусть a и b – два произвольных вектора пространства R n с ортонормированным базисом е 1 ,=(1,0,…,0),…, е n =(0,0,…,1). Обозначим координаты векторов a и b в базисе е 1 ,…,е n соответственно через a 1 ,…,a n и b 1 ,…, b n и найдем выражение скалярного произведения этих векторов через их координаты в данном базисе, т.е. предположим, что

, .

Из последнего равенства в силу аксиом скалярного произведения и соотношений (1.18) получим

Окончательно имеем

. (1.19)

Таким образом, в ортонормированном базисе скалярное произведение двух любых векторов равно сумме произведений соответствующих координат этих векторов .

Рассмотрим теперь в n-мерном евклидовом пространстве R n совершенно произвольный (вообще говоря, не ортонормированный) базис и найдем выражение скалярного произведения двух произвольных векторов a и b через координаты этих векторов в указанном базисе.

система функций {(φ n (x )}, n = 1, 2,..., ортогональных с весом ρ (х ) на отрезке [а , b ], т. е. таких, что

Примеры. Тригонометрическая система 1, cos nx , sin nx ; n = 1, 2,..., - О. с. ф. с весом 1 на отрезке [-π, π]. Бесселя функции n = 1, 2,..., J ν (x ), образуют для каждого ν > - 1 / 2 О. с. ф. с весом х на отрезке .

Если каждая функция φ (х ) из О. с. ф. такова, что х) на число

Систематическое изучение О. с. ф. было начато в связи с методом Фурье решения краевых задач уравнений математической физики. Этот метод приводит, например, к разысканию решений Штурма - Лиувилля задачи (См. Штурма - Лиувилля задача) для уравнения [ρ(х ) у" ]" + q (x ) y = λу , удовлетворяющих граничным условиям у (а ) + hy" (a ) = 0, y (b ) + Hy" (b ) = 0, где h и Н - постоянные. Эти решения - т. н. собственные функции задачи - образуют О. с. ф. с весом ρ (х ) на отрезке [a , b ].

Чрезвычайно важный класс О. с. ф. - Ортогональные многочлены - был открыт П. Л. Чебышевым в его исследованиях по интерполированию способом наименьших квадратов и проблеме моментов. В 20 в. исследования по О. с. ф. проводятся в основном на базе теории интеграла и меры Лебега. Это способствовало выделению этих исследований в самостоятельный раздел математики. Одна из основных задач теории О. с. ф.- задача о разложении функции f (x ) в ряд вида п (х )} - О. с. ф. Если положить формально п (х )} - нормированная О. с. ф., и допустить возможность почленного интегрирования, то, умножая этот ряд на φ п (х ) ρ(х ) и интегрируя от а до b , получим:

Коэффициенты С п , называемые коэффициентами Фурье функции относительно системы {φ n (x )}, обладают следующим экстремальным свойством: линейная форма х):

имеет наименьшее значение по сравнению с ошибками, даваемыми при том же n другими линейными выражениями вида

Ряд ∑ ∞ n=1 C n φ n (x) с коэффициентами С п , вычисленными по формуле (*), называется рядом Фурье функции f (x ) по нормированной О. с. ф. {φ n (x )}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция f (x ) своими коэффициентами Фурье. О. с. ф., для которых это имеет место, называется полными, или замкнутыми. Условия замкнутости О. с. ф. могут быть даны в нескольких эквивалентных формах. 1) Любая непрерывная функция f (x ) может быть с любой степенью точности приближена в среднем линейными комбинациями функций φ k (x ), то есть C n φ n (x) сходится в среднем к функции f (x )]. 2) Для всякой функции f (x ), квадрат которой интегрируем относительно веса ρ(х ), выполняется условие замкнутости Ляпунова - Стеклова:

3) Не существует отличной от нуля функции с интегрируемым на отрезке [a , b ] квадратом, ортогональной ко всем функциям φ n (x ), n = 1, 2,....

Если рассматривать функции с интегрируемым квадратом как элементы гильбертова пространства (См. Гильбертово пространство), то нормированные О. с. ф. будут системами координатных ортов этого пространства, а разложение в ряд по нормированным О. с. ф. - разложением вектора по ортам. При этом подходе многие понятия теории нормированных О. с. ф. приобретают наглядный геометрический смысл. Например, формула (*) означает, что проекция вектора на орт равна скалярному произведению вектора и орта; равенство Ляпунова - Стеклова может быть истолковано как теорема Пифагора для бесконечномерного пространства: квадрат длины вектора равен сумме квадратов его проекций на оси координат; замкнутость О. с. ф. означает, что наименьшее замкнутое подпространство, содержащее все векторы этой системы, совпадает со всем пространством и т.д.

Лит.: Толстов Г. П., Ряды Фурье, 2 изд., М., 1960; Натансон И. П., Конструктивная теория функций, М. - Л., 1949; его же, Теория функций вещественной переменной, 2 изд., М., 1957; Джексон Д., Ряды Фурье и ортогональные полиномы, пер. с англ., М., 1948; Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958.

• - группа всех линейных преобразований n-мерного векторного пространства Vнад полем k, сохраняющих фиксированную невырожденную квадратичную форму Q на V)=Q для любого)...

  Математическая энциклопедия

• - матрица над коммутативным кольцом R с единицей 1, для к-рой транспонированная матрица совпадает с обратной. Определитель О. м. равен +1...

  Математическая энциклопедия

• - сеть, у к-рой касательные в нек-рой точке к линиям различных семейств ортогональны. Примеры О. с.: асимптотическая сеть на минимальной поверхности, кривизны линий сеть. А. В. Иванов...

  Математическая энциклопедия

• - 1) О....

  Математическая энциклопедия

• - ортогональный массив, ОА - матрица размера kx N, элементы к-рой суть числа 1, 2, .....

  Математическая энциклопедия

• - см. Изогональная траектория...

  Математическая энциклопедия

• - ортонормированная система функций {j}нек-рого гильбертова пространства Нтакая, что в H не существует функции, ортогональной всем функциям данного семейства...

  Математическая энциклопедия

• - см. Проекция...

  Большой энциклопедический политехнический словарь

• - определение взаиимоподчиненности функций различных объектов...

  Словарь бизнес терминов

• - усиление функций, один из гл. путей прогрессивного преобразования органов в ходе эволюции животных. И. ф. обычно связана с усложнением строения органов и организма в целом...

  Биологический энциклопедический словарь

• - усиление функций, один из главных путей прогрессивного преобразования органов в ходе эволюции животных. И. ф. связана с усложнением строения органов и приводит к общему подъёму уровня жизнедеятельности...
• - порядка n Матрица...

  Большая Советская энциклопедия

• - частный случай параллельной проекции, когда ось или плоскость проекций перпендикулярна направлению проектирования...

  Большая Советская энциклопедия

• - система функций {}, n = 1, 2,..., ортогональных с весом ρ на отрезке, т. е. таких, что Примеры. Тригонометрическая система 1, cos nx, sin nx; n = 1, 2,..., - О. с. ф. с весом 1 на отрезке...

  Большая Советская энциклопедия

• - такая система функций Ф = {φ}, определённых на отрезке, что не существует функции f , для которой,...

  Большая Советская энциклопедия

• - ОРТОГОНАЛЬНАЯ система ФУНКЦИЙ - система функций??n?, n=1, 2,.....

  Большой энциклопедический словарь

"Ортогональная система функций" в книгах

Параграф XXIV Старая система позиционных войн и современная система маршей