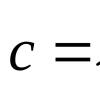Обобщённая фу́нкция или распределе́ние - математическое понятие, обобщающее классическое понятие функции . Потребность в таком обобщении возникает во многих физических и математических задачах.

Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя , (пространственную) плотность простого или двойного слоя , интенсивность мгновенного источника и т. д.

С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки. Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин. Математика начала ХХ века не имела нужных строгих формализмов для оперирования с новым классом зависимостей величин, открытых в физике.

Важный вклад в формирование нового математического подхода к понятию функции в физике принадлежит Η. Μ. Гюнтеру , который предлагал рассматривать вместо точечных характеристик типа плотности соответствующие функции множеств еще в 1916 году и пытался переосмылить на этой основе понятие решения уравнения математической физики. Однако Н.М. Гюнтер не связывал эти идеи с нарождающимся функциональным анализом и квантовой механикой. Фундаментальные идеи, основанные на использовании пространств финитных функций и принципиально новом понятии обобщенной производной были сформулированы в 1935 году С. Л. Соболевым . К аналогичным идеям самостоятельно через десять лет пришел выдающийся французский математик Л. Шварц , привлекший разработанную к тому времени теорию локально выпуклых пространств и построивший преобразование Фурье обобщенных функций . Соболев и Шварц являются создателями теории распределений - обобщенных функций. Обобщённые функции эмпирически использовались Дираком в его исследованиях по квантовой механике .

В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений .

Энциклопедичный YouTube

• 1 / 5

  Формально обобщённая функция f {\displaystyle f} определяется как линейный непрерывный функционал (f , φ) {\displaystyle \left(f,\varphi \right)} над тем или иным векторным пространством достаточно «хороших функций» (так называемых основных функций ): f: φ ↦ (f , φ) {\displaystyle f:\varphi \mapsto (f,\;\varphi)} .

  Условие линейности: (f , α 1 φ 1 + α 2 φ 2) = α 1 (f , φ 1) + α 2 (f , φ 2) {\displaystyle \left(f,\alpha _{1}\varphi _{1}+\alpha _{2}\varphi _{2}\right)=\alpha _{1}\left(f,\varphi _{1}\right)+\alpha _{2}\left(f,\varphi _{2}\right)} .

  Условие непрерывности: если φ ν → 0 {\displaystyle \varphi _{\nu }\rightarrow 0} , то (f , φ ν) → 0 {\displaystyle \left(f,\varphi _{\nu }\right)\rightarrow 0} .

  Важным примером основного пространства является пространство - совокупность финитных -функций на , снабжённая естественной для неё топологией: последовательность функций из D (R n) {\displaystyle D(\mathbb {R} ^{n})} сходится, если их носители принадлежат фиксированному шару и в нём они C ∞ {\displaystyle C^{\infty }} -сходятся.

  Действительно, в противном случае получилось бы противоречие:

  (x δ) ρ = 0 ⋅ ρ = 0 , {\displaystyle (x\delta)\rho =0\cdot \rho =0,} (x ρ) δ = 1 ⋅ δ = δ . {\displaystyle (x\rho)\delta =1\cdot \delta =\delta .}

  Впрочем, возможно определить умножение любых обобщённых функций, если снять достаточно жёсткое требование, чтобы сужение этой операции на множество непрерывных функций совпадало с обычным произведением. В частности, Ю. М. Широков построил некоммутативную алгебру обобщённых функций . Нынче в Западной Европе и Америке очень популярной (см., напр., список цитированных работ в ) является теория обобщённых функций Коломбо (одним из первоисточников которой является книга , для первоначального ознакомления с гораздо чаще используемой на практике т.н. "специальной" алгеброй Коломбо можно просмотреть параграф 8.5 из ). В рамках этой теории обобщённые функции являются классами эквивалентности некоторой фактор-алгебры. Преимуществом алгебры Коломбо является то, что она как ассоциативна, так и коммутативна. Умножение обобщённых функций Коломбо совпадает с обычным умножением при сужении на множество всех гладких (т.е., бесконечно непрерывно дифференцируемых) функций, несостыковка же с умножением непрерывных (но не гладких) функций разрешается при помощи введения понятия ассоциации (менее строгого, чем понятие эквивалентности). Также рассматриваемое умножение прекрасно согласуется со стандартными операциями классического анализа (напр., дифференцированием).

  Дифференцирование

  Пусть f ∈ D ′ (R n) {\displaystyle f\in D"(\mathbb {R} ^{n})} . Обобщённая (слабая) производная обобщённой функции ∂ f ∂ x i {\displaystyle {\frac {\partial f}{\partial x_{i}}}} определяется равенством

  (∂ f ∂ x i , φ) = − (f , ∂ φ ∂ x i) . {\displaystyle \left({\frac {\partial f}{\partial x_{i}}},\;\varphi \right)=-\left(f,\;{\frac {\partial \varphi }{\partial x_{i}}}\right).}

  Так как операция φ ↦ ∂ φ ∂ x i {\displaystyle \varphi \mapsto {\frac {\partial \varphi }{\partial x_{i}}}} линейна и непрерывна из D (R n) {\displaystyle D(\mathbb {R} ^{n})} в D (R n) {\displaystyle D(\mathbb {R} ^{n})} , то функционал, определяемый правой частью равенства, есть обобщённая функция.

  из есть слабый предел функций из D (R n) {\displaystyle D(\mathbb {R} ^{n})} . Это свойство иногда берётся в качестве исходного для определения обобщённой функции, из полноты пространства обобщённых функций это приводит к эквивалентному определению.
• Любая обобщённая функция из D ′ (R n) {\displaystyle D"(\mathbb {R} ^{n})} бесконечно дифференцируема (в обобщённом смысле).
• Дифференцирование не увеличивает носителя обобщённой функции.
• Для обобщённых функций справедлива формула Лейбница для дифференцирования произведения a f {\displaystyle af} , где a ∈ C ∞ (R n) {\displaystyle a\in C^{\infty }(\mathbb {R} ^{n})} .
• Всякая обобщённая функция f {\displaystyle f} из S ′ (R n) {\displaystyle S"(\mathbb {R} ^{n})} или E ′ (R n) {\displaystyle E"(\mathbb {R} ^{n})} есть некоторая частная производная от непрерывной функции в R n {\displaystyle \mathbb {R} ^{n}} .
• Для любой обобщённой функции f {\displaystyle f} порядка N {\displaystyle N} с носителем в точке 0 существует единственное представление (f , φ) {\displaystyle (f,\;\varphi)} в виде линейной комбинации частных производных φ {\displaystyle \varphi } в нуле, с порядком меньшим либо равным N {\displaystyle N} .

8. Обобщенные функции

8.1. Понятие обобщенной функции

Понятие обобщенной функции позволяет выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, плотность точечного заряда.

Попытаемся определить плотность, создаваемую материальной точкой массы, равной единице. Чтобы определить эту плотность, распределим (или, как говорят, “размажем”) единичную массу равномерно внутри окрестности радиуса с центром в нуле. В результате получим среднюю плотность , равную

Но нас интересует плотность при . Обозначим ее через . Причем сначала в качестве искомой плотности возьмем поточечный предел последовательности средних плотностей при , то есть функцию

и интеграл от этой функции по всей оси давал бы полную массу вещества, то есть

Но с математической точки зрения, такое невозможно, так как для функции , определенной нашим способом:

Это значит, что данная функция не восстанавливает массу и поэтому не может быть принята в качестве искомой плотности. Итак, поточечный предел последовательности средних плотностей не подходит для наших целей. Поэтому требуются корректные определения для этого случая.

Выход состоит в том, чтобы искать другой, так называемый, слабый предел последовательности . А именно, будем рассматривать не предел в каждой точке x , а предел следующих интегралов где -произвольная непрерывная функция. Ясно, что


Эта формула обозначает, что слабым пределом последовательности функций при является оператор, точнее функционал , сопоставляющий каждой непрерывной функции число -ее значение в точке . Вот этот функционал мы и примем в качестве искомой плотности , это и есть известная Дирака.

Можно ли представить -функцию в виде: с какой-либо локально интегрируемой функцией?

Для этого нужно, чтобы при . Но такой функции нет.

Определение . Задать вещественный функционал f на множестве функций M значит указать правило, по которому каждой функции сопоставляется вещественное число. Мы будем рассматривать в качестве множества M совокупность вещественных функций , которые определены при , непрерывны и имеют производные любого порядка. Кроме того, будем предполагать, что функции финитны , то есть в случае конечного интервала (a,b ) существуют такие окрестности точек a и b (свои для каждой из функций ), где эти функции обращаются в нуль. В случае бесконечного интервала (a,b ), кроме того, существует такая постоянная A, причем для каждой из функций -своя, что вне интервала (-A,A ) функция обращается в нуль. Такие функции будем называть основными, а всю их совокупность D (a,b )-основным пространством .

Пример, такой функции представлен на рисунке 2.

Проверим, что данная функция является основной. Для этого достаточно показать, что она бесконечно-дифференцируема. Во всех точках кроме это свойство очевидно. Проверим его выполнение в точке .

Пусть , тогда по правилу Лопиталя

то есть функция дифференцируема.

Аналогично проверяется непрерывность производной любого порядка. В этом легко убедиться, заметив, что для любого непрерывного n .

Чтобы определить пространство основных функций D (a,b ), нужно задать действия с ними. Точнее, надо проверить, что линейные операции не выводят из множества основных функций.

1. , причем сумма конечна, то есть .

Если -основная функция, то -основная функция.

2. , где - конечное число.

Если - основная функция, то -основная функция.

Линейный оператор, который каждому элементу пространства ставит в соответствие число, называется линейным функционалом (вещественным или комплексным).

Будем обозначать действие функционала f на основную функцию следующим образом :
.

Обобщенная функция (распределение) –это линейный непрерывный функционал на пространстве основных функций, то есть функционал f , удовлетворяющий условиям :

1., где (линейность);

2. Если в D , то (непрерывность). f

Сделаем замену, пусть , тогда

Материал из Википедии - свободной энциклопедии

Обобщённая фу́нкция или распределе́ние - математическое понятие, обобщающее классическое понятие функции . Потребность в таком обобщении возникает во многих физических и математических задачах.

Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя , (пространственную) плотность простого или двойного слоя , интенсивность мгновенного источника и т. д.

С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки. Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин. Математика начала ХХ века не имела нужных строгих формализмов для оперирования с новым классом зависимостей величин, открытых в физике.

Важный вклад в формирование нового математического подхода к понятию функции в физике принадлежит Η. Μ. Гюнтеру , который предлагал рассматривать вместо точечных характеристик типа плотности соответствующие функции множеств еще в 1916 году и пытался переосмылить на этой основе понятие решения уравнения математической физики. Однако Н.М. Гюнтер не связывал эти идеи с нарождающимся функциональным анализом и квантовой механикой. Фундаментальные идеи, основанные на использовании пространств финитных функций и принципиально новом понятии обобщенной производной были сформулированы в 1935 году С. Л. Соболевым . К аналогичным идеям самостоятельно через десять лет пришел выдающийся французский математик Л. Шварц , привлекший разработанную к тому времени теорию локально выпуклых пространств и построивший преобразование Фурье обобщенных функций . Соболев и Шварц являются создателями теории распределений - обобщенных функций. Обобщённые функции эмпирически использовались Дираком в его исследованиях по квантовой механике .

В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений .

Определение

Формально обобщённая функция $f$ определяется как линейный непрерывный функционал $\backslash left\; (f,\; \backslash varphi\; \backslash right)$ над тем или иным векторным пространством достаточно «хороших функций» $\backslash varphi$ (так называемых основных функций ): $f:\backslash varphi\backslash mapsto(f,\backslash ;\backslash varphi)$ .

Условие линейности: $\backslash left\; (f,\; \backslash alpha\_\{1\}\; \backslash varphi\_\{1\}\; +\; \backslash alpha\_\{2\}\; \backslash varphi\_\{2\}\backslash right)\; =\; \backslash alpha\_\{1\}\; \backslash left\; (f,\; \backslash varphi\_\{1\}\; \backslash right)\; +\; \backslash alpha\_\{2\}\; \backslash left\; (f,\; \backslash varphi\_\{2\}\; \backslash right)$.

Условие непрерывности: если $\backslash varphi\_\{\backslash nu\}\; \backslash rightarrow\; 0$, то $\backslash left\; (f,\; \backslash varphi\_\{\backslash nu\}\; \backslash right)\; \backslash rightarrow\; 0$.

Важным примером основного пространства является пространство $D(\backslash R^n)$ - совокупность финитных $C^\backslash infty$-функций на $\backslash R^n$, снабжённая естественной для неё топологией: последовательность функций из $D(\backslash R^n)$ сходится, если их носители принадлежат фиксированному шару и в нём они $C^\backslash infty$-сходятся.

Действительно, в противном случае получилось бы противоречие:

$(x\backslash delta)\backslash rho=0\backslash cdot\backslash rho=0,$ $(x\backslash rho)\backslash delta=1\backslash cdot\backslash delta=\backslash delta.$

Впрочем, возможно определить умножение любых обобщённых функций, если снять достаточно жёсткое требование, чтобы сужение этой операции на множество непрерывных функций совпадало с обычным произведением. В частности, Ю. М. Широков построил некоммутативную алгебру обобщённых функций . Нынче в Западной Европе и Америке очень популярной (см., напр., список цитированных работ в ) является теория (одним из первоисточников которой является книга , для первоначального ознакомления с гораздо чаще используемой на практике т.н. "специальной" алгеброй Коломбо можно просмотреть параграф 8.5 из ). В рамках этой теории обобщённые функции являются классами эквивалентности некоторой фактор-алгебры. Преимуществом алгебры Коломбо является то, что она как ассоциативна, так и коммутативна. Умножение обобщённых функций Коломбо совпадает с обычным умножением при сужении на множество всех гладких (т.е., бесконечно непрерывно дифференцируемых) функций, несостыковка же с умножением непрерывных (но не гладких) функций разрешается при помощи введения понятия ассоциации (менее строгого, чем понятие эквивалентности). Также рассматриваемое умножение прекрасно согласуется со стандартными операциями классического анализа (напр., дифференцированием).

Дифференцирование

Пусть $f\backslash in\; D"(\backslash R^n)$. Обобщённая (слабая) производная обобщённой функции $\backslash frac\{\backslash partial\; f\}\{\backslash partial\; x\_i\}$ определяется равенством

$\backslash left(\backslash frac\{\backslash partial\; f\}\{\backslash partial\; x\_i\},\backslash ;\backslash varphi\backslash right)=-\backslash left(f,\backslash ;\backslash frac\{\backslash partial\backslash varphi\}\{\backslash partial\; x\_i\}\backslash right).$

Так как операция $\backslash varphi\backslash mapsto\backslash frac\{\backslash partial\backslash varphi\}\{\backslash partial\; x\_i\}$ линейна и непрерывна из $D(\backslash R^n)$ в $D(\backslash R^n)$, то функционал, определяемый правой частью равенства, есть обобщённая функция.

Свойства

• Пространство $D"(\backslash R^n)$ - полное : если последовательность обобщённых функций $f\_i$ из $D"(\backslash R^n)$ такова, что для любой функции $\backslash varphi\backslash in\; D(\backslash R^n)$ числовая последовательность $(f\_i,\backslash ;\backslash varphi)$ сходится, то функционал
$(f,\backslash ;\backslash varphi)=\; \backslash lim\_\{i\backslash to\backslash infty\}(f\_i,\backslash ;\backslash varphi)$ принадлежит $D"(\backslash R^n)$.
• Всякая $f$ из $D"(\backslash R^n)$ есть слабый предел функций из $D(\backslash R^n)$. Это свойство иногда берётся в качестве исходного для определения обобщённой функции, из полноты пространства обобщённых функций это приводит к эквивалентному определению.
• Любая обобщённая функция из $D"(\backslash R^n)$ бесконечно дифференцируема (в обобщённом смысле).
• Дифференцирование не увеличивает носителя обобщённой функции.
• Для обобщённых функций справедлива формула Лейбница для дифференцирования произведения $af$, где $a\backslash in\; C^\backslash infty(\backslash R^n)$.
• Всякая обобщённая функция $f$ из $S"(\backslash R^n)$ или $E"(\backslash R^n)$ есть некоторая частная производная от непрерывной функции в $\backslash R^n$.
• Для любой обобщённой функции $f$ порядка $N$ с носителем в точке 0 существует единственное представление $(f,\backslash ;\backslash varphi)$ в виде линейной комбинации частных производных $\backslash varphi$ в нуле, с порядком меньшим либо равным $N$.

Примеры

Дельта-функция получается при вычислении интеграла Фурье от константы:

$\backslash int\backslash limits\_\{-\backslash infty\}^\{\backslash infty\}e^\{ipx\}\backslash ,dp=2\backslash pi\backslash delta(x).$

Напишите отзыв о статье "Обобщённая функция"

Примечания

См. также

Отрывок, характеризующий Обобщённая функция

– Вот глупости! Очень мне нужно, – сказал Ростов, бросая письмо под стол.
– Зачем ты это бросил? – спросил Борис.
– Письмо какое то рекомендательное, чорта ли мне в письме!
– Как чорта ли в письме? – поднимая и читая надпись, сказал Борис. – Письмо это очень нужное для тебя.
– Мне ничего не нужно, и я в адъютанты ни к кому не пойду.
– Отчего же? – спросил Борис.
– Лакейская должность!
– Ты всё такой же мечтатель, я вижу, – покачивая головой, сказал Борис.
– А ты всё такой же дипломат. Ну, да не в том дело… Ну, ты что? – спросил Ростов.
– Да вот, как видишь. До сих пор всё хорошо; но признаюсь, желал бы я очень попасть в адъютанты, а не оставаться во фронте.
– Зачем?
– Затем, что, уже раз пойдя по карьере военной службы, надо стараться делать, коль возможно, блестящую карьеру.
– Да, вот как! – сказал Ростов, видимо думая о другом.
Он пристально и вопросительно смотрел в глаза своему другу, видимо тщетно отыскивая разрешение какого то вопроса.
Старик Гаврило принес вино.
– Не послать ли теперь за Альфонс Карлычем? – сказал Борис. – Он выпьет с тобою, а я не могу.
– Пошли, пошли! Ну, что эта немчура? – сказал Ростов с презрительной улыбкой.
– Он очень, очень хороший, честный и приятный человек, – сказал Борис.
Ростов пристально еще раз посмотрел в глаза Борису и вздохнул. Берг вернулся, и за бутылкой вина разговор между тремя офицерами оживился. Гвардейцы рассказывали Ростову о своем походе, о том, как их чествовали в России, Польше и за границей. Рассказывали о словах и поступках их командира, великого князя, анекдоты о его доброте и вспыльчивости. Берг, как и обыкновенно, молчал, когда дело касалось не лично его, но по случаю анекдотов о вспыльчивости великого князя с наслаждением рассказал, как в Галиции ему удалось говорить с великим князем, когда он объезжал полки и гневался за неправильность движения. С приятной улыбкой на лице он рассказал, как великий князь, очень разгневанный, подъехав к нему, закричал: «Арнауты!» (Арнауты – была любимая поговорка цесаревича, когда он был в гневе) и потребовал ротного командира.
– Поверите ли, граф, я ничего не испугался, потому что я знал, что я прав. Я, знаете, граф, не хвалясь, могу сказать, что я приказы по полку наизусть знаю и устав тоже знаю, как Отче наш на небесех. Поэтому, граф, у меня по роте упущений не бывает. Вот моя совесть и спокойна. Я явился. (Берг привстал и представил в лицах, как он с рукой к козырьку явился. Действительно, трудно было изобразить в лице более почтительности и самодовольства.) Уж он меня пушил, как это говорится, пушил, пушил; пушил не на живот, а на смерть, как говорится; и «Арнауты», и черти, и в Сибирь, – говорил Берг, проницательно улыбаясь. – Я знаю, что я прав, и потому молчу: не так ли, граф? «Что, ты немой, что ли?» он закричал. Я всё молчу. Что ж вы думаете, граф? На другой день и в приказе не было: вот что значит не потеряться. Так то, граф, – говорил Берг, закуривая трубку и пуская колечки.
– Да, это славно, – улыбаясь, сказал Ростов.
Но Борис, заметив, что Ростов сбирался посмеяться над Бергом, искусно отклонил разговор. Он попросил Ростова рассказать о том, как и где он получил рану. Ростову это было приятно, и он начал рассказывать, во время рассказа всё более и более одушевляясь. Он рассказал им свое Шенграбенское дело совершенно так, как обыкновенно рассказывают про сражения участвовавшие в них, то есть так, как им хотелось бы, чтобы оно было, так, как они слыхали от других рассказчиков, так, как красивее было рассказывать, но совершенно не так, как оно было. Ростов был правдивый молодой человек, он ни за что умышленно не сказал бы неправды. Он начал рассказывать с намерением рассказать всё, как оно точно было, но незаметно, невольно и неизбежно для себя перешел в неправду. Ежели бы он рассказал правду этим слушателям, которые, как и он сам, слышали уже множество раз рассказы об атаках и составили себе определенное понятие о том, что такое была атака, и ожидали точно такого же рассказа, – или бы они не поверили ему, или, что еще хуже, подумали бы, что Ростов был сам виноват в том, что с ним не случилось того, что случается обыкновенно с рассказчиками кавалерийских атак. Не мог он им рассказать так просто, что поехали все рысью, он упал с лошади, свихнул руку и изо всех сил побежал в лес от француза. Кроме того, для того чтобы рассказать всё, как было, надо было сделать усилие над собой, чтобы рассказать только то, что было. Рассказать правду очень трудно; и молодые люди редко на это способны. Они ждали рассказа о том, как горел он весь в огне, сам себя не помня, как буря, налетал на каре; как врубался в него, рубил направо и налево; как сабля отведала мяса, и как он падал в изнеможении, и тому подобное. И он рассказал им всё это.
В середине его рассказа, в то время как он говорил: «ты не можешь представить, какое странное чувство бешенства испытываешь во время атаки», в комнату вошел князь Андрей Болконский, которого ждал Борис. Князь Андрей, любивший покровительственные отношения к молодым людям, польщенный тем, что к нему обращались за протекцией, и хорошо расположенный к Борису, который умел ему понравиться накануне, желал исполнить желание молодого человека. Присланный с бумагами от Кутузова к цесаревичу, он зашел к молодому человеку, надеясь застать его одного. Войдя в комнату и увидав рассказывающего военные похождения армейского гусара (сорт людей, которых терпеть не мог князь Андрей), он ласково улыбнулся Борису, поморщился, прищурился на Ростова и, слегка поклонившись, устало и лениво сел на диван. Ему неприятно было, что он попал в дурное общество. Ростов вспыхнул, поняв это. Но это было ему всё равно: это был чужой человек. Но, взглянув на Бориса, он увидал, что и ему как будто стыдно за армейского гусара. Несмотря на неприятный насмешливый тон князя Андрея, несмотря на общее презрение, которое с своей армейской боевой точки зрения имел Ростов ко всем этим штабным адъютантикам, к которым, очевидно, причислялся и вошедший, Ростов почувствовал себя сконфуженным, покраснел и замолчал. Борис спросил, какие новости в штабе, и что, без нескромности, слышно о наших предположениях?
– Вероятно, пойдут вперед, – видимо, не желая при посторонних говорить более, отвечал Болконский.
Берг воспользовался случаем спросить с особенною учтивостию, будут ли выдавать теперь, как слышно было, удвоенное фуражное армейским ротным командирам? На это князь Андрей с улыбкой отвечал, что он не может судить о столь важных государственных распоряжениях, и Берг радостно рассмеялся.
– Об вашем деле, – обратился князь Андрей опять к Борису, – мы поговорим после, и он оглянулся на Ростова. – Вы приходите ко мне после смотра, мы всё сделаем, что можно будет.
И, оглянув комнату, он обратился к Ростову, которого положение детского непреодолимого конфуза, переходящего в озлобление, он и не удостоивал заметить, и сказал:
– Вы, кажется, про Шенграбенское дело рассказывали? Вы были там?
– Я был там, – с озлоблением сказал Ростов, как будто бы этим желая оскорбить адъютанта.
Болконский заметил состояние гусара, и оно ему показалось забавно. Он слегка презрительно улыбнулся.
– Да! много теперь рассказов про это дело!
– Да, рассказов, – громко заговорил Ростов, вдруг сделавшимися бешеными глазами глядя то на Бориса, то на Болконского, – да, рассказов много, но наши рассказы – рассказы тех, которые были в самом огне неприятеля, наши рассказы имеют вес, а не рассказы тех штабных молодчиков, которые получают награды, ничего не делая.
– К которым, вы предполагаете, что я принадлежу? – спокойно и особенно приятно улыбаясь, проговорил князь Андрей.
Странное чувство озлобления и вместе с тем уважения к спокойствию этой фигуры соединялось в это время в душе Ростова.
– Я говорю не про вас, – сказал он, – я вас не знаю и, признаюсь, не желаю знать. Я говорю вообще про штабных.
– А я вам вот что скажу, – с спокойною властию в голосе перебил его князь Андрей. – Вы хотите оскорбить меня, и я готов согласиться с вами, что это очень легко сделать, ежели вы не будете иметь достаточного уважения к самому себе; но согласитесь, что и время и место весьма дурно для этого выбраны. На днях всем нам придется быть на большой, более серьезной дуэли, а кроме того, Друбецкой, который говорит, что он ваш старый приятель, нисколько не виноват в том, что моя физиономия имела несчастие вам не понравиться. Впрочем, – сказал он, вставая, – вы знаете мою фамилию и знаете, где найти меня; но не забудьте, – прибавил он, – что я не считаю нисколько ни себя, ни вас оскорбленным, и мой совет, как человека старше вас, оставить это дело без последствий. Так в пятницу, после смотра, я жду вас, Друбецкой; до свидания, – заключил князь Андрей и вышел, поклонившись обоим.
Ростов вспомнил то, что ему надо было ответить, только тогда, когда он уже вышел. И еще более был он сердит за то, что забыл сказать это. Ростов сейчас же велел подать свою лошадь и, сухо простившись с Борисом, поехал к себе. Ехать ли ему завтра в главную квартиру и вызвать этого ломающегося адъютанта или, в самом деле, оставить это дело так? был вопрос, который мучил его всю дорогу. То он с злобой думал о том, с каким бы удовольствием он увидал испуг этого маленького, слабого и гордого человечка под его пистолетом, то он с удивлением чувствовал, что из всех людей, которых он знал, никого бы он столько не желал иметь своим другом, как этого ненавидимого им адъютантика.

На другой день свидания Бориса с Ростовым был смотр австрийских и русских войск, как свежих, пришедших из России, так и тех, которые вернулись из похода с Кутузовым. Оба императора, русский с наследником цесаревичем и австрийский с эрцгерцогом, делали этот смотр союзной 80 титысячной армии.
С раннего утра начали двигаться щегольски вычищенные и убранные войска, выстраиваясь на поле перед крепостью. То двигались тысячи ног и штыков с развевавшимися знаменами и по команде офицеров останавливались, заворачивались и строились в интервалах, обходя другие такие же массы пехоты в других мундирах; то мерным топотом и бряцанием звучала нарядная кавалерия в синих, красных, зеленых шитых мундирах с расшитыми музыкантами впереди, на вороных, рыжих, серых лошадях; то, растягиваясь с своим медным звуком подрагивающих на лафетах, вычищенных, блестящих пушек и с своим запахом пальников, ползла между пехотой и кавалерией артиллерия и расставлялась на назначенных местах. Не только генералы в полной парадной форме, с перетянутыми донельзя толстыми и тонкими талиями и красневшими, подпертыми воротниками, шеями, в шарфах и всех орденах; не только припомаженные, расфранченные офицеры, но каждый солдат, – с свежим, вымытым и выбритым лицом и до последней возможности блеска вычищенной аммуницией, каждая лошадь, выхоленная так, что, как атлас, светилась на ней шерсть и волосок к волоску лежала примоченная гривка, – все чувствовали, что совершается что то нешуточное, значительное и торжественное. Каждый генерал и солдат чувствовали свое ничтожество, сознавая себя песчинкой в этом море людей, и вместе чувствовали свое могущество, сознавая себя частью этого огромного целого.
С раннего утра начались напряженные хлопоты и усилия, и в 10 часов всё пришло в требуемый порядок. На огромном поле стали ряды. Армия вся была вытянута в три линии. Спереди кавалерия, сзади артиллерия, еще сзади пехота.
Между каждым рядом войск была как бы улица. Резко отделялись одна от другой три части этой армии: боевая Кутузовская (в которой на правом фланге в передней линии стояли павлоградцы), пришедшие из России армейские и гвардейские полки и австрийское войско. Но все стояли под одну линию, под одним начальством и в одинаковом порядке.
Как ветер по листьям пронесся взволнованный шопот: «едут! едут!» Послышались испуганные голоса, и по всем войскам пробежала волна суеты последних приготовлений.

Обобщенные функции математическое понятие, обобщающее классическое понятие функции. Обобщенные функции были введены впервые в конце 20-х гг. XX в. П. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие дельта-функции и ее производных. Основы математической теории обобщенных функций были заложены С.Л. Соболевым в 1936 году при решении задачи Коши для гиперболических уравнений, а в послевоенные годы французский математик Л. Шварц дал систематическое изложение теории обобщенных функций. Важную роль в формировании теории обобщенных функций сыграли работы Ж. Адамара, в которых в связи с изучением фундаментальных решений волновых уравнений рассмотрены сходящиеся интегралы, а также работы М. Рисса.

С другой стороны, к теории обобщенных функций вплотную подводит теория С. Бохнера преобразований Фурье функций степенного роста. Эти преобразования Фурье являются по существу обобщенными функциями и выступают у С. Бохнера как формальные производные непрерывных функций. Обобщенные функции необыкновенно быстро, буквально за два-три года, приобрели чрезвычайно широкую популярность. Достаточно указать хотя бы на тот факт, что количество математических работ, в которых встречается дельта-функция, возросло во много раз.

В дальнейшем теорию обобщенных функций интенсивно развивали многие математики, главным образом из-за потребностей математической физики. Теория обобщенных функций имеет многочисленные применения и все шире входит в обиход физика, математика и инженера.

Формально обобщенные функции определяются как линейные непрерывные функционалы над тем или иным линейным пространством основных функций. Основным пространством функций является, например, совокупность бесконечно дифференцируемых финитных функций, снабженная надлежащей сходимостью (или точнее топологией). При этом обычные локально суммируемые функции отождествляются с функционалами (регулярными обобщенными функциями) вида:

Произвольная обобщенная функция определяется как функционал, задаваемый равенством:

Следовательно, каждая обобщенная функция бесконечно дифференцируема. Равенство (2) в силу (1) есть не что иное, как обобщение формулы интегрирования по частям для дифференцируемых в обычном смысле функций, так что в этом случае оба понятия производной совпадают.

Сходимость на (линейном) множестве обобщенных функций вводится как слабая сходимость функционалов. Оказывается, что операция дифференцирования обобщенных функций непрерывна, а сходящаяся последовательность обобщенных функций разрешает почленное дифференцирование бесконечное число раз.

Вводятся и другие операции над обобщенными функциями, например свертка, преобразование Фурье и Лапласа. Теория этих операций приобретает наиболее простую и законченную форму в рамках понятия обобщенных функций, расширяющих возможности классического математического анализа. Поэтому использование обобщенные функции существенно расширяет круг рассматриваемых задач и приводит к значительным упрощениям, автоматизируя элементарные операции.

Функция Дирака: , описывает плотность массы (заряда), сосредоточенной в точке, единичный импульс;

Функция Хевисайда: , при, при, ; производная от этой функции равна единичному импульсу;

Плотность диполя момента в точке, ориентированного вдоль оси;

Плотность простого слоя на поверхности с поверхностной плотностью;

Плотность двойного слоя на поверхности с поверхностной плотностью момента диполей, ориентированных вдоль направления нормали;

Свертка ньютонов, потенциал с плотностью, где - любая обобщенная функция (например, из первых пяти пунктов);

Общее решение уравнения колебаний струны задается формулой, где и любые обобщенные функции.