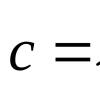Виды матриц. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому и треугольному виду. Многочленные матрицы

Любая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду , определенному формулой

где форма f ранга от n неизвестных; числа, , считаются положительными, но часть слагаемых формулы (VII.5) могут быть отрицательными.

При таком условии заменой , ; и , невырожденное линейное преобразование приводит квадратичную форму к нормальному виду, то есть

Общее число квадратов равно рангу квадратичной формы.

Существует много линейных преобразований, приводящих квадратичную форму к нормальному виду (VII.6), но с точностью до расположения знаков такое приведение единственное .

Для квадратичных действительных форм выполняется закон инерции . Число положительных и отрицательных квадратов в нормальном виде, к которому приводится данная квадратичная форма с действительными коэффициентами действительным линейным преобразованием, не зависит от выбора этого преобразования.

Число положительных (отрицательных) квадратов в нормальной форме формы f называется положительным (отрицательным) индексом инерции (в формуле (VII.6) это k ), разница между положительными и отрицательными индексами инерции называется сигнатурой формы f (в формуле (VII.6) она равна r -k ).

Пусть дана квадратная матрица размерности n квадратичной формы f . Миноры, расположенные по главной диагонали этой матрицы, порядков 1, 2, …, n , последний из них совпадает с определителем матрицы , , то есть

называются главными минорами формы f .

Теорема VII.1. Квадратичная форма f от n неизвестных с действительными коэффициентами тогда и только тогда будет состоять из положительных членов, когда все главные миноры положительны.

Пример VII.3. Квадратичная форма

положительно определена, так как все главные миноры матрицы положительны:

, , .

Приводить квадратичную форму к каноническому виду можно, как уже отмечалось, многими способами, но нормальный вид один. Покажем это на примере.

Пример VII.4. Привести к каноническому виду квадратичную форму .

Решение . Зададим линейное преобразование:

1) тогда получим .

Для другого преобразования имеем

2) тогда получим .

Нормальный вид квадратичной формы, которому соответствуют оба канонических вида, .

Упражнение. Проверить справедливость полученных формул непосредственной подстановкой преобразований 1) и 2) в исходную квадратичную форму.

Вполне естественно возникает вопрос: «Как найти матрицу линейного преобразования (оператора)?»

Прежде чем перейти к рассмотрению следующего примера, дадим некоторые пояснения. Не нарушая сущности общего подхода, ограничимся уравнением

где правая часть есть квадратичная форма, заданная в декартовой системе координат . С другой стороны, это выражение определяет линию второго порядка. Ясно что если правая часть последнего равенства представлена суммой квадратов переменных

то имеем канонический вид квадратичной формы.

Оба уравнения будут описывать одну и ту же линию второго порядка, если в форме h сохранен прежний масштаб. Для получения канонического вида H обычно используют характеристическое уравнение. Недостаток такого подхода состоит в том, что неизвестна связь между системами координат и . Образно говоря, мы не знаем расположение линии L в системе координат , если она записана в каноническом виде h . Такой переход можно осуществить поворотом осей системы координат на угол j (рис. VII.1), то есть перейти от координат x , y к x 1 , y 1 по формулам

Для обратного преобразования необходимо заменить угол j
на -j .

Чтобы узнать расположение линии, мы должны найти преобразование координат, приводящее равенство H к виду h . Заметим, что для сохранения масштаба следует перейти к ортонормированной системе координат.

Пример VII.5. Задана квадратичная форма в декартовой системе координат

Требуется привести ее к каноническому виду, то есть записать ее вид в системе и найти линейное преобразование. Получить нормальный вид квадратичной формы.

Решение . Составим симметричную матрицу линейного преобразования (оператора) A

Построим характеристический многочлен и найдем собственные числа и собственные векторы. Затем будем последовательно выполнять задания примера. Имеем

Характеристическое уравнение представляется равенством

Вычислив определитель матрицы, получим многочлен , корни которого , являются собственными числами. Запишем канонический вид формы (VII.7):

Найдем линейное преобразование, то есть установим связь между системами и . Так как корни действительные и различные и нет нулей, то преобразование невырожденное. Найдем собственные векторы в базисе (векторы будем представлять столбцами). Для этого решим систему уравнений

определенную для каждого из собственных чисел.

При , из (VII.8) имеем матричное уравнение

Полагая, с необходимостью, , получим

при , имеем . Первый собственный вектор найден , его длина .

При имеем

или

Прибавляя к первому уравнению второе и, замечая, что если полученное уравнение решать как систему с третьим, то с необходимостью перейдем к первому собственному вектору. Остается составить систему уравнений из суммы двух первых и второго уравнения, тогда получим

Полагая , после упрощений получим систему

Матрицы - удобный инструмент для решения самых различных алгебраических задач. Знание некоторых простых правил для оперирования с ними позволяет приводить матрицы к любым удобным и необходимым в данный момент формам. Часто полезным является использование канонической формы матрицы.

Инструкция

Запомните, что канонический вид матрицы не требует, чтобы на всей главной диагонали стояли единицы. Суть определения заключается в том, что единственные ненулевые элементы матрицы в ее каноническом виде – это единицы. Если они присутствуют, то располагаются на главной диагонали. При этом их количество может варьироваться от нуля до количества строчек в матрице.

Не забывайте, что элементарные преобразования позволяют любую матрицу привести к каноническому виду . Самая большая сложность – интуитивно найти наиболее простую последовательность цепочек действий и не ошибиться в вычислениях.

Выучите основные свойства операций со строчками и столбцами в матрице. К элементарным преобразованиям относят три стандартных преобразования. Это умножение строчки матрицы на любое ненулевое число, суммирование строк (в том числе прибавление к одной другой, умноженной на какое-то число) и их перестановка. Подобные действия позволяют получить матрицу эквивалентную данной. Соответственно, вы можете выполнить такие операции и со столбцами без потери эквивалентности.

Старайтесь не выполнять одновременно сразу несколько элементарных преобразований: продвигайтесь от этапа к этапу, чтобы не допустить случайной ошибки.

Найдите ранг матрицы, чтобы определить количество единиц на главной диагонали: это подскажет вам, какой окончательный вид будет иметь искомая каноническая форма, и избавит от необходимости выполнять преобразования, если требуется просто использовать ее для решения.

Воспользуйтесь методом окаймляющих миноров для того, чтобы выполнить предыдушую рекомендацию. Вычислите минор к-ого порядка, а также все окаймляющие его миноры степени (к+1). Если они равны нулю, то ранг матрицы есть число к. Не забывайте, что минор Мij – это определитель матрицы, получаемой при вычеркивании строки i и столбца j из исходной.

Внимание, только СЕГОДНЯ!

Все интересное

Матрицы, представляющие собой табличную форму записи данных, широко применяются при работе с системами линейных уравнений. Причем число уравнений определяет количество строк матрицы, а количество переменных – порядок ее столбцов. В результате…

Рангом матрицы S называют наибольший из порядков ее миноров, отличных от нуля. Минорами являются определители квадратной матрицы, которая получается из исходной путем выбора произвольных строк и столбцов. Обозначается ранг Rg S, а его вычисление…

Матрица – это математический объект, представляющий собой прямоугольную таблицу. На пересечении столбцов и строк этой таблицы расположены элементы матрицы – целые, действительные или комплексные числа. Размер матрицы устанавливается по количеству ее…

Алгебраическое дополнение – элемент матричной или линейной алгебры, одно из понятий высшей математики наряду с определителем, минором и обратной матрицей. Однако несмотря на кажущуюся сложность, найти алгебраические дополнения нетрудно. Инструкция…

Матрица - это упорядоченная совокупность чисел в прямоугольной таблице, имеющая размерность m строк на n столбцов. Решение сложных систем линейных уравнений основано на вычислении матриц, состоящих из заданных коэффициентов. В общем случае при…

Матричная алгебра – раздел математики, посвященный изучению свойств матриц, их применению для решения сложных систем уравнений, а также правилам действий над матрицами, включая деление. Инструкция 1Существует три действия над матрицами: сложение,…

Алгебраические дополнения – это одно из понятий матричной алгебры, применяемое к элементам матрицы. Нахождение алгебраических дополнений является одним из действий алгоритма определения обратной матрицы, а также операции матричного деления. …

Матрица В считается обратной для матрицы А, если при их умножении образуется единичная матрица Е. Понятие «обратной матрицы» существует только для квадратной матрицы, т.е. матрицы «два на два», «три на три» и т.д.…

Для каждой невырожденной (с определителем |A|, не равном нулю) квадратной матрицы А существует единственная обратная матрица, обозначаемая А^(-1), такая, что (А^(-1))А=А, А^(-1)=Е. Инструкция 1Е называется единичной матрицей. Она состоит из…

Математическая матрица является упорядоченной таблицей элементов с определенным числом строк и столбцов. Чтобы найти решение матрицы, необходимо определить, какое действие требуется над ней выполнить. После этого действуйте согласно имеющимся…

Математика, безусловно, является «королевой» наук. Не каждый человек способен познать всю глубину ее сущности. Математика объединяет в себя множество разделов, и каждый является своеобразным звеном математической цепи. Таким же основным…

Если в любой матрице A взять произвольные k строк и столбцов и составить из элементов этих строк и столбцов подматрицу размера k на k, то такая подматрица называется минором матрицы A. Количество строк и столбцов в наибольшем таком миноре, отличном…

Т" = с (i), Т" = 1………….(i), Т"" = 0…1……….(i) b(λ)……….(j) 1…0……….(j) .

В результате применения правой элементарной операции матрица А(λ) умножается справа на соответствующую матрицу Т.

Заметим, что матрица Т" совпадает с матрицей S", а матрицы Т", Т"" совпадают с матрицами S", S"", если в последних поменять местами индексы i и j. Матрицы типа S", S", S"" (или, что то же, типа Т", Т", Т"") называются элементарными.

Две λ-матрицы А(λ) и B(λ) одинаковых размеров m x n называются эквивалентными, А(λ) ~ B(λ), если от матрицы А(λ) к B(λ) можно перейти при помощи цепочки из конечного числа элементарных преобразований. Отношение эквивалентности обладает тремя основными свойствами:

1) рефлексивность: каждая матрица эквивалентна сама себе А(λ) ~ B(λ);

2) симметрия: если А(λ) ~ B(λ), то B(λ) ~ А(λ);

3) транзитивность: если А(λ) ~ B(λ), и B(λ) ~ С(λ), то А(λ) ~ С(λ).

§2. Канонический вид λ-матрицы

Выше было показано, что отношение эквивалентности транзитивно, симметрично и рефлексивно. Отсюда следует, что совокупность всех λ-матриц данных размеров m x n разбивается на непересекающиеся классы эквивалентных матриц, т.е. на такие классы, что любые две матрицы из одного класса эквивалентны, а из разных классов - не эквивалентны между собой. Возникает вопрос о канонической форме λ-матрицы, характеризующей данный класс эквивалентных λ-матриц.

Канонической диагональной λ-матрицей размеров m x n называется λ-матрица, у которой на главной диагонали стоят многочлены Е1(λ), Е2(λ), …, Ер(λ), где р - меньшее из чисел m и n, причем не равные нулю среди этих многочленов имеют старшие коэффициенты, равные единице, и каждый следующий многочлен делится на предыдущий, все же элементы вне главной диагонали равны нулю.

Т е о р е м а 1. Всякая λ-матрица конечным числом элементарных преобразований может быть приведена к канонической диагональной форме.

Доказательство. Пусть А(λ) - прямоугольная многочленная матрица. Применяя к А(λ) как левые, так и правые элементарные операции приведем к канонической диагональной форме.

Среди всех не равных нулю элементов аіј(λ) матрицы А(λ) возьмем тот элемент, который имеет наименьшую степень относительно λ, и путем соответствующей перестановки строк и столбцов сделаем его элементом а11(λ). После этого найдем частные и остатки от деления многочленов аі1(λ) и а1ј(λ) на а11(λ):

аі1(λ) = а11(λ) qі1(λ) + rі1 (λ), а1ј(λ) = а11(λ) q1ј(λ) + r1ј(λ)

(i = 2, 3, …, m; j = 2, 3, …, n).

Если хотя бы один из остатков rі1(λ), r1ј(λ) (i = 2, …, m; j = 2, …, n), например r1ј (λ), не равен тождественно нулю, то, вычитая из j-го столбца первый столбец, предварительно помноженный на q1ј(λ), мы заменим элемент а1ј(λ) остатком r1ј(λ), который имеет меньшую степень, нежели а11(λ). Тогда мы имеем возможность снова уменьшить степень элемента, стоящего в левом верхнем углу матрицы, поместив на это место элемент с наименьшей степенью относительно λ.

Если же все остатки r21(λ), … rm1(λ); r12(λ), …, r1n(λ) равны тождественно нулю, то, вычитая из i-ой строки первую, помноженную предварительно на qі1(λ) (i = 2, …, m), а из j-го столбца - первый, предварительно помноженный на q1ј(λ) (j = 2, …, n), мы приведем нашу матрицу к виду

а11(λ) 0 … 0

0 а22(λ) … а2n(λ)

….…………………… .

0 аm2(λ) … аmn(λ)

Если при этом хотя бы один из элементов аіј(λ) (i = 2, …, m; j = 2, …, n) не делится без остатка на а11(λ), то, прибавляя к первому столбцу тот столбец, который содержит этот элемент, мы придем к предыдущему случаю и, следовательно, снова сможем заменить элемент а11(λ) многочленом меньшей степени.

Поскольку первоначальный элемент а11(λ) имел определенную степень и процесс уменьшения этой степени не может неограниченно продолжаться, то после конечного числа элементарных операций мы должны получить матрицу вида

(*) 0 b22(λ) … b 2n(λ)

….…………………… ,

0 bm2 (λ) …bmn (λ)

в которой все элементы bіј(λ) делятся без остатка на а1(λ). Если среди этих элементов bіј(λ) имеются не равные тождественно нулю, то продолжая тот же процесс приведения для строк с номерами 2, …, m и столбцов с номерами 2, …, n, мы матрицу (*) приведем к виду

Таким образом мы доказали, что произвольная прямоугольная многочленная матрица А(λ) эквивалентна некоторой канонической диагональной.

Раздел 3. Матрицы

3.1 Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая т строк одинаковой длины (или п столбцов одинаковой длины). Матрица записывается в виде:

или, сокращенно,
, где
(т.е.
) – номер строки,
(т.е.
) – номер столбца.

Матрицу А называют матрицей размера
и пишут
. Числа, составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.

Пример 1. Элемент
расположен в 1-й строке и 2-м столбце, а элементнаходится в 3-й строке и 1-м столбце.

Пример 2. Матрица
имеет размер
, так как она содержит 2 строки и 4 столбца. Матрица
имеет размер
, так как она содержит 3 строки и 2 столбца.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е.
, если
, где
,
.

Матрица, у которой число сток равно числу столбцов, называется квадратной . Квадратную матрицу размера
называют матрицей п-го порядка.

Пример 3. Матрицы ииз примера 2 называются прямоугольными. Матрица
– это квадратная матрица 3-го порядка. Она содержит 3 строки и 3 столбца.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной . Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е .

Пример 4.
– единичная матрица 3-го порядка.

Квадратная матрица называется треугольной , если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой . Обозначается буквой О .

В матричном исчислении матрицы О и Е играют роль 0 и 1 в арифметике.

,
.

Матрица размера
, состоящая из одного числа, отождествляется с этим числом, т.е.
есть 5.

Матрица, полученная из данной, заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначается
. Так, если
, то
если
, то
. Транспонированная матрица обладает следующим свойством:
.

3.2 Операции над матрицами

Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц
и
называется матрица
такая, что
(
,
).

Пример 5. .

Аналогично определяется разность матриц.

Умножение на число

Произведением матрицы
на число k называется матрица
такая, чтоb ij = ka ij (i =
, j =).

Пример 6.
,
,
.

Матрица
называетсяпротивоположной матрице А.

Разность матриц
можно определить так:
.

Операции сложения матриц и умножение матрицы на число обладают следующими свойствами:

где А , В , С – матрицы, α и β – числа.

Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

перестановка местами двух параллельных рядов матрицы;

умножение всех элементов ряда матрицы на число, отличное от нуля;

прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными , если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~В .

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической , например
.

Пример 7. Привести к каноническому виду матрицу
.

Решение: Выполняя элементарные преобразования, получаем

(поменяли местами I и III столбцы) ~
(I строку сложили со II строкой и результат записали во вторую строку; после этого I строку сложили с III строкой и результат записали в третью строку) ~
(I столбец умножили на (-3), сложили со II столбцом и результат записали во II столбец; затем I столбец умножили на (-2), сложили с III столбцом и результат записали в III столбец; после этого I столбец снова умножили на (-2) и сложили с IV столбцом, а результат записали в IV столбец) ~
(III столбец умножили на (-2), сложили со II столбцом и результат записали во II столбец; III столбец разделили на 2 и результат записали в III столбец; III столбец умножили на (-1), сложили с IV столбцом и результат записали в IV столбец) ~
(II строку умножили на 3, сложили с III строкой и результат записали в III строку) ~
(II столбец умножили на (-1), сложили последовательно с III и IV столбцами и результат записали соответственно в III и IV столбец) ~
. Получили матрицу канонического вида.

Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А т×п =(а ij ) на матрицу В п×р =(b jk ) называется матрица С т×р =(с ik ) такая, что

c ik = a i 1 ∙ b 1 k + a i 2 ∙ b 2 k + ∙∙∙+ a in ∙ b nk , где i =
, k =
,

т.е. элемент i -ой строки и k -го столбца матрицы произведения С равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы k -го столбца матрицы В.

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А ∙Е = Е ∙А = А , где А – квадратная матрица, Е – единичная матрица того же размера.

Пример 4.

Матрицы А и В называются перестановочными (коммутирующими ), если АВ =ВА .

Умножение матриц обладает следующими свойствами:

А ∙(В ∙С ) = (А ∙В )∙С ;

А ∙(В + С ) = АВ + АС ;

(А + В )∙С = АС + ВС ;

α (АВ ) = (αА )В ,

если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

(А + В ) Т =А Т + В Т;

(АВ ) Т = В Т ∙А Т.

Если задан многочлен , томатричным многочленом f (A ) называется выражение вида , где
для любого натуральногоп . Значением матричного многочлена f (A ) при заданной матрице А является матрица.

Элемент строки назовем крайним , если он отличен от нуля, а все элементы этой строки, находящиеся левее его, равны нулю. Матрица называется ступенчатой , если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки.

Пример 5. В матрицах А и В отмечены крайние элементы каждой строки:

–не ступенчатая

–ступенчатая

Определение. Многочленной матрицей или -матрицей называется прямоугольная матрица, элементы которой являются многочленами от одного переменногос числовыми коэффициентами.

Над -матрицами можно совершать элементарные преобразования. К ним относятся:

Две -матрицы
и
одинаковых размеров называются эквивалентными:
, если от матрицы
к
можно перейти с помощью конечного числа элементарных преобразований.

Пример. Доказать эквивалентность матриц

Решение.

Умножим вторую строку на (–1) и заметим, что

Множество всех -матриц данных размеров
разбивается на непересекающиеся классы эквивалентных матриц. Матрицы, эквивалентные между собой, образуют один класс, не эквивалентные – другой.

Каждый класс эквивалентных матриц характеризуется канонической, или нормальной, -матрицей данных размеров.

Определение. Канонической, или нормальной, -матрицей размеров
называется-матрица, у которой на главной диагонали стоят многочлены, гдер – меньшее из чисел m и n (
), причем не равные нулю многочлены имеют старшие коэффициенты, равные 1, и каждый следующий многочлен делиться на предыдущий. Все элементы вне главной диагонали равны 0.

Из определения следует, что если среди многочленов имеются многочлены нулевой степени, то они в начале главной диагонали. Если имеются нули, то они стоят в конце главной диагонали.

Матрица
предыдущего примера есть каноническая. Матрица

также каноническая.

Каждый класс -матриц содержит единственную каноническую-матрицу, т.е. каждая-матрица эквивалентна единственной канонической матрице, которая называется канонической формой или нормальной формой данной матрицы.

Многочлены, стоящие на главной диагонали канонической формы данной -матрицы, называются инвариантными множителями данной матрицы.

Один из методов вычисления инвариантных множителей состоит в приведении данной -матрицы к канонической форме.

Так, для матрицы
предыдущего примера инвариантными множителями являются

,
,
,
.

Из сказанного следует, что наличие одной и той же совокупности инвариантных множителей является необходимым и достаточным условием эквивалентности -матриц.

Приведение -матриц к каноническому виду сводится к определению инвариантных множителей

,
;
,

где r – ранг -матрицы;
– наибольший общий делитель миноровk -го порядка, взятый со старшим коэффициентом, равным 1.

Пример. Пусть дана -матрица

Решение. Очевидно, наибольший общий делитель первого порядка D 1 =1, т.е.
.

Определим миноры второго порядка:

Уже этих данных достаточно для того, чтобы сделать вывод: D 2 =1, следовательно,
.

Определяем D 3

Следовательно,
.

Таким образом, канонической формой данной матрицы является следующая -матрица:

Матричным многочленом называется выражение вида

где – переменное;
– квадратные матрицы порядкаn с числовыми элементами.

Если
, тоS называют степенью матричного многочлена, n – порядком матричного многочлена.

Любую квадратичную -матрицу можно представить в виде матричного многочлена. Справедливо, очевидно, и обратное утверждение, т.е. любой матричный многочлен можно представить в виде некоторой квадратной-матрицы.

Справедливость данных утверждений со всей очевидностью вытекает из свойств операций над матрицами. Остановимся на следующих примерах:

Пример. Представить многочленную матрицу

в виде матричного многочлена можно следующим образом

Пример. Матричный многочлен

можно представить в виде следующей многочленной матрицы (-матрицы)

Эта взаимозаменяемость матричных многочленов и многочленных матриц играет существенную роль в математическом аппарате методов факторного и компонентного анализа.

Матричные многочлены одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами. Следует, однако, помнить, что умножение матричных многочленов, вообще говоря, не коммутативно, т.к. не коммутативно умножение матриц.

Два матричных многочлена называются равными, если равны их коэффициенты, т.е. соответствующие матрицы при одинаковых степенях переменного .

Суммой (разностью) двух матричных многочленов
и
называется такой матричный многочлен, у которого коэффициент при каждой степени переменногоравен сумме (разности) коэффициентов при той же степенив многочленах
и
.

Чтобы умножить матричный многочлен
на матричный многочлен
, нужно каждый член матричного многочлена
умножить на каждый член матричного многочлена
, сложить полученные произведения и привести подобные члены.

Степень матричного многочлена – произведения

меньше или равна сумме степеней сомножителей.

Операции над матричными многочленами можно осуществлять с помощью операций над соответствующими -матрицами.

Чтобы сложить (вычесть) матричные многочлены, достаточно сложить (вычесть) соответствующие -матрицы. То же относится к умножению.-матрица произведения матричных многочленов равна произведению-матриц сомножителей.

Пример.

С другой стороны
и
можно записать в виде

Так как умножение матриц не коммутативно, для матричных многочленов определяются два деления с остатком – правое и левое.

Пусть даны два матричных многочлена порядка n

где В 0 – невырожденная матрица.

При делении
на
существует однозначно определенное правое частное
и правый остаток

где степень R 1 меньше степени
, или
(деление без остатка), а также левое частное
и левый остаток

где степень
меньше степени
, или
=0 (деление без остатка).

Обобщённая теорема Безу. При делении матричного многочлена
на многочлен
правый остаток равен правому значению делимого
при
, т.е. матрице

а левый остаток – левому значению делимого
при
, т.е. матрице

Доказательство. Доказательство справедливости обеих формул (3.4.1) и (3.4.2) осуществляется одинаково, непосредственной подстановкой. Докажем одну из них.

Итак, делимое –
, делитель –
, в качестве частного имеем многочлен