Vibrazioni armoniche.

Le oscillazioni sono chiamate processi che differiscono in un grado o nell'altro di ripetizione. Il moto oscillatorio e le onde che provoca sono molto comuni in natura e nella tecnologia. I ponti oscillano sotto l'influenza dei treni che li attraversano, il timpano oscilla, parti degli edifici vibrano, il muscolo cardiaco si contrae ritmicamente.

A seconda della natura fisica del processo ripetitivo, si distinguono le vibrazioni: meccaniche, elettromagnetiche, ecc. Considereremo le vibrazioni meccaniche.

Si consideri il sistema meccanico più semplice costituito da un corpo (palla) di una certa massa m, infilato su un'asta, e una molla con rigidezza k, che lo collega con una parete fissa. Dirigiamo l'asse OX lungo l'asta e l'origine è compatibile con il centro della sfera, a condizione che la molla sia in uno stato non deformato. Spostiamo la palla a una distanza X 0 dalla posizione di equilibrio (vedi Fig. 1). Quindi dal lato della molla agirà sul corpo la forza elastica F=-kX 0 (1). Questa forza, come si può vedere dall'equazione (1), è proporzionale allo spostamento ed è diretta nella direzione opposta allo spostamento. Si chiama forza riparatrice. Inoltre, il sistema avrà una riserva di energia potenziale
. Se il carico viene rilasciato, sotto l'azione di una forza elastica inizierà a muoversi verso la posizione di equilibrio, mentre la sua energia potenziale diminuirà, trasformandosi in energia cinetica.
, la forza di ripristino diminuirà e nella posizione di equilibrio diventerà uguale a zero, ma il corpo nella posizione di equilibrio non si fermerà, ma continuerà a muoversi per inerzia. La sua energia cinetica si trasformerà in potenziale, la forza di ripristino aumenterà, ma la sua direzione cambierà al contrario. Il sistema oscillerà. Con il moto oscillatorio, la posizione del corpo in ogni dato momento è caratterizzata da una distanza dalla posizione di equilibrio, che si chiama spostamento. Tra i vari tipi di oscillazioni, la forma più semplice è l'oscillazione armonica, cioè uno in cui il valore oscillante cambia nel tempo secondo la legge del seno o del coseno.

1. Oscillazioni armoniche non smorzate.

Su un corpo di massa m agisca una forza tendente a riportarlo nella posizione di equilibrio (forza di ripristino) e proporzionale allo spostamento dalla posizione di equilibrio, cioè forza elastica F UPR = -kX . Se non c'è attrito, allora l'equazione della seconda legge di Newton per il corpo è:

;
O
.

Denota
, noi abbiamo
. (1)

L'equazione (1) è un'equazione differenziale omogenea lineare del 2° ordine, con coefficienti costanti. La soluzione dell'equazione (1) sarà la legge delle oscillazioni libere o naturali non smorzate:

,

dove A è il valore della massima deviazione dalla posizione di equilibrio, che è chiamata ampiezza (l'ampiezza è un valore costante e positivo);
- fase di oscillazione; - fase iniziale.

G Le oscillazioni graficamente non smorzate sono mostrate in Fig. 2:

T è il periodo di oscillazione (l'intervallo di tempo di un'oscillazione completa);
, Dove - frequenza circolare o ciclica,
, ν è detta frequenza di oscillazione.

Per trovare la velocità di un punto materiale durante l'oscillazione armonica, devi prendere la derivata dell'espressione per lo spostamento:

Dove
- velocità massima (ampiezza della velocità). Differenziando questa espressione, troviamo l'accelerazione:

Dove
- massima accelerazione.

1. Oscillazioni armoniche smorzate.

In condizioni reali, oltre alla forza di ripristino nel sistema oscillante, agirà la forza di attrito (la forza di resistenza del mezzo), che a basse velocità è proporzionale alla velocità del corpo:
, dove r è il coefficiente di resistenza. Se ci limitiamo a tenere conto della forza di ripristino e della forza di attrito, allora l'equazione del moto assumerà la forma:
O
, dividendo per m, otteniamo:
, denotando
,
, noi abbiamo:
. Questa equazione è chiamata equazione differenziale omogenea lineare del secondo ordine a coefficienti costanti. La soluzione di questa equazione sarà la legge delle oscillazioni libere smorzate, e avrà la seguente forma: .

Si può vedere dall'equazione che l'ampiezza
non è costante, ma dipende dal tempo e decresce esponenzialmente. Per quanto riguarda le oscillazioni non smorzate, il valore ω è chiamato frequenza circolare:
, Dove
- coefficiente di attenuazione;

- fase iniziale.

Le oscillazioni smorzate graficamente sono mostrate in Fig.3.

DI limitare il periodo di oscillazione
O
, che mostra che le oscillazioni nel sistema possono verificarsi solo se la resistenza è trascurabile
. Il periodo di oscillazione è quasi uguale a
.

Con un aumento del coefficiente di attenuazione, il periodo di oscillazione aumenta e a
volge all'infinito. Il movimento cessa di essere periodico. Il sistema rimosso dalla posizione di equilibrio ritorna allo stato di equilibrio senza oscillare. Tale movimento è chiamato aperiodico.

La Figura 4 mostra uno dei casi in cui il sistema ritorna alla posizione di equilibrio durante il moto aperiodico. In accordo con questa curva, la carica sulle membrane delle fibre nervose umane diminuisce.

Per caratterizzare il tasso di smorzamento delle oscillazioni, viene introdotto il concetto di coefficiente di smorzamento
. Troviamo il tempo τ durante il quale l'ampiezza delle oscillazioni diminuirà di un fattore e:

, cioè.

da cui βτ=1, quindi . Il coefficiente di attenuazione è il reciproco dell'intervallo di tempo durante il quale l'ampiezza diminuirà di un fattore e. Il rapporto tra i valori delle ampiezze corrispondenti ai momenti di tempo, che differiscono di un periodo pari a
è chiamato decremento dello smorzamento e il suo logaritmo è chiamato decremento logaritmico dello smorzamento:

.

Grandezze fondamentali, formule e definizioni

Vibrazioni libere non smorzate

1. Periodo T, frequenza  e frequenza di oscillazione ciclica 

,
,

2. Fase di oscillazione , fase iniziale  0

.

3. Equazioni di oscillazioni armoniche libere non smorzate

dove, [x] = m è lo spostamento dell'oggetto oscillante, [A] = m è l'ampiezza delle oscillazioni.

4. La velocità del corpo durante le oscillazioni armoniche

.

5. Accelerazione di un corpo durante le oscillazioni armoniche

6. Equazione differenziale delle oscillazioni armoniche

.

7. La forza di ripristino che causa il processo oscillatorio

,

dove m è la massa del corpo oscillante.

8. Caratteristiche cinematiche del moto oscillatorio

9. Significato fisico della fase iniziale delle oscillazioni  0

10. Forza di ripristino per oscillazioni armoniche elastiche

,

dove k è la rigidezza o il coefficiente della forza quasi elastica.

11. La relazione tra rigidità e frequenza ciclica, frequenza e periodo di oscillazione

.

12. Energia cinetica delle vibrazioni K

,

.

13. Energia potenziale delle vibrazioni 

,

.

14. La legge di conservazione dell'energia per una forza quasi elastica conservativa

15. Il processo di transizione energetica durante le vibrazioni da un tipo all'altro con una frequenza di 2

16. Valore medio della cinetica e potenziale<П>energia

.

17. Equazione differenziale delle piccole oscillazioni di un pendolo matematico sin  

,

,

 il momento d'inerzia del peso del pendolo m con la lunghezza del filo di sospensione attorno ad un asse passante perpendicolare al piano di oscillazione attraverso il punto di sospensione,
 frequenza ciclica delle oscillazioni di un pendolo matematico.

18. Equazione delle oscillazioni di un pendolo matematico

.

19. Il periodo di oscillazione di un pendolo matematico

.

20. Equazione differenziale delle oscillazioni di un pendolo fisico

,

dove J è il momento di inerzia del pendolo rispetto all'asse perpendicolare al piano di oscillazione e passante per il punto di sospensione, è la distanza tra il punto di sospensione e il baricentro del pendolo.

21. Frequenza ciclica  di piccole oscillazioni di un pendolo fisico, quando sin  

.

22. Il periodo di piccole oscillazioni di un pendolo fisico

,

Dove
è la lunghezza ridotta del pendolo fisico.

24. Equazione differenziale delle oscillazioni lineari libere della massa m connessa ad una molla di rigidezza k

.

25. Il periodo di oscillazione del carico sulla molla

.

26. Parametri di vibrazione torsionale

,

dove C è la rigidezza dell'elemento elastico del pendolo di torsione, per un'asta omogenea

,

dove G è il modulo di taglio, d è il diametro dell'asta, è la lunghezza dell'asta.

Oscillazioni libere smorzate

27. La forza di resistenza, proporzionale alla velocità di movimento

,

dove r è il coefficiente di resistenza.

28. Equazione differenziale delle oscillazioni smorzate

Dove
- coefficiente di attenuazione,
 frequenza ciclica delle oscillazioni naturali non smorzate.

29. Equazione delle oscillazioni smorzate

dove  0  frequenza delle oscillazioni naturali.

30. Rappresentazione grafica delle oscillazioni smorzate

31. Periodo di oscillazioni smorzate

.

.

33. Decremento logaritmico 

.

34. Fattore di qualità del sistema oscillatorio Q

,

dove N e è il numero di oscillazioni complete durante il tempo  = 1/ durante il quale l'ampiezza A(t) diminuisce di e volte.

35. Energia delle oscillazioni smorzate

.

36. Variazione dell'energia delle oscillazioni smorzate nel tempo

.

37. Variazione dell'energia delle oscillazioni smorzate per piccoli valori del coefficiente di resistenza

,

dove E 0 è l'energia delle oscillazioni smorzate nel momento iniziale del tempo.

38. Perdita di energia delle oscillazioni smorzate durante un periodo

.

Vibrazioni forzate

39. Forza periodica esterna che agisce su un sistema oscillatorio

,

dove F 0 è il valore di ampiezza della forza.

40. Equazione differenziale delle oscillazioni forzate

Dove
,
,
.

41. L'equazione delle vibrazioni forzate

,

Dove
- ampiezza delle oscillazioni forzate,

 fase iniziale di oscillazioni forzate.

42. Equazione delle vibrazioni forzate con lo smorzamento

43. Frequenza ciclica risonante delle oscillazioni forzate

.

44. Ampiezza delle vibrazioni risonanti

.

45. Dipendenza dell'ampiezza delle oscillazioni forzate dalla frequenza della forza motrice

46. ​​​​Fattore di qualità delle oscillazioni forzate a basso smorzamento

,

Dove
 spostamento dalla posizione di equilibrio sotto l'azione di una forza costante F 0 .

47. Il processo di stabilire oscillazioni forzate a <<  0

48. Il processo di stabilire oscillazioni forzate a  >>  0

49. Stabilimento di oscillazioni forzate a  0  

50. Istituzione di oscillazioni forzate a  0   per diversi valori del fattore di qualità del sistema oscillatorio

Aggiunta di vibrazioni armoniche

51. Il risultato della somma di due (figura a sinistra) e tre oscillazioni

52. Il risultato dell'aggiunta di due oscillazioni significativamente diverse in frequenza

53. Somma di due oscillazioni con le stesse frequenze che si verificano nella stessa direzione

,
,

54. Aggiunta di due vibrazioni con le stesse frequenze e le stesse ampiezze A 1 \u003d A 2

,
.

55. Somma di due oscillazioni armoniche con frequenze diverse  1 e  2 che si verificano nella stessa direzione

,

,
,

,

56. Il periodo risultante quando si aggiungono due oscillazioni con frequenze leggermente diverse (battiti)

.

57. Sovrapposizione di oscillazioni reciprocamente perpendicolari (figure di Lissajous) con un rapporto di frequenza m: n per diversa differenza di fase 

Onde in un mezzo elastico

58. La relazione tra la velocità di fase di un'onda c elastica, la sua frequenza , la lunghezza d'onda  e il periodo T

.

59. Velocità di fase di un'onda elastica trasversale nei solidi

,

dove F è la forza di tensione di una corda, un'asta, un filo, ecc.,  è la densità del materiale di cui è composto il corpo, s è l'area della sezione trasversale.

60. Velocità di fase di un'onda longitudinale in un solido

,

dove E Y  modulo di Young.

61. Velocità di fase di un'onda elastica nei liquidi

,

dove  è la compressibilità del liquido,  è la densità del liquido.

62. Velocità di fase di un'onda longitudinale in un gas a pressione p

,

dove  è l'indice adiabatico,  è la densità del gas, R è la costante universale dei gas, T è la temperatura assoluta.

63. Densità di energia di un'onda elastica

,

dove A è l'ampiezza delle oscillazioni delle particelle del mezzo,  è la frequenza ciclica, dÅ è l'energia dell'onda nel volume dV.

64. Flusso di energia F E, ad es. la quantità di energia che passa attraverso l'area s nel tempo 

.

65. Potenza di un'onda elastica

.

66. Intensità dell'onda elastica

.

67. Equazione delle onde

,

dove  è lo spostamento trasversale istantaneo dalla posizione di equilibrio x, c è la velocità di fase dell'onda.

68. Le onde stazionarie si formano quando due onde della stessa ampiezza, lunghezza e frequenza si propagano, in particolare, in un mezzo elastico in direzioni opposte

,

,

,

dove   spostamento, A, B  valori costanti,   lunghezza d'onda.

onde acustiche

69. Equazione delle onde acustiche

70. Il valore massimo della velocità vibrazionale

.

71. Valore effettivo della velocità vibrazionale

.

72. Valore istantaneo della pressione acustica

.

73. Valore di picco della pressione acustica

.

74. Intensità (forza del suono) di un'onda acustica

75. Livello di pressione acustica

,

dove J 0 \u003d 10 - 12 W / m 2 - soglia uditiva standard.

76. Effetto Doppler

,

dove  è la frequenza del suono percepito,  0 è la frequenza del suono emesso, s è la velocità del suono, u 1 è la velocità del ricevitore, u 2 è la velocità dell'emettitore.

Vibrazioni elettromagnetiche

1. L'equazione del circuito oscillatorio

,

dove L è l'induttanza del circuito, C è la capacità del circuito, q è la carica sulle piastre del condensatore, R è la resistenza attiva del circuito,  è la forza elettromotrice della sorgente di corrente formule ... casuale le quantità. Principale compito... simile all'equazione gratuitonon smorzatoesitazione(2) dove...

Legge fondamentale dell'elettrostatica

Legge

Carica. Di base legge dell'elettrostatica... particella dentro gratuitoesitazione. Elementare... le quantità: r=R/cosα, dl=rdα/cosα. Sostituzione in formula ... non smorzatofluttuazioni di contorno. fluttuazioni chiamati movimenti o processi che sono caratterizzati da certo ...

ISBN 5-06-003634-0

Esercitazione

Velocità di rotazione. paragonabile principalele quantità ed equazioni, ... attenuazione, 0 - frequenza ciclica gratuitonon smorzatoesitazione lo stesso sistema oscillatorio, t... m/s). Qual è la precisione definizioni coordinate elettroniche? Di formula(215.4), v. ...

Laboratorio di laboratorio (2)

Lavoro di laboratorio

... ... ,%. Domande di controllo 1. fluttuazioni. Gratuitofluttuazioni. 2. Gratuitonon smorzatofluttuazioni. 3. Equazioni gratuitonon smorzatoesitazione(equazione differenziale e sua soluzione). 4. Le quantità caratterizzante fluttuazioni: ampiezza, frequenza...

1. 
   Elementi di biomeccanica 5
2. 
   Vibrazioni meccaniche 14
3. 
   Biofisica dell'udito. Suono. Ultrasuoni 17
4. 
   Biofisica della circolazione sanguigna 21
5. 
   Proprietà elettriche di tessuti e organi 28
6. 
   Elettrocardiografia. Reografia 33
7. 
   Fondamenti di elettroterapia 36
8. 
   Biofisica della visione. Strumenti ottici 40

1.9 Radiazione termica e sue caratteristiche 45

2.0 Raggi X 49

2.1 Elementi di fisica delle radiazioni. Fondamenti di dosimetria 54

3. La diadinamica è uno dei dispositivi di elettroterapia più famosi che utilizza l'effetto analgesico e antispasmodico delle correnti a bassa frequenza per scopi medicinali, ad esempio per migliorare la circolazione sanguigna nel corpo. La procedura è prescritta esclusivamente da un medico, la durata è di 3-6 minuti (per condizioni acute ogni giorno, per malattie croniche 3 volte a settimana per 5-6 minuti).

Indicazioni: malattie dell'apparato muscolo-scheletrico, in particolare dolori articolari e

colonna vertebrale

L'elettrosleep è un metodo di elettroterapia che utilizza correnti pulsate di bassa o frequenza audio (1-130 Hz), forma rettangolare, bassa potenza (fino a 2-3 mA) e tensione (fino a 50 V), causando sonnolenza, sonnolenza e quindi dormire di varia profondità e durata.
Indicazioni: malattie degli organi interni (malattia coronarica cronica, ipertensione, ipotensione, reumatismi, ulcera peptica dello stomaco e del duodeno, ipotiroidismo, gotta), malattie del sistema nervoso (aterosclerosi dei vasi cerebrali nella fase iniziale, cerebropatia traumatica, sindrome ipotalamica, emicrania, nevrastenia, sindrome astenica, psicosi maniaco-depressiva, schizofrenia).

L'amplipulse terapia è una delle metodiche di elettroterapia basate sull'utilizzo di correnti sinusoidali modulate a scopo terapeutico, profilattico e riabilitativo.

Oscillazioni armoniche continue

Le vibrazioni armoniche vengono eseguite sotto l'azione di forze elastiche o quasi elastiche (simili a quelle elastiche), descritte dalla legge di Hooke:

Dove ^ Fè la forza dell'elasticità;

X – pregiudizio;

Kè il coefficiente di elasticità o rigidità.

Secondo la seconda legge di Newton
, Dove UN- accelerazione, UN =
.

Dividiamo l'equazione (1) per la massa m e introduciamo la notazione
, otteniamo l'equazione nella forma:

(2).

Equazione (2) - equazione differenziale delle oscillazioni armoniche non smorzate.

La sua soluzione ha la forma: o .
^ Caratteristiche delle oscillazioni armoniche non smorzate:

X- compensare; UN- ampiezza; T- periodo; – frequenza; è la frequenza ciclica, - velocità; - accelerazione, - fase; 0 - fase iniziale, E- piena energia.

Formule:

è il numero di vibrazioni, - il tempo durante il quale vengono eseguite N oscillazioni;

, ; O ;

O ;

– fase di oscillazioni armoniche non smorzate;

è l'energia totale delle oscillazioni armoniche.

Oscillazioni armoniche smorzate

Nei sistemi reali che partecipano al moto oscillatorio, le forze di attrito (resistenza) sono sempre presenti:

, è il coefficiente di resistenza aerodinamica;
- velocità.

.

Quindi scriviamo la seconda legge di Newton:

(2)

Introduciamo la notazione ,
, Dove è il coefficiente di attenuazione.

L'equazione (2) può essere scritta come:

(3)

Equazione (3) - equazione differenziale dell'oscillazione smorzata.

La sua soluzione è dove

è l'ampiezza di oscillazione al momento iniziale del tempo;

è la frequenza ciclica delle oscillazioni smorzate.

L'ampiezza di oscillazione cambia secondo la legge esponenziale:

.

Riso. 11. Grafico X= F(T)

Riso. 12. Grafico UN T = F(T)

Caratteristiche:

1)
è il periodo delle oscillazioni smorzate; 2) è la frequenza delle oscillazioni smorzate; è la frequenza naturale del sistema oscillatorio;

3) decremento dello smorzamento logaritmico (caratterizza il tasso di diminuzione dell'ampiezza):
.

^ Vibrazioni forzate

Per ottenere oscillazioni non smorzate è necessaria l'azione di una forza esterna il cui lavoro compenserebbe la diminuzione di energia del sistema oscillante causata dalle forze di resistenza. Tali oscillazioni sono chiamate forzate.

Legge del cambiamento della forza esterna:
, Dove è l'ampiezza della forza esterna.

Scriviamo la seconda legge di Newton nella forma

Introduciamo la notazione
.

L'equazione delle oscillazioni forzate ha la forma:

La soluzione di questa equazione in stato stazionario è:

,

Dove

(4)

è la frequenza delle oscillazioni forzate.

Dalla formula (4), quando
, l'ampiezza raggiunge il suo valore massimo. Questo fenomeno si chiama risonanza.

^ 1.3 Biofisica dell'udito. Suono. Ultrasuoni.

Ondaè il processo di propagazione delle oscillazioni in un mezzo elastico.

equazione delle onde esprime la dipendenza dello spostamento di un punto oscillante che partecipa al processo ondulatorio dalla coordinata della sua posizione e tempo di equilibrio: S = F (X ; T).

Se S e X sono dirette lungo la stessa retta, allora l'onda longitudinale, se sono reciprocamente perpendicolari, allora l'onda trasversale.

L'equazione nel punto "0" ha la forma
. Il fronte d'onda raggiungerà il punto "x" con un ritardo nel tempo
.

equazione delle onde ha la forma
.

Caratteristiche dell'onda:

S- compensare, UN– ampiezza, – frequenza, T– periodo, – frequenza ciclica, - velocità.

è la fase dell'onda, è la lunghezza d'onda.

Lunghezza d'ondaè la distanza tra due punti le cui fasi nello stesso istante di tempo differiscono di
.

^ Fronte d'onda- un insieme di punti che hanno la stessa fase allo stesso tempo.

Flusso di energiaè uguale al rapporto tra l'energia trasportata dalle onde attraverso una certa superficie e il tempo durante il quale questa energia è stata trasferita:

,
.

Intensità:
, – piazza,
.

Viene chiamato il vettore di intensità che mostra la direzione di propagazione dell'onda ed è uguale al flusso di energia dell'onda attraverso un'area unitaria perpendicolare a questa direzione Vettore umov.

è la densità della materia.
onde sonore

Suonoè un'onda meccanica la cui frequenza si trova all'interno di ,
- infrasuoni,
– ecografia.

Ci sono toni musicali (questa è un'onda monocromatica con una frequenza o costituita da onde semplici con un insieme discreto di frequenze - un tono complesso).

^ Rumoreè un'onda meccanica con uno spettro continuo e ampiezze e frequenze che cambiano caoticamente.

Esso ha
, in cui
.

. 1 Decibel (dB) o 1 sfondo = 0,1 B.

La dipendenza del volume dalla frequenza viene presa in considerazione utilizzando curve di volume uguale ottenute sperimentalmente e viene utilizzata per valutare i difetti dell'udito. Viene chiamato il metodo per misurare l'acuità dell'udito audiometria. Viene chiamato lo strumento per misurare il volume fonometro. Il livello del volume del suono dovrebbe essere di 40 - 60 dB.

1. Fluttuazioni. oscillazioni periodiche. Vibrazioni armoniche.

2. Vibrazioni libere. Oscillazioni non smorzate e smorzate.

3. Vibrazioni forzate. Risonanza.

4. Confronto di processi oscillatori. Energia delle oscillazioni armoniche non smorzate.

5. Auto-oscillazioni.

6. Oscillazioni del corpo umano e loro registrazione.

7. Concetti base e formule.

8. Compiti.

1.1. Fluttuazioni. oscillazioni periodiche.

Vibrazioni armoniche

fluttuazioni vengono chiamati processi che differiscono in vari gradi di ripetizione.

ricorrente i processi si verificano continuamente all'interno di qualsiasi organismo vivente, ad esempio: contrazioni cardiache, funzionalità polmonare; tremiamo quando abbiamo freddo; sentiamo e parliamo grazie alle vibrazioni dei timpani e delle corde vocali; Quando camminiamo, le nostre gambe compiono movimenti oscillatori. Gli atomi che ci fanno vibrare. Il mondo in cui viviamo è sorprendentemente soggetto a fluttuazioni.

A seconda della natura fisica del processo ripetitivo, si distinguono le oscillazioni: meccaniche, elettriche, ecc. Questa conferenza discute vibrazioni meccaniche.

Fluttuazioni periodiche

periodico chiamate tali oscillazioni in cui tutte le caratteristiche del movimento si ripetono dopo un certo periodo di tempo.

Per le oscillazioni periodiche, vengono utilizzate le seguenti caratteristiche:

periodo di oscillazione T, pari al tempo durante il quale avviene un'oscillazione completa;

frequenza di oscillazioneν, pari al numero di oscillazioni al secondo (ν = 1/T);

ampiezza di oscillazione A, pari allo spostamento massimo dalla posizione di equilibrio.

Vibrazioni armoniche

Un posto speciale tra le fluttuazioni periodiche è occupato da armonico fluttuazioni. La loro importanza è dovuta ai seguenti motivi. In primo luogo, le oscillazioni in natura e tecnologia hanno spesso un carattere molto vicino all'armonico e, in secondo luogo, i processi periodici di forma diversa (con una diversa dipendenza dal tempo) possono essere rappresentati come una sovrapposizione di diverse oscillazioni armoniche.

Vibrazioni armoniche- si tratta di oscillazioni in cui il valore osservato cambia nel tempo secondo la legge del seno o del coseno:

In matematica vengono chiamate funzioni di questo tipo armonico, pertanto, le oscillazioni descritte da tali funzioni sono anche chiamate armoniche.

La posizione di un corpo che compie un moto oscillatorio è caratterizzata da Dislocamento sulla posizione di equilibrio. In questo caso le grandezze della formula (1.1) hanno il seguente significato:

X- pregiudizio corpo al tempo t;

UN - ampiezza fluttuazioni pari allo spostamento massimo;

ω - frequenza circolare oscillazioni (il numero di oscillazioni effettuate in 2 π secondi), correlata alla frequenza di oscillazione dal rapporto

φ = ( t +φ 0) - fase fluttuazioni (al tempo t); φ 0 - fase iniziale oscillazioni (a t = 0).

Riso. 1.1. Grafici di offset rispetto al tempo per x(0) = A e x(0) = 0

1.2. Vibrazioni libere. Oscillazioni non smorzate e smorzate

gratuito O Proprio chiamò tali oscillazioni che si verificano in un sistema lasciato a se stesso, dopo che è stato portato fuori equilibrio.

Un esempio è l'oscillazione di una sfera sospesa su un filo. Per provocare vibrazioni, è necessario spingere la palla o, spostandola di lato, rilasciarla. Quando viene spinta, la palla viene informata cinetico energia, e in caso di deviazione - potenziale.

Le oscillazioni libere vengono eseguite a causa della riserva di energia iniziale.

Vibrazioni libere non smorzate

Le oscillazioni libere possono essere smorzate solo in assenza di forza di attrito. Altrimenti, la fornitura iniziale di energia verrà spesa per superarla e la gamma di oscillazioni diminuirà.

Ad esempio, si considerino le vibrazioni di un corpo sospeso su una molla priva di peso, che si verificano dopo che il corpo è stato deviato verso il basso e poi rilasciato (Fig. 1.2).

Riso. 1.2. Vibrazioni di un corpo su una molla

Dal lato della molla allungata, il corpo agisce forza elastica F proporzionale alla quantità di spostamento X:

Viene chiamato il fattore costante k indice di rigidezza e dipende dalle sue dimensioni e dal materiale. Il segno "-" indica che la forza elastica è sempre diretta nella direzione opposta alla direzione dello spostamento, cioè alla posizione di equilibrio.

In assenza di attrito, la forza elastica (1.4) è l'unica forza che agisce sul corpo. Secondo la seconda legge di Newton (ma = F):

Dopo aver trasferito tutti i termini sul lato sinistro e diviso per la massa corporea (m), otteniamo un'equazione differenziale per le oscillazioni libere in assenza di attrito:

Il valore ω 0 (1.6) è risultato essere uguale alla frequenza ciclica. Questa frequenza è chiamata Proprio.

Pertanto, le vibrazioni libere in assenza di attrito sono armoniche se, deviando dalla posizione di equilibrio, forza elastica(1.4).

Circolare propria la frequenza è la caratteristica principale delle oscillazioni armoniche libere. Questo valore dipende solo dalle proprietà del sistema oscillante (nel caso in esame, dalla massa del corpo e dalla rigidezza della molla). In quanto segue, il simbolo ω 0 sarà sempre usato per denotare frequenza circolare naturale(cioè, la frequenza alla quale le vibrazioni si verificherebbero in assenza di attrito).

Ampiezza delle vibrazioni libereè determinato dalle proprietà del sistema oscillatorio (m, k) e dall'energia ad esso impartita nel momento iniziale del tempo.

In assenza di attrito, in altri sistemi si verificano anche oscillazioni libere vicine all'armonica: pendoli matematici e fisici (la teoria di questi problemi non è considerata) (Fig. 1.3).

Pendolo matematico- un piccolo corpo (punto materiale) sospeso su un filo senza peso (Fig. 1.3 a). Se il filo viene deviato dalla posizione di equilibrio di un angolo α piccolo (fino a 5°) e rilasciato, allora il corpo oscillerà con un periodo determinato dalla formula

dove L è la lunghezza del filo, g è l'accelerazione di caduta libera.

Riso. 1.3. Pendolo matematico (a), pendolo fisico (b)

pendolo fisico- un corpo rigido che oscilla sotto l'azione della gravità attorno ad un asse orizzontale fisso. La figura 1.3 b mostra schematicamente un pendolo fisico sotto forma di un corpo di forma arbitraria, deviato dalla posizione di equilibrio di un angolo α. Il periodo di oscillazione di un pendolo fisico è descritto dalla formula

dove J è il momento di inerzia del corpo rispetto all'asse, m è la massa, h è la distanza tra il baricentro (punto C) e l'asse di sospensione (punto O).

Il momento d'inerzia è una quantità che dipende dalla massa del corpo, dalle sue dimensioni e dalla posizione rispetto all'asse di rotazione. Il momento di inerzia viene calcolato utilizzando formule speciali.

Vibrazioni smorzate libere

Le forze di attrito che agiscono nei sistemi reali modificano in modo significativo la natura del movimento: l'energia di un sistema oscillatorio diminuisce costantemente e le oscillazioni dissolvenza o non si verificano affatto.

La forza di resistenza è diretta nella direzione opposta al movimento del corpo, ea velocità non molto elevate è proporzionale alla velocità:

Un grafico di tali fluttuazioni è mostrato in Fig. 1.4.

Come caratteristica del grado di attenuazione viene utilizzata una grandezza adimensionale, chiamata decremento logaritmico dello smorzamentoλ.

Riso. 1.4. Spostamento in funzione del tempo per oscillazioni smorzate

Decremento logaritmico dello smorzamentoè uguale al logaritmo naturale del rapporto tra l'ampiezza dell'oscillazione precedente e l'ampiezza dell'oscillazione successiva.

dove i è il numero ordinale dell'oscillazione.

È facile vedere che il decremento logaritmico dello smorzamento si trova con la formula

Forte attenuazione. A

se la condizione β ≥ ω 0 è soddisfatta, il sistema ritorna alla posizione di equilibrio senza oscillare. Tale movimento è chiamato aperiodico. La Figura 1.5 mostra due possibili modi per tornare alla posizione di equilibrio durante il moto aperiodico.

Riso. 1.5. moto aperiodico

1.3. Vibrazioni forzate, risonanza

Le vibrazioni libere in presenza di forze di attrito vengono smorzate. Le oscillazioni continue possono essere create con l'aiuto di un'azione esterna periodica.

costretto tali oscillazioni sono chiamate, durante le quali il sistema oscillante è esposto a una forza periodica esterna (si chiama forza motrice).

Lascia che la forza motrice cambi secondo la legge armonica

Il grafico delle oscillazioni forzate è mostrato in Fig. 1.6.

Riso. 1.6. Grafico dello spostamento in funzione del tempo per le vibrazioni forzate

Si può vedere che l'ampiezza delle oscillazioni forzate raggiunge gradualmente un valore costante. Le oscillazioni forzate costanti sono armoniche e la loro frequenza è uguale alla frequenza della forza motrice:

L'ampiezza (A) delle oscillazioni forzate costanti si trova con la formula:

Risonanzaè chiamato il raggiungimento dell'ampiezza massima delle oscillazioni forzate a un certo valore della frequenza della forza motrice.

Se la condizione (1.18) non è soddisfatta, la risonanza non si verifica. In questo caso, all'aumentare della frequenza della forza motrice, l'ampiezza delle oscillazioni forzate diminuisce in modo monotono, tendendo a zero.

La dipendenza grafica dell'ampiezza A delle oscillazioni forzate sulla frequenza circolare della forza motrice a diversi valori del coefficiente di smorzamento (β 1 > β 2 > β 3) è mostrata in fig. 1.7. Un tale insieme di grafici è chiamato curve di risonanza.

In alcuni casi, un forte aumento dell'ampiezza delle oscillazioni alla risonanza è pericoloso per la forza del sistema. Ci sono casi in cui la risonanza ha portato alla distruzione delle strutture.

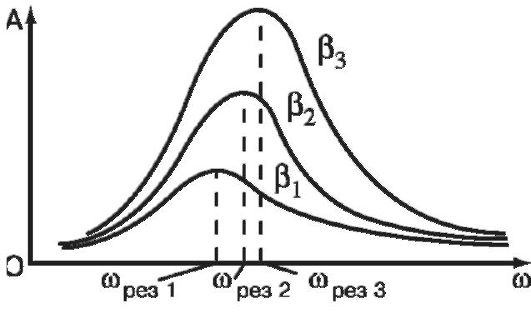Riso. 1.7. Curve di risonanza

1.4. Confronto di processi oscillatori. Energia delle oscillazioni armoniche non smorzate

La Tabella 1.1 presenta le caratteristiche dei processi oscillatori considerati.

Tabella 1.1. Caratteristiche delle vibrazioni libere e forzate

Energia delle oscillazioni armoniche non smorzate

Un corpo che esegue oscillazioni armoniche ha due tipi di energia: l'energia cinetica del movimento E k \u003d mv 2 / 2 e l'energia potenziale E p associata all'azione di una forza elastica. È noto che sotto l'azione della forza elastica (1.4) l'energia potenziale del corpo è determinata dalla formula E p = kx 2 /2. Per oscillazioni non smorzate X= A cos(ωt), e la velocità del corpo è determinata dalla formula v= - A ωsin(ωt). Da ciò si ottengono espressioni per le energie di un corpo che esegue oscillazioni non smorzate:

L'energia totale del sistema in cui si verificano oscillazioni armoniche non smorzate è la somma di queste energie e rimane invariata:

Qui m è la massa del corpo, ω e A sono la frequenza circolare e l'ampiezza delle oscillazioni, k è il coefficiente di elasticità.

1.5. Auto-oscillazioni

Esistono sistemi che regolano essi stessi il rifornimento periodico dell'energia persa e quindi possono fluttuare a lungo.

Auto-oscillazioni- oscillazioni non smorzate supportate da una fonte esterna di energia, la cui erogazione è regolata dal sistema oscillatorio stesso.

I sistemi in cui si verificano tali oscillazioni sono chiamati auto oscillante. L'ampiezza e la frequenza delle auto-oscillazioni dipendono dalle proprietà del sistema auto-oscillante stesso. Il sistema auto-oscillatorio può essere rappresentato dal seguente schema:

In questo caso il sistema oscillatorio stesso, attraverso un canale di retroazione, agisce sul regolatore di energia, informandolo sullo stato del sistema.

Feedback chiamato l'impatto dei risultati di qualsiasi processo sul suo corso.

Se un tale impatto porta ad un aumento dell'intensità del processo, viene chiamato il feedback positivo. Se l'impatto porta a una diminuzione dell'intensità del processo, viene chiamato il feedback negativo.

In un sistema auto-oscillante possono essere presenti feedback sia positivi che negativi.

Un esempio di sistema auto-oscillante è un orologio in cui il pendolo riceve degli urti dovuti all'energia di un peso sollevato o di una molla attorcigliata, e questi urti si verificano in quei momenti in cui il pendolo passa per la posizione centrale.

Esempi di sistemi biologici auto-oscillatori sono organi come il cuore ei polmoni.

1.6. Oscillazioni del corpo umano e loro registrazione

L'analisi delle oscillazioni create dal corpo umano o dalle sue singole parti è ampiamente utilizzata nella pratica medica.

Movimenti oscillatori del corpo umano quando si cammina

La deambulazione è un complesso processo locomotore periodico risultante dall'attività coordinata dei muscoli scheletrici del tronco e degli arti. L'analisi del processo di deambulazione fornisce molte caratteristiche diagnostiche.

Una caratteristica della deambulazione è la periodicità della posizione di appoggio con un piede (periodo di appoggio singolo) o due gambe (periodo di appoggio doppio). Normalmente, il rapporto di questi periodi è 4:1. Quando si cammina, c'è uno spostamento periodico del centro di massa (CM) lungo l'asse verticale (normalmente di 5 cm) e una deviazione laterale (normalmente di 2,5 cm). In questo caso, il CM si muove lungo una curva, che può essere approssimativamente rappresentata da una funzione armonica (Fig. 1.8).

Riso. 1.8. Spostamento verticale del CM del corpo umano durante la deambulazione

Complessi movimenti oscillatori mantenendo la posizione verticale del corpo.

Una persona in piedi verticalmente sperimenta complesse oscillazioni del comune centro di massa (MCM) e centro di pressione (CP) dei piedi sul piano di appoggio. Sulla base dell'analisi di queste fluttuazioni statocinesimetria- un metodo per valutare la capacità di una persona di mantenere una postura eretta. Mantenendo la proiezione GCM entro le coordinate del confine dell'area di supporto. Questo metodo viene implementato utilizzando un analizzatore stabilometrico, la cui parte principale è una piattaforma stabilometrica su cui il soggetto si trova in posizione verticale. Le oscillazioni effettuate dalla PC del soggetto mantenendo una postura verticale vengono trasmesse allo stabiloplatform e registrate da appositi estensimetri. I segnali dell'estensimetro vengono trasmessi al dispositivo di registrazione. Allo stesso tempo, viene registrato statocinesigramma - la traiettoria del movimento del soggetto del test su un piano orizzontale in un sistema di coordinate bidimensionale. Secondo lo spettro armonico statocinesigrammiè possibile giudicare le caratteristiche della verticalizzazione nella norma e con deviazioni da essa. Questo metodo consente di analizzare gli indicatori di stabilità statocinetica (SCR) di una persona.

Vibrazioni meccaniche del cuore

Esistono vari metodi per studiare il cuore, che si basano su processi periodici meccanici.

Ballistocardiografia(BCG) - un metodo per studiare le manifestazioni meccaniche dell'attività cardiaca, basato sulla registrazione dei micromovimenti del polso del corpo, causati dall'espulsione del sangue dai ventricoli del cuore in grandi vasi. Questo dà origine al fenomeno ritorna. Il corpo umano è posto su una speciale piattaforma mobile situata su un massiccio tavolo fisso. La piattaforma come risultato del rinculo entra in un complesso movimento oscillatorio. La dipendenza dello spostamento della piattaforma con il corpo nel tempo è chiamata ballistocardiogramma (Fig. 1.9), la cui analisi consente di giudicare il movimento del sangue e lo stato dell'attività cardiaca.

Apexcardiografia(AKG) - un metodo di registrazione grafica delle oscillazioni a bassa frequenza del torace nell'area del battito dell'apice, causate dal lavoro del cuore. La registrazione dell'apicecardiogramma viene eseguita, di regola, su un elettrocardiogramma multicanale.

Riso. 1.9. Registrazione di un ballistocardiogramma

grafico utilizzando un sensore piezocristallino, che è un convertitore di vibrazioni meccaniche in vibrazioni elettriche. Prima della registrazione sulla parete anteriore del torace, il punto di massima pulsazione (battito apicale) è determinato dalla palpazione, in cui è fissato il sensore. Sulla base dei segnali del sensore, viene creato automaticamente un apiccardiogramma. Viene eseguita un'analisi dell'ampiezza dell'ACG - le ampiezze della curva vengono confrontate in diverse fasi del lavoro del cuore con una deviazione massima dalla linea zero - il segmento EO, considerato al 100%. La Figura 1.10 mostra l'apicecardiogramma.

Riso. 1.10. Registrazione dell'apicecardiogramma

Cinetocardiografia(KKG) - un metodo per registrare le vibrazioni a bassa frequenza della parete toracica, causate dall'attività cardiaca. Il cinetocardiogramma differisce dall'apexcardiogramma: il primo registra i movimenti assoluti della parete toracica nello spazio, il secondo registra le fluttuazioni degli spazi intercostali rispetto alle costole. Questo metodo determina lo spostamento (KKG x), la velocità di movimento (KKG v) e l'accelerazione (KKG a) per le oscillazioni del torace. La Figura 1.11 mostra un confronto di vari kinetocardiogrammi.

Riso. 1.11. Registrazione cinetocardiogrammi di spostamento (x), velocità (v), accelerazione (a)

Dinamocardiografia(DKG) - un metodo per valutare il movimento del centro di gravità del torace. Il dinamocardiografo consente di registrare le forze che agiscono dal torace umano. Per registrare un dinamocardiogramma, il paziente viene posizionato sul tavolo sdraiato sulla schiena. Sotto il petto è presente un dispositivo percettivo, costituito da due lastre metalliche rigide di 30x30 cm, tra le quali sono montati elementi elastici con estensimetri. Cambiando periodicamente in grandezza e luogo di applicazione, il carico che agisce sul dispositivo ricevente è composto da tre componenti: 1) una componente costante - la massa del torace; 2) variabile - effetto meccanico dei movimenti respiratori; 3) variabile - processi meccanici che accompagnano la contrazione cardiaca.

La registrazione del dinamocardiogramma viene eseguita con il paziente che trattiene il respiro in due direzioni: rispetto agli assi longitudinale e trasversale del dispositivo ricevente. Il confronto di vari dinamocardiogrammi è mostrato in fico. 1.12.

Sismocardiografia si basa sulla registrazione delle vibrazioni meccaniche del corpo umano causate dal lavoro del cuore. In questo metodo, utilizzando sensori installati nella regione della base del processo xifoideo, viene registrato un impulso cardiaco dovuto all'attività meccanica del cuore durante il periodo di contrazione. In questo caso, ci sono processi associati all'attività dei meccanocettori tissutali del letto vascolare, che si attivano quando il volume del sangue circolante diminuisce. Il sismocardiosignal forma la forma delle oscillazioni dello sterno.

Riso. 1.12. Registrazione di normali dinamocardiogrammi longitudinali (a) e trasversali (b).

Vibrazione

L'introduzione diffusa di varie macchine e meccanismi nella vita umana aumenta la produttività del lavoro. Tuttavia, il lavoro di molti meccanismi è associato al verificarsi di vibrazioni che vengono trasmesse a una persona e hanno un effetto dannoso su di lui.

Vibrazione- oscillazioni forzate del corpo, in cui o l'intero corpo oscilla nel suo insieme o le sue parti separate oscillano con ampiezze e frequenze diverse.

Una persona sperimenta costantemente vari tipi di effetti vibrazionali nei trasporti, al lavoro, a casa. Le vibrazioni che si sono verificate in qualsiasi punto del corpo (ad esempio la mano di un operaio che impugna un martello pneumatico) si propagano in tutto il corpo sotto forma di onde elastiche. Queste onde provocano deformazioni variabili di vario tipo nei tessuti del corpo (compressione, tensione, taglio, flessione). L'effetto delle vibrazioni su una persona è dovuto a molti fattori che caratterizzano le vibrazioni: frequenza (spettro di frequenza, frequenza fondamentale), ampiezza, velocità e accelerazione di un punto oscillante, energia dei processi oscillatori.

L'esposizione prolungata alle vibrazioni provoca disturbi persistenti nelle normali funzioni fisiologiche del corpo. Potrebbe verificarsi "malattia da vibrazione". Questa malattia porta a una serie di gravi disturbi nel corpo umano.

L'influenza che le vibrazioni hanno sul corpo dipende dall'intensità, dalla frequenza, dalla durata delle vibrazioni, dal luogo della loro applicazione e dalla direzione in relazione al corpo, alla postura, nonché dallo stato della persona e dalle sue caratteristiche individuali.

Le fluttuazioni con una frequenza di 3-5 Hz causano reazioni dell'apparato vestibolare, disturbi vascolari. A frequenze di 3-15 Hz si osservano disturbi associati alle vibrazioni risonanti dei singoli organi (fegato, stomaco, testa) e del corpo nel suo insieme. Le fluttuazioni con frequenze di 11-45 Hz causano visione offuscata, nausea e vomito. A frequenze superiori a 45 Hz si verificano danni ai vasi cerebrali, ridotta circolazione sanguigna, ecc. La Figura 1.13 mostra gli intervalli di frequenza delle vibrazioni che hanno un effetto dannoso su una persona e sui suoi sistemi di organi.

Riso. 1.13. Le gamme di frequenza degli effetti nocivi delle vibrazioni sull'uomo

Allo stesso tempo, in alcuni casi, le vibrazioni vengono utilizzate in medicina. Ad esempio, utilizzando un vibratore speciale, il dentista prepara un amalgama. L'uso di dispositivi di vibrazione ad alta frequenza consente di praticare un foro di forma complessa nel dente.

La vibrazione è usata anche nel massaggio. Con il massaggio manuale, i tessuti massaggiati vengono portati in movimento oscillatorio con l'aiuto delle mani del massaggiatore. Con il massaggio hardware vengono utilizzati vibratori, in cui vengono utilizzate punte di varie forme per trasmettere movimenti oscillatori al corpo. I dispositivi vibranti sono suddivisi in dispositivi per la vibrazione generale, che provocano lo scuotimento di tutto il corpo (vibrante "sedia", "letto", "piattaforma", ecc.) E dispositivi per l'impatto delle vibrazioni locali su singole parti del corpo.

Meccanoterapia

Negli esercizi di fisioterapia (LFK) vengono utilizzati simulatori, sui quali vengono eseguiti movimenti oscillatori di varie parti del corpo umano. Sono usati in meccanoterapia - forma di terapia fisica, uno dei cui compiti è l'esecuzione di esercizi fisici dosati e ripetuti ritmicamente allo scopo di allenare o ripristinare la mobilità delle articolazioni su dispositivi a pendolo. La base di questi dispositivi è l'equilibrio (da fr. bilanciatore- swing, balance) un pendolo, che è una leva a due bracci che esegue movimenti oscillatori (a dondolo) attorno ad un asse fisso.

1.7. Concetti base e formule

Continuazione della tabella

Continuazione della tabella

Fine del tavolo

1.8. Compiti

1. Fornisci esempi di sistemi oscillatori nell'uomo.

2. In un adulto, il cuore fa 70 contrazioni al minuto. Determinare: a) la frequenza delle contrazioni; b) il numero di tagli in 50 anni

Risposta: a) 1,17 Hz; b) 1,84x10 9 .

3. Quale lunghezza deve avere un pendolo matematico affinché il suo periodo di oscillazione sia pari a 1 secondo?

4. Una sottile asta dritta omogenea lunga 1 m è sospesa per la sua estremità su un asse. Determina: a) qual è il periodo delle sue oscillazioni (piccole)? b) qual è la lunghezza di un pendolo matematico con lo stesso periodo di oscillazione?

5. Un corpo con una massa di 1 kg oscilla secondo la legge x = 0,42 cos (7,40 t), dove t si misura in secondi e x si misura in metri. Trova: a) ampiezza; b) frequenza; c) energia totale; d) energie cinetiche e potenziali a x = 0.16 m.

6. Stimare la velocità con cui una persona cammina con una lunghezza del passo l= 0,65 m Lunghezza gamba L = 0,8 m; il baricentro si trova ad una distanza H = 0,5 m dal piede. Per il momento d'inerzia della gamba rispetto all'articolazione dell'anca, utilizzare la formula I = 0,2 ml 2 .

7. Come puoi determinare la massa di un piccolo corpo a bordo di una stazione spaziale se hai a disposizione un orologio, una molla e una serie di pesi?

8. L'ampiezza delle oscillazioni smorzate diminuisce in 10 oscillazioni di 1/10 del suo valore originale. Periodo di oscillazione T = 0,4 s. Determinare il decremento logaritmico e il fattore di smorzamento.

VIBRAZIONI MECCANICHE

Consideriamo le oscillazioni eseguite nei sistemi meccanici.

Le oscillazioni sono processi che hanno un certo grado di ripetizione nel tempo.

Sono gratuito, se vengono eseguiti a scapito dell'energia inizialmente comunicata con la conseguente assenza di influenze esterne sul sistema oscillatorio. Le vibrazioni libere possono essere non smorzato e sbiadito.

Un altro tipo di oscillazione - costretto, vengono eseguiti sotto l'azione di una forza esterna che agisce periodicamente.

Il tipo più semplice di vibrazioni sono armonico. Sia le vibrazioni libere che quelle forzate possono essere armoniche.

Vibrazioni libere non smorzate

La fluttuazione a cui il valore X il valore fluttuante cambia nel tempo T legalmente

x=A peccato(ω 0 T+a 0) o

x=A cos(ω 0 t+ a), (1.1)

chiamato armonico.

Nelle espressioni (1.1) per le vibrazioni meccaniche X- spostamento del punto oscillante dalla posizione di equilibrio; UN- ampiezza di oscillazione (spostamento massimo); (ω0 t+a) - la fase delle oscillazioni al momento del tempo T; a, a 0 - fasi iniziali al tempo t = 0; ω 0 - propria frequenza ciclica. Un confronto delle equazioni mostra che le fasi iniziali sono correlate: a = a 0 - p / 2. In SI, la fase è misurata in radianti(per comodità n azioni p, ad esempio p/2), ma può anche essere misurato in gradi.

Le oscillazioni armoniche meccaniche vengono eseguite sotto l'azione di elastico O quasi elastico forza proporzionale allo spostamento e sempre diretta verso la posizione di equilibrio, cioè obbediente alla legge F = -kx, Dove K- coefficiente di proporzionalità (per la forza elastica, il coefficiente di rigidezza).

Poiché - 1 ≤ сos(ω 0 T+a) ≤ 1 e - 1 ≤ sin(ω 0 T+a 0) ≤ 1, quindi il valore X varia da - UN a + UN.

Viene chiamato il numero di oscillazioni complete per unità di tempo frequenza nm, e il tempo di un'oscillazione completa è periodo di oscillazione T. Il periodo della funzione armonica è correlato alla frequenza ciclica:

T= 2p / ω 0 . (1.2)

La frequenza è inversamente proporzionale al periodo, quindi

N = 1/T,ω 0 = 2pn . (1.3)

L'unità di frequenza è hertz(Hz). 1 Hz è la frequenza di oscillazione alla quale avviene un'oscillazione completa in un secondo, 1 Hz = 1 s -1.

La frequenza ciclica è pari al numero di oscillazioni complete in 2p secondi, misurate in s -1 .

Periodo di oscillazione T può essere determinato dai grafici (Fig. 1.1).

Coseno e seno sono funzioni periodiche, quindi si ripetono per il valore dell'argomento pari a 2 π radianti, cioè dopo un periodo di oscillazione, la fase passa a 2π radiante. Funzione X= peccato( T) parte da zero, in Fig. 1.1 UN il suo inizio è Sinistra fuori asse Bue, il grafico viene spostato nel tempo di T/ 8, e in fase di π / 4 rad. Per tornare all'inizio del grafico, devi spostarti Di asse del tempo, quindi la fase è presa con un segno più: α 0 = π/4 rad.

Conto alla rovescia fase iniziale secondo la legge del coseno (Fig. 1.1, B) è fatto dalla “gobba” del grafico, poiché la funzione X= cos( T) è uguale a uno a T= 0. Il grafico viene spostato in modo che il valore del coseno massimo più vicino si trovi a destra dell'asse Bue: di volta in volta T/ 8, e in fase di π / 4 rad. Il ritorno all'origine degli assi coordinati avviene opposto all'asse dei tempi, la fase iniziale in questo caso è considerata con segno meno: α = - π/4 rad. Fase istantanea oscillazioni determina lo stato del sistema oscillatorio in un dato momento. Per punto M(figura 1.1, B) nell'equazione, secondo la legge del seno, la fase delle oscillazioni è uguale a π radianti, perché dal valore della funzione più vicino X= peccato( T) A T= 0 è trascorsa metà del periodo prima del momento specificato. È trascorso un quarto del periodo dalla "gobba" più vicina, quindi, secondo la legge del coseno, la fase è π / 2 radianti.

Ti ricordiamo che queste funzioni sono periodiche, quindi puoi aggiungere (o sottrarre) un numero pari π alla fase - questo non cambierà lo stato del sistema oscillatorio.