अभी आप यहाँ हो? =) नहीं, मैंने किसी को डराने की कोशिश नहीं की, यह सिर्फ इतना है कि अनुचित इंटीग्रल्स का विषय इस बात का बहुत अच्छा उदाहरण है कि उच्च गणित और अन्य सटीक विज्ञानों को चलाना कितना महत्वपूर्ण है। साइट पर पाठ में महारत हासिल करने के लिए, सब कुछ है - एक विस्तृत और सुलभ रूप में, एक इच्छा होगी ....

चलिए, शुरू करते हैं। लाक्षणिक रूप से बोलना, एक अनुचित अभिन्न एक "उन्नत" निश्चित अभिन्न है, और वास्तव में उनके साथ इतनी कठिनाइयाँ नहीं हैं, इसके अलावा, एक अनुचित अभिन्न का एक बहुत अच्छा ज्यामितीय अर्थ है।

अनुचित समाकलन की गणना करने का क्या अर्थ है?

अनुचित इंटीग्रल की गणना करें - इसका मतलब NUMBER . खोजना है(बिल्कुल निश्चित अभिन्न के समान), या साबित करें कि यह अलग हो जाता है(अर्थात, एक संख्या के बजाय अनंत के साथ समाप्त होता है)।

अनुचित समाकलन दो प्रकार के होते हैं।

एकीकरण की अनंत सीमा (ओं) के साथ अनुचित समाकलन

कभी-कभी ऐसे अनुचित समाकलन को कहा जाता है पहली तरह का अनुचित अभिन्न अंग. सामान्य तौर पर, एक अनंत सीमा के साथ एक अनुचित अभिन्न अक्सर इस तरह दिखता है: . यह एक निश्चित समाकल से किस प्रकार भिन्न है? ऊपरी सीमा में। यह अंतहीन है:

कम आम एक अनंत निचली सीमा के साथ या दो अनंत सीमाओं के साथ इंटीग्रल हैं: , और हम बाद में उन पर विचार करेंगे - जब आपको स्वाद मिलेगा :)

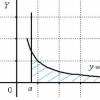
खैर, अब सबसे लोकप्रिय मामले का विश्लेषण करते हैं। अधिकांश उदाहरणों में, एकीकृत कार्य निरंतरबीच में और यह एक पहले जाँच करने के लिए महत्वपूर्ण तथ्य!यदि अंतराल हैं, तो अतिरिक्त बारीकियां हैं। निश्चितता के लिए, हम मानते हैं कि तब भी विशिष्ट वक्रीय समलम्ब चतुर्भुजइस तरह दिखेगा:

ध्यान दें कि यह अनंत है (दाईं ओर सीमित नहीं है), और अभिन्न अनुचितसंख्यात्मक रूप से अपने क्षेत्र के बराबर. इस मामले में, निम्नलिखित विकल्प संभव हैं:

1) पहला विचार जो दिमाग में आता है वह है: "चूंकि आकृति अनंत है, तो ”, दूसरे शब्दों में, क्षेत्रफल भी अनंत है। तो हो सकता है।इस मामले में, हम कहते हैं कि अनुचित अभिन्न अलग करना.

2) परंतु. जैसा कि यह विरोधाभासी लग सकता है, एक अनंत आकृति का क्षेत्रफल बराबर हो सकता है ... एक परिमित संख्या! उदाहरण के लिए: । यह हो सकता है? आसान। दूसरे मामले में, अनुचित अभिन्न अभिसरण.

3) तीसरे विकल्प के बारे में थोड़ी देर बाद।

एक अनुचित अभिन्न विचलन कब होता है और कब अभिसरण होता है? यह एकीकृत पर निर्भर करता है, और हम बहुत जल्द ठोस उदाहरण देखेंगे।

लेकिन क्या होता है यदि एक अनंत वक्रीय समलम्ब चतुर्भुज अक्ष के नीचे स्थित होता है? इस मामले में, अनुचित अभिन्न (विचलन) या एक परिमित ऋणात्मक संख्या के बराबर है।

इस तरह, अनुचित अभिन्न नकारात्मक हो सकता है.

महत्वपूर्ण!जब कोई अनुचित समाकलन आपको हल करने के लिए पेश किया जाता है, तो सामान्यतया, किसी क्षेत्र की बात नहीं है और न ही कोई चित्र बनाने की आवश्यकता है. मैंने सामग्री को समझने में आसान बनाने के लिए केवल अनुचित अभिन्न का ज्यामितीय अर्थ बताया।

चूँकि अनुचित समाकल निश्चित समाकल से बहुत मिलता-जुलता है, इसलिए हमें न्यूटन-लीबनिज़ सूत्र याद आता है: . वास्तव में, सूत्र अनुचित समाकलों पर भी लागू होता है, केवल इसे थोड़ा संशोधित करने की आवश्यकता होती है। क्या फर्क पड़ता है? एकीकरण की अनंत ऊपरी सीमा में: . शायद, कई लोगों ने अनुमान लगाया है कि यह पहले से ही सीमा के सिद्धांत को लागू करने की बू आ रही है, और सूत्र इस प्रकार लिखा जाएगा: .

यह एक निश्चित समाकल से किस प्रकार भिन्न है? हाँ, कुछ खास नहीं! एक निश्चित समाकल के रूप में, आपको प्रतिअवकलन फलन (अनिश्चित समाकलन) खोजने में सक्षम होने की आवश्यकता है, न्यूटन-लीबनिज़ सूत्र को लागू करने में सक्षम होना चाहिए। केवल एक चीज जो जोड़ी गई है वह है सीमा की गणना। उनके साथ कौन बुरा है, सबक सीखो कार्यों की सीमा। समाधान उदाहरणक्योंकि सेना में देर से आने से अच्छा है।

दो क्लासिक उदाहरणों पर विचार करें:

उदाहरण 1

स्पष्टता के लिए, मैं एक चित्र बनाऊंगा, हालांकि, मैं एक बार फिर जोर देता हूं, अभ्यास पर इस कार्य में चित्र बनाना आवश्यक नहीं है.

इंटीग्रैंड आधे अंतराल पर निरंतर है, जिसका अर्थ है कि सब कुछ ठीक है और अनुचित अभिन्न की गणना "नियमित" विधि का उपयोग करके की जा सकती है।

हमारे सूत्र का अनुप्रयोग और समाधान इस तरह दिखता है:

यही है, अनुचित अभिन्न विचलन, और छायांकित वक्रतापूर्ण ट्रेपोजॉइड का क्षेत्र अनंत के बराबर है।

विचार किए गए उदाहरण में, हमारे पास सबसे सरल सारणीबद्ध समाकलन है और न्यूटन-लीबनिज़ सूत्र को लागू करने की वही तकनीक है जो निश्चित समाकलन में है। लेकिन यह सूत्र सीमा के संकेत के तहत लागू होता है। "डायनेमिक" वेरिएबल के सामान्य अक्षर के बजाय, "बी" अक्षर दिखाई देता है। यह भ्रमित या भ्रमित नहीं होना चाहिए, क्योंकि कोई भी अक्षर मानक "X" से भी बदतर नहीं है।

यदि आपको समझ में नहीं आता है कि क्यों कब , तो यह बहुत बुरा है, या तो आप सरलतम सीमाओं को नहीं समझते हैं (और यह नहीं समझते कि सीमा क्या है), या आप नहीं जानते कि लघुगणक का ग्राफ क्या है समारोह की तरह दिखता है। दूसरे मामले में, पाठ पर जाएँ प्राथमिक कार्यों के रेखांकन और गुण.

अनुचित इंटीग्रल को हल करते समय, यह जानना बहुत महत्वपूर्ण है कि मुख्य प्राथमिक कार्यों के ग्राफ़ कैसे दिखते हैं!

एक साफ नौकरी डिजाइन कुछ इस तरह दिखना चाहिए:

“

! एक उदाहरण तैयार करते समय, हम हमेशा समाधान को बाधित करते हैं और इंगित करते हैं कि एकीकृत का क्या होता है – क्या यह एकीकरण के अंतराल पर निरंतर है या नहीं. इसके द्वारा हम अनुचित अभिन्न के प्रकार की पहचान करते हैं और आगे की कार्रवाइयों को प्रमाणित करते हैं।

उदाहरण 2

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

आइए एक चित्र बनाएं:

सबसे पहले, हम निम्नलिखित नोटिस करते हैं: आधा अंतराल पर इंटीग्रैंड निरंतर है। अच्छा। सूत्र द्वारा हल करना :

(1) हम एक शक्ति फ़ंक्शन का सबसे सरल अभिन्न अंग लेते हैं (यह विशेष मामला कई तालिकाओं में है)। माइनस को तुरंत सीमा चिन्ह से आगे ले जाना बेहतर है ताकि आगे की गणना में यह नीचे न आ जाए।

(2) हम न्यूटन-लीबनिज सूत्र के अनुसार ऊपरी और निचली सीमाओं को प्रतिस्थापित करते हैं।

(3) हम इंगित करते हैं कि जब (सज्जनों, यह लंबे समय से समझा गया है) और उत्तर को सरल बनाएं।

यहाँ, एक अनंत वक्रीय समलंब चतुर्भुज का क्षेत्रफल एक परिमित संख्या के बराबर है! अविश्वसनीय, लेकिन यह एक सच्चाई है।

उदाहरण का साफ डिजाइन कुछ इस तरह दिखना चाहिए:

“

इंटीग्रैंड निरंतर चालू है

“

यदि आप एक अभिन्न जैसे - के साथ आते हैं तो क्या करें अत्यंत तनावग्रस्त स्थितिएकीकरण के अंतराल पर? इसका मतलब है कि उदाहरण में एक टाइपो है (सबसे अधिक संभावना)या शिक्षा का एक उन्नत स्तर। बाद के मामले में, के कारण योजक गुण, किसी को अंतराल पर दो अनुचित समाकलों पर विचार करना चाहिए और फिर योग के साथ व्यवहार करना चाहिए।

कभी-कभी, टाइपो या अनुचित अभिन्न के इरादे के कारण, यह हो सकता है बिल्कुल मौजूद नहीं है, इसलिए, उदाहरण के लिए, यदि "x" का वर्गमूल उपरोक्त समाकलन के हर में रखा जाता है, तो एकीकरण अंतराल का भाग समाकलन की परिभाषा के क्षेत्र में बिल्कुल भी प्रवेश नहीं करेगा।

इसके अलावा, एक अनुचित अभिन्न सभी "स्पष्ट भलाई" के साथ भी मौजूद नहीं हो सकता है। क्लासिक उदाहरण: . कोसाइन की निश्चितता और निरंतरता के बावजूद, ऐसा अनुचित समाकलन मौजूद नहीं है! क्यों? यह बहुत आसान है क्योंकि:
- मौजूद नहीं संगत सीमा.

और ऐसे उदाहरण, हालांकि दुर्लभ हैं, व्यवहार में पाए जाते हैं! इस प्रकार, अभिसरण और विचलन के अलावा, एक पूर्ण उत्तर के साथ समाधान का तीसरा परिणाम भी है: "कोई अनुचित अभिन्न नहीं है।"

यह भी ध्यान दिया जाना चाहिए कि अनुचित अभिन्न की सख्त परिभाषा सीमा के माध्यम से सटीक रूप से दी गई है, और जो चाहें शैक्षिक साहित्य में खुद को इससे परिचित कर सकते हैं। खैर, हम व्यावहारिक पाठ जारी रखते हैं और अधिक सार्थक कार्यों की ओर बढ़ते हैं:

उदाहरण 3

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

सबसे पहले, आइए एंटीडेरिवेटिव फ़ंक्शन (अनिश्चित अभिन्न) को खोजने का प्रयास करें। यदि हम ऐसा करने में विफल रहते हैं, तो स्वाभाविक रूप से हम अनुचित समाकलन को भी हल नहीं करेंगे।

कौन सा टेबल इंटीग्रल इंटीग्रैंड जैसा दिखता है? यह मुझे चाप स्पर्शरेखा की याद दिलाता है: . इन विचारों से, विचार स्वयं ही बताता है कि हर में एक वर्ग प्राप्त करना अच्छा होगा। यह प्रतिस्थापन द्वारा किया जाता है।

आइए प्रतिस्थापित करें:

अनिश्चित अभिन्न पाया गया है, इस मामले में एक स्थिरांक जोड़ने का कोई मतलब नहीं है।

मसौदे पर, जाँच करना हमेशा उपयोगी होता है, अर्थात परिणाम में अंतर करना:

मूल समाकलन प्राप्त हुआ, जिसका अर्थ है कि अनिश्चित समाकलन सही पाया गया।

अब हम अनुचित अभिन्न पाते हैं:

(1) हम सूत्र के अनुसार हल लिखते हैं . यह बेहतर है कि स्थिरांक को तुरंत सीमा चिन्ह से आगे ले जाया जाए ताकि यह आगे की गणना में हस्तक्षेप न करे।

(2) हम न्यूटन-लीबनिज सूत्र के अनुसार ऊपरी और निचली सीमाओं को प्रतिस्थापित करते हैं। क्यों पर ? पहले से बार-बार अनुशंसित आलेख में चाप स्पर्शरेखा ग्राफ़ देखें।

(3) हमें अंतिम उत्तर मिलता है। तथ्य यह है कि यह दिल से जानना उपयोगी है।

उन्नत छात्रों को अनिश्चितकालीन अभिन्न अलग से नहीं मिल सकता है, और प्रतिस्थापन विधि का उपयोग नहीं कर सकते हैं, लेकिन अंतर चिह्न के तहत फ़ंक्शन को सारांशित करने की विधि का उपयोग करें और अनुचित अभिन्न को "तुरंत" हल करें। इस मामले में, समाधान कुछ इस तरह दिखना चाहिए:

“

इंटीग्रैंड चालू है।

“

उदाहरण 4

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

! यह एक विशिष्ट उदाहरण है, और समान समाकलन बहुत सामान्य हैं। इसे अच्छी तरह से काम करें! एक पूर्ण वर्ग का चयन करने की विधि द्वारा यहां एंटीडेरिवेटिव फ़ंक्शन पाया जाता है, विधि के बारे में अधिक विवरण पाठ में पाया जा सकता है कुछ भिन्नों का एकीकरण.

उदाहरण 5

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

इस समाकल को विस्तार से हल किया जा सकता है, अर्थात् पहले चर को बदलकर अनिश्चितकालीन समाकल ज्ञात कीजिए। और आप इसे "तुरंत" हल कर सकते हैं - अंतर के संकेत के तहत फ़ंक्शन को सारांशित करके। जिसकी कुछ गणितीय पृष्ठभूमि हो।

पाठ के अंत में पूर्ण समाधान और उत्तर।

एकीकरण की अनंत निचली सीमा के साथ अनुचित समाकलन के समाधान के उदाहरण पृष्ठ पर पाए जा सकते हैं अनुपयुक्त समाकलनों को हल करने की दक्ष विधियाँ. वह मामला जहां दोनों एकीकरण सीमाएं अनंत हैं, वहां भी विचार किया जाता है।

असीमित कार्यों के अनुचित समाकलन

या दूसरे प्रकार के अनुचित समाकलन. दूसरे प्रकार के अनुचित समाकल सामान्य निश्चित समाकल के अंतर्गत कपटपूर्ण रूप से "एन्क्रिप्टेड" होते हैं और बिल्कुल एक जैसे दिखते हैं: लेकिन, निश्चित समाकल के विपरीत, समाकलन एक अनंत असंततता (अस्तित्व में नहीं है): 1) बिंदु पर, 2) या बिंदु पर , 3) ​​या दोनों बिंदुओं पर एक साथ, 4) या एकीकरण के अंतराल पर भी। हम पहले दो मामलों पर विचार करेंगे, लेख के अंत में 3-4 मामलों के लिए एक अतिरिक्त पाठ का लिंक है।

इसे स्पष्ट करने के लिए सिर्फ एक उदाहरण:। यह एक निश्चित अभिन्न प्रतीत होता है। लेकिन वास्तव में, यह दूसरी तरह का एक अनुचित अभिन्न अंग है, यदि हम निचली सीमा के मूल्य को समाकलन में प्रतिस्थापित करते हैं, तो भाजक गायब हो जाता है, अर्थात इस बिंदु पर समाकलन मौजूद नहीं है!

सामान्य तौर पर, अनुचित अभिन्न का विश्लेषण करते समय दोनों एकीकरण सीमाओं को एकीकृत में प्रतिस्थापित करना हमेशा आवश्यक होता है. इस संबंध में, हम ऊपरी सीमा की भी जाँच करते हैं: . यहां सब कुछ अच्छा है।

अनुचित अभिन्न की मानी गई विविधता के लिए वक्रतापूर्ण समलम्ब मूल रूप से इस तरह दिखता है:

यहाँ, लगभग सब कुछ पहले प्रकार के समाकलन जैसा ही है।

हमारा अभिन्न संख्यात्मक रूप से छायांकित वक्रीय समलम्बाकार क्षेत्र के बराबर है, जो ऊपर से घिरा नहीं है। इस मामले में, दो विकल्प हो सकते हैं *: अनुचित अभिन्न विचलन (क्षेत्र अनंत है) या अनुचित अभिन्न एक परिमित संख्या के बराबर है (अर्थात, एक अनंत आकृति का क्षेत्र परिमित है!)।

* डिफ़ॉल्ट रूप से, हम आदतन यह मान लेते हैं कि अनुचित समाकल मौजूद है

यह केवल न्यूटन-लीबनिज सूत्र को संशोधित करने के लिए बनी हुई है। इसे सीमा की सहायता से संशोधित भी किया जाता है, लेकिन सीमा अब अनंत तक नहीं जाती है, लेकिन मूल्य के लिए दाईं ओर।ड्राइंग के साथ पालन करना आसान है: अक्ष के साथ, हमें ब्रेकिंग पॉइंट के असीम रूप से करीब पहुंचना चाहिए दायी ओर.

आइए देखें कि इसे व्यवहार में कैसे लागू किया जाता है।

उदाहरण 6

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

इंटीग्रैंड को एक बिंदु पर एक अनंत विराम का सामना करना पड़ता है (यदि ऊपरी सीमा के साथ सब कुछ ठीक है तो मौखिक रूप से या मसौदे की जांच करना न भूलें!)

सबसे पहले, हम अनिश्चितकालीन अभिन्न की गणना करते हैं:

प्रतिस्थापन:

जिन लोगों को प्रतिस्थापन में कठिनाई होती है, उनके लिए पाठ देखें अनिश्चितकालीन समाकलन में प्रतिस्थापन विधि.

हम अनुचित अभिन्न की गणना करते हैं:

(1) यहाँ नया क्या है? तकनीक के मामले में व्यावहारिक रूप से कुछ भी नहीं। केवल एक चीज जो बदली है वह है लिमिट आइकन के तहत एंट्री: . जोड़ का अर्थ है कि हम दाईं ओर के मान को लक्षित कर रहे हैं (जो तार्किक है - ग्राफ़ देखें)। सीमा के सिद्धांत में ऐसी सीमा कहलाती है एकतरफा सीमा. इस मामले में हमारे पास है दाहिने हाथ की सीमा.

(2) हम न्यूटन-लीबनिज सूत्र के अनुसार ऊपरी और निचली सीमाओं को प्रतिस्थापित करते हैं।

(3) से निपटने के लिए . आप कैसे निर्धारित करते हैं कि एक अभिव्यक्ति कहाँ जा रही है? मोटे तौर पर, आपको बस इसमें मूल्य को स्थानापन्न करने की आवश्यकता है, तीन चौथाई स्थानापन्न करें और इंगित करें कि . उत्तर मिलाना।

इस मामले में, अनुचित अभिन्न एक ऋणात्मक संख्या के बराबर है। इसमें कोई अपराध नहीं है, बस संबंधित वक्रताकार ट्रेपोजॉइड अक्ष के नीचे स्थित है।

और अब एक स्वतंत्र निर्णय के लिए दो उदाहरण।

उदाहरण 7

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

उदाहरण 8

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

यदि बिंदु पर समाकलन मौजूद नहीं है

इस तरह के एक अनुचित अभिन्न के लिए एक अनंत वक्रीय समलम्ब मूल रूप से इस तरह दिखता है।

कभी-कभी ऐसे अनुचित समाकलन कहलाते हैं दूसरे प्रकार के अनुचित समाकलन. दूसरे प्रकार के अनुचित समाकलन सामान्य निश्चित समाकलन के अंतर्गत चालाकी से "एन्क्रिप्टेड" होते हैं और बिल्कुल एक जैसे दिखते हैं: .

लेकिन, निश्चित इंटीग्रल के विपरीत, इंटीग्रैंड एक अनंत असंततता से ग्रस्त है (अस्तित्व में नहीं है):

1) बिंदु पर,

2) बिंदु,

3) दोनों बिंदुओं पर एक साथ,

4) या एकीकरण के अंतराल पर भी।

हम पहले दो मामलों पर विचार करेंगे, लेख के अंत में 3-4 मामलों के लिए एक अतिरिक्त पाठ का लिंक है।

आइए इसे स्पष्ट करने के लिए एक उदाहरण देखें:

यह एक निश्चित अभिन्न प्रतीत होता है। लेकिन वास्तव में, यह दूसरी तरह का एक अनुचित अभिन्न अंग है, क्योंकि यदि हम समाकलन में स्थानापन्न करते हैं, तो निचली सीमा का मान

तब भाजक गायब हो जाता है, अर्थात, इस बिंदु पर एकीकृत बस मौजूद नहीं है!

अनुचित अभिन्न का विश्लेषण करते समय दोनों एकीकरण सीमाओं को एकीकृत में प्रतिस्थापित करना हमेशा आवश्यक होता है. इस संबंध में, हम ऊपरी सीमा की भी जाँच करते हैं:

यहां सब कुछ अच्छा है। अनुचित अभिन्न की मानी गई विविधता के लिए वक्रतापूर्ण समलम्ब मूल रूप से इस तरह दिखता है:

यहाँ, लगभग सब कुछ पहले प्रकार के समाकलन जैसा ही है। हमारा अभिन्न संख्यात्मक रूप से छायांकित वक्रीय समलम्बाकार क्षेत्र के बराबर है, जो ऊपर से घिरा नहीं है। इस मामले में, दो विकल्प हो सकते हैं: अनुचित अभिन्न विचलन (क्षेत्र अनंत है), या अनुचित अभिन्न एक सीमित संख्या के बराबर है (जब एक अनंत आकृति का क्षेत्र सीमित है!)।

यह केवल न्यूटन-लीबनिज सूत्र को संशोधित करने के लिए बनी हुई है। इसे सीमा की सहायता से संशोधित भी किया जाता है, लेकिन सीमा अब अनंत तक नहीं जाती है, लेकिन मान के लिए दायी ओर।ड्राइंग का पालन करना आसान है, जो अक्ष के साथ है बैल दायी ओर.

आइए देखें कि इसे व्यवहार में कैसे लागू किया जाता है।

उदाहरण 6

(यदि ऊपरी सीमा के साथ सब कुछ ठीक है तो मौखिक रूप से या मसौदे पर जांचना न भूलें!) सबसे पहले, हम अनिश्चितकालीन अभिन्न की गणना करते हैं:

जिन लोगों को प्रतिस्थापन में कठिनाई होती है, उनके लिए पाठ देखें अनिश्चितकालीन समाकलन में प्रतिस्थापन विधि.

हम अनुचित अभिन्न की गणना करते हैं:

(1) यहाँ नया क्या है? तकनीक के मामले में व्यावहारिक रूप से कुछ भी नहीं। केवल एक चीज जो बदल गई है वह है लिमिट आइकन के तहत एंट्री:

+0 जोड़ने का अर्थ है कि हम दाईं ओर के मान को लक्षित कर रहे हैं, जो तार्किक है (ग्राफ देखें)। सीमा के सिद्धांत में ऐसी सीमा कहलाती है एकतरफा सीमा. इस मामले में हमारे पास है दाहिने हाथ की सीमा.

(2) हम न्यूटन-लीबनिज सूत्र के अनुसार ऊपरी और निचली सीमाओं को प्रतिस्थापित करते हैं।

(3) से निपटने के लिए . आप कैसे निर्धारित करते हैं कि एक अभिव्यक्ति कहाँ जा रही है? मोटे तौर पर, आपको बस इसमें मूल्य को स्थानापन्न करने की आवश्यकता है, तीन चौथाई स्थानापन्न करें और इंगित करें कि . उत्तर मिलाना।

इस मामले में, अनुचित अभिन्न एक ऋणात्मक संख्या के बराबर है। इसमें कोई अपराध नहीं है, बस इसी वक्रीय समलम्बाकार अक्ष के नीचे स्थित है बैल. और अब स्वतंत्र निर्णय के लिए उदाहरण।

उदाहरण 7

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

उदाहरण 8

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

यदि बिंदु पर समाकलन मौजूद नहीं है

इस तरह के एक अनुचित अभिन्न के लिए एक अनंत वक्रीय समलम्ब मूल रूप से इस तरह दिखता है:

यहां हम पूरी तरह से सब कुछ वही करते हैं, सिवाय इसके कि सीमा की ओर जाता है मान के लिए बीबाएं।एक्सिस बैलहमें असीम रूप से ब्रेकिंग पॉइंट के करीब पहुंचना चाहिए बाएं.

उदाहरण 9

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

इंटीग्रैंड को एक बिंदु पर अनंत असंततता का सामना करना पड़ता है बी = 3 (हम मौखिक रूप से जांचते हैं कि एक अलग एकीकरण सीमा के साथ सब कुछ ठीक है!)

एक बदलाव के लिए, हम इस सीमा को तुरंत हल करेंगे - फ़ंक्शन को अंतर के संकेत के तहत लाकर। जिन लोगों को यह मुश्किल लगता है, वे पहले से ही पहले से मानी गई योजना के अनुसार अनिश्चितकालीन अभिन्न पा सकते हैं।

जोड़ (-0) का मतलब है कि हमारे पास एक सीमा है बाएँ तरफा, और बिंदु तक बी = 3 हम धुरी के करीब आ रहे हैं बैल बाएं.

हम समझते हैं कि भिन्न क्यों

(यह मौखिक रूप से या मसौदे के रूप में सबसे अच्छा किया जाता है)।

हम रूट के तहत सीमा मान को प्रतिस्थापित करते हैं बी = 3 - 0.

आखिरकार:

अनुचित अभिन्न विचलन।

माइनस साइन का मतलब है कि संबंधित वक्रीय समलम्बाकार अक्ष के नीचे स्थित है बैल. संकेतों से बहुत सावधान रहें।

हां, निश्चित रूप से, अनुचित अभिन्न विचलन, लेकिन वे अलग-अलग चीजें हैं, अलग-अलग शैलियां हैं, और यदि आप संकेतों की अनदेखी करते हैं, तो, कड़ाई से बोलते हुए, एक गंभीर गलती करें।

और आत्मचिंतन के लिए अंतिम दो उदाहरण:

उदाहरण 10

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

उदाहरण 11

अनुचित समाकल की गणना कीजिए या इसका विचलन स्थापित कीजिए।

उस स्थिति का विश्लेषण जब दोनों एकीकरण सीमाएं "खराब" हैं, या विघटन बिंदु सीधे एकीकरण खंड पर निहित है, लेख में पाया जा सकता है निश्चित और अनुचित समाकलों को हल करने की दक्ष विधियाँ.

समाधान और उत्तर:

उदाहरण 4: हल:

.

उदाहरण 5: हल:

इंटीग्रैंड निरंतर चालू है .

उदाहरण 7: हल:

इंटीग्रैंड को एक बिंदु पर अनंत असंततता का सामना करना पड़ता है

अनुचित अभिन्न विचलन।

नोट: अभिव्यक्ति सीमा के साथ

2पहली तरह के अनुचित समाकलनरूप के समाकलन कहलाते हैं समाकलन को संपूर्ण समाकलन खंड पर निरंतर माना जाता है।

2 यदि सीमा मौजूद है और परिमित है, तो अनुचित अभिन्न को अभिसरण और बराबर होना कहा जाता है

इंटीग्रल और समान रूप से परिभाषित किए गए हैं:

(8.21)
कहाँ पे एककोई वास्तविक संख्या है। इसके अलावा, अंतिम समाकलन को अभिसरण करने के लिए कहा जाता है यदि और केवल यदि इसके अभिन्न अंग के दोनों घटक अभिसरण करते हैं।

समस्या 8.10.

समाधान।

इसलिए, अभिन्न विचलन।

समस्या 8.11।अनुचित अभिन्न की गणना करें।

समाधान।

यह अभिन्न अभिसरण करता है।

2 दूसरे प्रकार के अनुचित समाकलनप्रपत्र के समाकलन कहलाते हैं: , जहाँ समाकलन एफ(एक्स) परिमित अंतराल पर अनंत असंततता है [ एक; बी]. अंतराल पर असंततता बिंदुओं के स्थान के आधार पर, दूसरे प्रकार के अनुचित समाकलों को अलग तरह से परिभाषित किया गया है [ एक; बी].

1) मान लीजिए फलन एफ(एक्स) एकीकरण डोमेन के कुछ आंतरिक बिंदु पर एक अनंत असंततता है ( सीÎ( एक; बी)) खंड के अन्य बिंदुओं पर [ एक; बी] फ़ंक्शन को निरंतर माना जाता है।

फिर, यदि सीमाएं और मौजूद हैं और सीमित हैं, तो हम कहते हैं कि अभिन्न अभिसरण होता है और बराबर होता है

. (8.22)
2) फ़ंक्शन का एकमात्र असंततता बिंदु दें एफ(एक्स) बिंदु के साथ मेल खाता है एक

. (8.23)
3) माना फलन का एकमात्र असंततता बिंदु एफ(एक्स) बिंदु के साथ मेल खाता है बी. फिर, यदि सीमा मौजूद है और सीमित है, तो हम कहते हैं कि अभिन्न अभिसरण होता है और बराबर होता है

. (8.24)
यह हर जगह माना जाता है कि ई> 0 और डी> 0।

समस्या 8.12.अनुचित अभिन्न की गणना करें।

समाधान। एक्स= 2. इसलिए,

समस्या 8.13.अनुचित अभिन्न की गणना करें।

समाधान।इंटीग्रैंड में बिंदु पर दूसरी तरह की एक निरंतरता है एक्स= 0 (एकीकरण के क्षेत्र के अंदर)। फलस्वरूप,

पहली सीमा मौजूद है और परिमित है, लेकिन दूसरी सीमा अनंत (पर) के बराबर है। इसलिए, यह अभिन्न विचलन करता है।

अध्याय 9

9.1. परिभाषा एन-आयामी यूक्लिडियन अंतरिक्ष आर एन।

कई चरों के कार्यों के अध्ययन के लिए आगे बढ़ने से पहले, अवधारणा को पेश करना उपयोगी है एनकिसी के लिए -आयामी स्थान एन = 1, 2, 3,… .

2 बिंदु एक्स एन-आयामी अंतरिक्ष (वेक्टर) एक आदेशित संग्रह है एनवास्तविक संख्या।

नंबर कहा जाता है मैं-वेक्टर का निर्देशांक।

2 दो बिंदुओं के बीच की दूरी एन-आयामी स्थान और सूत्र द्वारा निर्धारित किया जाता है:

बिंदु से बिंदु की दूरी एक्सवेक्टर का मापांक कहा जाता है एक्सऔर निरूपित किया जाता है। सूत्र (9.1) से यह इस प्रकार है।

पर एन-आयामी अंतरिक्ष, अदिश उत्पाद की धारणा स्वाभाविक रूप से पेश की जाती है:

वैक्टर के बीच का कोण एक्सतथा आपसूत्र द्वारा निर्धारित किया जा सकता है:

पहले की तरह, वैक्टर एक्सतथा आपलंबवत हैं यदि और केवल यदि उनका डॉट उत्पाद शून्य है।

2सभी बिंदुओं का संग्रह एन-आयामी स्थान जिसमें दूरी को सूत्र (9.1) के अनुसार परिभाषित किया जाता है और अदिश उत्पाद कहा जाता है एन-आयामी यूक्लिडियन वेक्टर अंतरिक्ष और द्वारा निरूपित किया जाता है।

कब एन= 1 स्थान रेखा के साथ संपाती है, स्थिति में एन= 2 - एक विमान के साथ, और मामले में एन= 3 - अंतरिक्ष के साथ।

2 चलो और । सभी बिन्दुओं के समुच्चय को इस प्रकार कहा जाता है एन-आयामी गेंद एक बिंदु पर केंद्रित होती है एक्सया इ-एक बिंदु का पड़ोस एक्सअंतरिक्ष में और द्वारा निरूपित किया जाता है।

समन्वय रूप में, यह परिभाषा इस तरह दिखती है:

एक सीधी रेखा के मामले में, अर्थात्। पर एन= 1, बिंदु का पड़ोस त्रिज्या के बिंदु पर केंद्रित एक अंतराल है इ. एक विमान के मामले में, यानी। पर एन= 2, बिंदु का पड़ोस त्रिज्या के बिंदु पर केंद्रित एक खुला वृत्त है इ. अंतरिक्ष के मामले में, अर्थात्। पर एन= 3 बिंदु का पड़ोस त्रिज्या के बिंदु पर केंद्रित एक खुली गेंद है इ.

9.2। कई चर के एक समारोह का दायरा। निरंतरता

2 समारोह एनचरों को ऐसा नियम (कानून) कहा जाता है, जिसके अनुसार प्रत्येक समुच्चय एनकुछ क्षेत्र से लिए गए चर डी नहीं-आयामी स्थान , एक एकल संख्या असाइन की गई है जेड. सबसे सरल मामले में।

2 2 चरों का एक फलन एक नियम (कानून) है जिसके अनुसार प्रत्येक बिंदु एम(एक्स; आप) किसी क्षेत्र से संबंधित डीविमान xOy, एक ही नंबर सौंपा गया है जेड.

निर्देशांक के साथ अंतरिक्ष में बिंदुओं का एक सेट एक निश्चित सतह (चित्र 9.1) बनाता है, जो क्षेत्र से ऊपर उठता है डी(दो चरों के फलन का ज्यामितीय अर्थ)।

2 क्षेत्र डी, जिसके लिए उपरोक्त पत्राचार का निर्माण किया गया है, फ़ंक्शन का डोमेन कहलाता है।

समस्या 9.1।फ़ंक्शन का दायरा खोजें

समाधान।परिभाषा का वांछित क्षेत्र समतल पर बिंदुओं का एक समूह है xOy, असमानताओं की प्रणाली को संतुष्ट करना। असमानताएँ और निम्नलिखित पंक्तियों के प्रतिच्छेदन पर उनके चिन्ह को विपरीत (क्रमशः) में बदलें: एक्स = आपतथा एक्स = 0, आप= 0. ये रेखाएँ तल को तोड़ती हैं xOy 6 क्षेत्रों के लिए। क्रमिक रूप से, प्रत्येक क्षेत्र से सिस्टम में मनमाने बिंदुओं को प्रतिस्थापित करते हुए, हम यह सुनिश्चित करते हैं कि क्षेत्रों का संघ (1) और (3) मूल कार्य की परिभाषा का क्षेत्र है। इसके अलावा, प्रत्यक्ष एक्स = आप, बिंदु (0; 0) को छोड़कर, परिभाषा के क्षेत्र में शामिल है, और रेखाएं एक्स= 0, और आप= 0 - शामिल नहीं है (चित्र 9.2)।

2 किसी क्षेत्र का बंद होना अंतरिक्ष में बिंदुओं का एक समूह है, जिसमें से प्रत्येक के पड़ोस में क्षेत्र के बिंदु होते हैं डी.

चलो, उदाहरण के लिए, डी- विमान पर कुछ खुला (सीमा शामिल नहीं है) क्षेत्र xOy. तब क्षेत्र का समापन प्राप्त किया जाएगा यदि क्षेत्र के लिए डीउसकी सीमा संलग्न करें जी .

2 चलो किसी क्षेत्र में डीविमान xOyएक फ़ंक्शन दिया गया है, और क्षेत्र के कुछ बंद होने दें डी()। संख्या लेकिनबिंदु पर फलन की सीमा कहलाती है एम 0 अगर किसी संख्या के लिए इ> 0 ऐसी एक संख्या है δ > 0, जो बिंदु के अलावा अन्य सभी बिंदुओं के लिए है एम 0 और इससे दूर . से कम δ , असमानता संतुष्ट है।

2 एक फ़ंक्शन को एक बिंदु पर निरंतर कहा जाता है यदि इसे इस बिंदु () पर परिभाषित किया जाता है और समानता होती है।

§9.3। दो चरों के फलन की स्तर रेखाएँ

विमान पर 2 पंक्तियाँ xOy, समीकरणों द्वारा दिया गया है, जहां सेएक मनमाना स्थिरांक है, फलन की समतल रेखाएँ कहलाती हैं।

स्तर रेखाएँ एक सतह, किसी दिए गए फ़ंक्शन और एक समतल के प्रतिच्छेदन की रेखाएँ होती हैं जेड = सी, विमान के समानांतर xOy. समतल रेखाओं की सहायता से आप फलन द्वारा दी गई सतह के आकार का अध्ययन कर सकते हैं।

उदाहरण 9.2।समतल रेखाएँ ज्ञात कीजिए और समीकरण द्वारा दी गई सतह की आकृति ज्ञात कीजिए।

इस मामले में स्तर रेखाओं के समीकरणों का रूप है। सी पर< 0 уравнение дает пустое множество решений (следовательно, вся поверхность расположена выше плоскости xOy) पर सी= 0 केवल एक बिंदु स्तर रेखा के समीकरण को संतुष्ट करता है एक्स = 0, आप= 0 (विमान के साथ xOyसतह केवल मूल बिंदु पर प्रतिच्छेद करती है)। पर सी> 0 स्तर की रेखाएं अर्ध-अक्ष वाली दीर्घवृत्त होती हैं और . विभिन्न मूल्यों के अनुरूप स्तर रेखाएँ से, अंजीर में दिखाया गया है। 9.3. समीकरण द्वारा दी गई सतह को अण्डाकार परवलयिक कहा जाता है (चित्र 9.4)।

9.4. पहले आदेश का आंशिक व्युत्पन्न

चलो कुछ क्षेत्र में डीविमान xOyफ़ंक्शन दिया गया है, और यह क्षेत्र का कुछ बिंदु है डी.

एक्स

, (9.2)

2 एक चर के संबंध में एक बिंदु पर एक फ़ंक्शन का आंशिक व्युत्पन्न आप(निहित या ) कहा जाता है

, (9.3)
यदि दी गई सीमा मौजूद है और परिमित है।

2 किसी फ़ंक्शन का आंशिक व्युत्पन्न एनचर द्वारा बिंदु पर चर एक्स मैंबुलाया

, (9.4)
यदि दी गई सीमा मौजूद है और परिमित है।

जैसा कि सूत्रों (9.2) - (9.4) से देखा जा सकता है, आंशिक व्युत्पन्न उसी तरह निर्धारित किए जाते हैं जैसे एक चर के एक फ़ंक्शन का व्युत्पन्न निर्धारित किया गया था। सीमा की गणना करते समय, केवल एक चर को बढ़ाया जाता है, अन्य चर में वृद्धि नहीं होती है और स्थिर रहता है। नतीजतन, आंशिक डेरिवेटिव की गणना सामान्य डेरिवेटिव के समान नियमों के अनुसार की जा सकती है, सभी मुक्त चर (जिसके संबंध में भेदभाव किया जाता है) को स्थिरांक के रूप में मानते हुए।

समस्या 9.3।कार्यों के आंशिक व्युत्पन्न खोजें

समाधान। .

समस्या 9.4।किसी फ़ंक्शन के आंशिक व्युत्पन्न खोजें।

समाधान।चर के संबंध में इस फ़ंक्शन को अलग करते समय एक्सहम एक शक्ति फ़ंक्शन के भेदभाव के नियम का उपयोग करते हैं, और जब एक चर के संबंध में आंशिक व्युत्पन्न पाते हैं आप- घातीय फ़ंक्शन के भेदभाव का नियम:

समस्या 9.5.बिंदु पर फ़ंक्शन के आंशिक व्युत्पन्न की गणना करें।

समाधान।एक जटिल फलन के विभेदीकरण के नियम को लागू करने पर, हम आंशिक अवकलज पाते हैं

आंशिक व्युत्पन्न में बिंदु के निर्देशांक को प्रतिस्थापित करना एम, हम पाते हैं

9.5. कई चर का ढाल कार्य।
दिशात्मक व्युत्पन्न

2 किसी बिंदु पर किसी फ़ंक्शन का ग्रेडिएंट एक वेक्टर होता है जो किसी दिए गए बिंदु पर गणना किए गए फ़ंक्शन के आंशिक डेरिवेटिव से बना होता है:

2 वेक्टर की दिशा में एक बिंदु पर एक फ़ंक्शन का व्युत्पन्न इस फ़ंक्शन के ग्रेडिएंट वेक्टर का प्रक्षेपण है, जिसकी गणना बिंदु पर की जाती है एम 0 , इस दिशा में

सूत्र (2.6) के अनुसार एक वेक्टर पर एक वेक्टर के प्रक्षेपण की गणना करते हुए, हम प्राप्त करते हैं

. (9.7)
यह देखते हुए कि जहां एकवह कोण है जो वेक्टर अक्ष के साथ बनाता है बैल, हम वेक्टर की दिशा के संबंध में व्युत्पन्न की गणना के लिए एक और सूत्र प्राप्त करते हैं

समस्या 9.6।किसी बिंदु पर किसी फ़ंक्शन का ग्रेडिएंट खोजें एम 0 (4; 2) और वेक्टर की दिशा में व्युत्पन्न

समाधान।आइए आंशिक व्युत्पन्न खोजें

बिंदु पर आंशिक डेरिवेटिव के मूल्यों की गणना करें एम 0:

एक बिंदु पर फंक्शन ग्रेडिएंट एम 0 हम सूत्र (9.5) से पाते हैं:

समस्या 9.7।बिंदु पर एम 0 (0; 1) दूसरे समन्वय कोण के द्विभाजक की दिशा में फ़ंक्शन के व्युत्पन्न की गणना करें।

समाधान।आइए फ़ंक्शन के आंशिक व्युत्पन्न खोजें:

एक बिंदु पर आंशिक डेरिवेटिव और फ़ंक्शन के ग्रेडिएंट के मूल्यों की गणना करें एम 0:

एक बिंदु पर एक समारोह का व्युत्पन्न एम 0 दूसरे निर्देशांक कोण के द्विभाजक की दिशा में (यह दिशा अक्ष के साथ है बैलकोना एक= 135°) हम सूत्र (9.8) से पाते हैं:

§9.6। कई चर के एक समारोह का अंतर
और अनुमानित गणना के लिए इसका आवेदन

1 यदि बिंदु पर फ़ंक्शन में निरंतर आंशिक व्युत्पन्न है और, तो बिंदु से गुजरते समय इसकी कुल वृद्धि एम 0 से एक बिंदु के रूप में दर्शाया जा सकता है:

, (9.9)
जहां पर , ।

2 व्यंजक को बिंदु पर फलन का कुल अंतर कहते हैं।

सूत्र (9.9) से यह इस प्रकार है कि फ़ंक्शन का अंतर फ़ंक्शन की कुल वृद्धि का मुख्य रैखिक भाग है। पर्याप्त रूप से छोटे D . के लिए एक्सऔर डी आपअभिव्यक्ति अंतर से बहुत छोटी है और इसे उपेक्षित किया जा सकता है। इस प्रकार, हम निम्नलिखित अनुमानित सूत्र पर पहुँचते हैं:

. (9.10)
टिप्पणी।सूत्र (9.10) का उपयोग केवल बिंदु के काफी करीब बिंदुओं पर कार्यों के मूल्यों की अनुमानित गणना के लिए किया जा सकता है। मान जितना छोटा होगा, सूत्र (9.9) द्वारा पाया गया मान उतना ही सटीक होगा।

उदाहरण 9.8.अंतर का उपयोग करके लगभग गणना करें।

आइए एक समारोह पर विचार करें। मूल्य की गणना करना आवश्यक है जेडइस फ़ंक्शन का 1 बिंदु पर ( एक्स 1 ; आप 1) = (0.09; 6.95)। आइए हम बिंदु (0; 7) को एक बिंदु के रूप में चुनते हुए अनुमानित सूत्र (9.9) का उपयोग करें। फिर डी एक्स = एक्स 1 – एक्स 0 = 0.09 - 0 = 0.09, डी आप =आप 1 – आप 0 = 6,95 – 7 = – 0,05.

फलस्वरूप,

9.7. उच्च ऑर्डर के आंशिक डेरिवेटिव

क्षेत्र में चलो डीएक फ़ंक्शन दिया जाता है जिसमें निरंतर आंशिक व्युत्पन्न होते हैं और इस क्षेत्र में। इस प्रकार क्षेत्र में डीहमने दो चरों के दो नए निरंतर फलन प्राप्त किए हैं और . यदि क्षेत्र में किसी बिंदु पर डीकार्य करता है और चर के संबंध में आंशिक व्युत्पन्न होता है एक्स, और परिवर्तन से आप, तब इन अवकलजों को फलन का द्वितीय कोटि अवकलज कहा जाता है। उन्हें निम्नानुसार नामित किया गया है:

1 यदि क्षेत्र में किसी बिंदु पर डीफ़ंक्शन में निरंतर मिश्रित व्युत्पन्न होते हैं और, फिर बिंदु पर ये डेरिवेटिव बराबर होते हैं:। डी, निम्नलिखित शर्तों को पूरा किया जाना चाहिए: डी = 32 - 9 = 23।

चूँकि विवेचक शून्य से बड़ा है, तो बिंदु पर एमफ़ंक्शन में एक चरम है। अर्थात्, एक स्थानीय न्यूनतम, चूंकि लेकिनतथा सेशून्य से ऊपर। जिसमें

पहली तरह के अनुचित अभिन्न।वास्तव में, यह वही निश्चित समाकलन है, लेकिन ऐसे मामलों में जहां समाकलकों की एक अनंत ऊपरी या निचली समाकलन सीमा होती है, या दोनों समाकलन सीमाएँ अनंत होती हैं।

दूसरे प्रकार के अनुचित समाकलन।वास्तव में, यह वही निश्चित समाकलन है, लेकिन ऐसे मामलों में जहां समाकलन असीमित फलनों से लिया जाता है, समाकलन का परिमित खंड के परिमित बिंदुओं पर कोई एकीकरण नहीं होता है, जो अनंत में बदल जाता है।

तुलना के लिए।एक निश्चित अभिन्न की अवधारणा को पेश करते समय, यह माना गया था कि कार्य एफ(एक्स) खंड पर निरंतर है [ एक, बी], और एकीकरण का अंतराल परिमित है, अर्थात यह संख्याओं द्वारा सीमित है, न कि अनंत द्वारा। कुछ कार्य इन प्रतिबंधों को छोड़ने की आवश्यकता की ओर ले जाते हैं। इस प्रकार अनुचित समाकलन प्रकट होते हैं।

अनुचित अभिन्न का ज्यामितीय अर्थकाफी सरल हो जाता है। जब फ़ंक्शन का ग्राफ आप = एफ(एक्स) अक्ष के ऊपर है बैल, निश्चित अभिन्न एक वक्र से घिरे एक वक्रीय समलम्बाकार क्षेत्र को व्यक्त करता है आप = एफ(एक्स) , एब्सिस्सा और ऑर्डिनेट्स एक्स = एक , एक्स = बी. बदले में, अनुचित अभिन्न रेखाओं के बीच संलग्न एक असीमित (अनंत) वक्रताकार समलम्बाकार के क्षेत्र को व्यक्त करता है आप = एफ(एक्स) (नीचे लाल रंग में चित्रित) एक्स = एकऔर भुज अक्ष।

अन्य अनंत अंतरालों के लिए अनुचित समाकलों को समान रूप से परिभाषित किया गया है:

एक अनंत वक्रीय समलम्ब चतुर्भुज का क्षेत्रफल एक परिमित संख्या हो सकता है, जिस स्थिति में अनुचित समाकलन अभिसरण कहलाता है। क्षेत्र अनंत भी हो सकता है, जिस स्थिति में अनुचित समाकलन को अपसारी कहते हैं।

अपने आप में अनुचित समाकलन के स्थान पर समाकलन की सीमा का प्रयोग करना।अनुचित समाकल की गणना करने के लिए, आपको निश्चित समाकल की सीमा का उपयोग करना होगा। यदि यह सीमा मौजूद है और परिमित (अनंत के बराबर नहीं) है, तो अनुचित अभिन्न को अभिसरण कहा जाता है, अन्यथा यह भिन्न होता है। सीमा चिन्ह के तहत चर क्या होता है यह इस बात पर निर्भर करता है कि हम पहली तरह के या दूसरे प्रकार के अनुचित अभिन्न के साथ काम कर रहे हैं। आइए अब इसके बारे में जानते हैं।

पहली तरह के अनुचित समाकलन - अनंत सीमाओं और उनके अभिसरण के साथ

अनंत ऊपरी सीमा के साथ अनुचित समाकलन

तो, अनुचित अभिन्न का रिकॉर्ड सामान्य निश्चित अभिन्न से भिन्न होता है कि एकीकरण की ऊपरी सीमा अनंत है।

परिभाषा। एक निरंतर कार्य से एकीकरण की अनंत ऊपरी सीमा के साथ एक अनुचित अभिन्न अंग एफ(एक्स) के बीच एक इससे पहले ∞ समाकलन की ऊपरी सीमा के साथ इस फलन के समाकलन की सीमा कहलाती है बी और एकीकरण की निचली सीमा एक बशर्ते कि एकीकरण की ऊपरी सीमा अनिश्चित काल तक बढ़े, अर्थात।

.

यदि यह सीमा मौजूद है और किसी संख्या के बराबर है, न कि अनंत के लिए, तो अनुचित अभिन्न को अभिसरण कहा जाता है, और सीमा के बराबर संख्या को इसके मान के रूप में लिया जाता है। अन्यथा अनुचित समाकलन को अपसारी कहते हैंऔर इसके लिए कोई मूल्य जिम्मेदार नहीं है।

उदाहरण 1. अनुचित समाकलन की गणना करें(यदि यह अभिसरण करता है)।

समाधान। अनुचित अभिन्न की परिभाषा के आधार पर, हम पाते हैं

चूंकि सीमा मौजूद है और 1 के बराबर है, तो दिया गया अनुचित अभिन्न अभिसरणऔर 1 के बराबर है।

निम्नलिखित उदाहरण में, इंटीग्रैंड लगभग उदाहरण 1 जैसा ही है, केवल एक्स की डिग्री दो नहीं है, लेकिन अक्षर अल्फा है, और कार्य अभिसरण के लिए अनुचित अभिन्न का अध्ययन करना है। यही है, इस सवाल का जवाब दिया जाना बाकी है: अल्फा के किन मूल्यों पर यह अनुचित अभिन्न अभिसरण होता है, और किन मूल्यों पर यह विचलन करता है?

उदाहरण 2. एक अनुचित समाकलन के अभिसरण की जाँच कीजिए(निचली एकीकरण सीमा शून्य से अधिक है)।

समाधान। मान लीजिए कि पहले , फिर

परिणामी व्यंजक में, हम सीमा पर जाते हैं:

यह देखना आसान है कि दायीं ओर की सीमा मौजूद है और शून्य के बराबर है जब, यानी, और जब मौजूद नहीं है, यानी।

पहले मामले में, यानी जब . तो अगर और मौजूद नहीं है।

हमारे अध्ययन का निष्कर्ष निम्नलिखित है: अनुचित अभिन्न अभिसरणपर और अलग करनापर ।

न्यूटन-लीबनिज़ सूत्र का अध्ययन किए गए प्रकार के अनुचित अभिन्न पर लागू करना , हम निम्नलिखित बहुत समान सूत्र प्राप्त कर सकते हैं:

.

यह सामान्यीकृत न्यूटन-लीबनिज सूत्र है।

उदाहरण 3. अनुचित समाकलन की गणना करें(यदि यह अभिसरण करता है)।

इस अभिन्न की सीमा मौजूद है:

दूसरा अभिन्न, जो मूल अभिन्न को व्यक्त करने वाला योग है:

इस अभिन्न की सीमा भी मौजूद है:

.

हम दो पूर्णांकों का योग पाते हैं, जो दो अनंत सीमाओं के साथ मूल अनुचित समाकलन का मान भी है:

दूसरे प्रकार के अनुचित समाकलन - असीमित कार्यों और उनके अभिसरण से

चलो समारोह एफ(एक्स) से खंड पर सेट करें एक इससे पहले बी और उस पर असीमित। मान लीजिए कि फलन बिंदु पर अनंत तक जाता है बी , जबकि खंड के अन्य सभी बिंदुओं पर यह निरंतर है।

परिभाषा। समारोह का अनुचित अभिन्न एफ(एक्स) से खंड पर एक इससे पहले बी समाकलन की ऊपरी सीमा के साथ इस फलन के समाकलन की सीमा कहलाती है सी , यदि प्रयास करते समय सी प्रति बी फलन अनिश्चित काल के लिए बढ़ता है, और बिंदु पर एक्स = बी फ़ंक्शन परिभाषित नहीं है, अर्थात।

.

यदि यह सीमा मौजूद है, तो दूसरी तरह के अनुचित अभिन्न को अभिसरण कहा जाता है, अन्यथा भिन्न।

न्यूटन-लीबनिज सूत्र का उपयोग करते हुए, हम प्राप्त करते हैं।