Du dydžiai vadinami tiesiogiai proporcingas, jei vieną iš jų padidinus kelis kartus, kitas didinamas tiek pat. Atitinkamai, kai vienas iš jų sumažėja kelis kartus, kitas sumažėja tiek pat.

Ryšys tarp tokių dydžių yra tiesioginis proporcingas ryšys. Tiesioginio proporcingo ryšio pavyzdžiai:

1) esant pastoviam greičiui, nuvažiuotas atstumas yra tiesiogiai proporcingas laikui;

2) kvadrato perimetras ir jo kraštinė yra tiesiogiai proporcingi;

3) viena kaina perkamos prekės savikaina yra tiesiogiai proporcinga jos kiekiui.

Norėdami atskirti tiesioginį proporcingą ryšį nuo atvirkštinio, galite naudoti patarlę: „Kuo toliau į mišką, tuo daugiau malkų“.

Patogu spręsti tiesiogiai proporcingų dydžių uždavinius naudojant proporcijas.

1) 10 dalių gamybai reikia 3,5 kg metalo. Kiek metalo bus sunaudota 12 tokių dalių pagaminti?

(Mes ginčijamės taip:

1. Užpildytame stulpelyje padėkite rodyklę kryptimi nuo didžiausio skaičiaus iki mažiausio.

2. Kuo daugiau dalių, tuo daugiau metalo reikia joms pagaminti. Taigi tai yra tiesiogiai proporcingas santykis.

Tegul x kg metalo reikia 12 dalių pagaminti. Sudarome proporciją (kryptimi nuo rodyklės pradžios iki jos pabaigos):

12:10=x:3,5

Norėdami rasti , turime padalyti kraštutinių terminų sandaugą iš žinomo vidurinio termino:

Tai reiškia, kad reikės 4,2 kg metalo.

Atsakymas: 4,2 kg.

2) Už 15 metrų audinio buvo sumokėta 1680 rublių. Kiek kainuoja 12 metrų tokio audinio?

(1. Užpildytame stulpelyje nukreipkite rodyklę kryptimi nuo didžiausio skaičiaus iki mažiausio.

2. Kuo mažiau audinio perkate, tuo mažiau už jį turėsite mokėti. Taigi tai yra tiesiogiai proporcingas santykis.

3. Todėl antroji rodyklė nukreipta ta pačia kryptimi kaip ir pirmoji).

Tegul x rubliai kainuoja 12 metrų audinio. Sudarome proporciją (nuo rodyklės pradžios iki jos pabaigos):

15:12=1680:x

Norėdami rasti nežinomą kraštutinį proporcijos narį, padalijame vidurinių dalių sandaugą iš žinomo kraštutinio proporcijos nario:

Taigi, 12 metrų kainavo 1344 rublius.

Atsakymas: 1344 rubliai.

Linijinė funkcija

Linijinė funkcija yra funkcija, kurią galima pateikti pagal formulę y = kx + b,

kur x yra nepriklausomas kintamasis, k ir b yra kai kurie skaičiai.

Tiesinės funkcijos grafikas yra tiesi linija.

Iškviečiamas skaičius k tiesios linijos nuolydis– funkcijos y = kx + b grafikas.

Jei k > 0, tai tiesės y = kx + b pasvirimo kampas į ašį X aštrus; jei k< 0, то этот угол тупой.

Jei tiesių, kurios yra dviejų tiesinių funkcijų grafikai, nuolydžiai yra skirtingi, tada šios linijos susikerta. O jei šlaitai vienodi, tai linijos lygiagrečios.

Funkcijų grafikas y=kx +b, kur k ≠ 0, yra tiesė, lygiagreti tiesei y = kx.

tiesioginė proporcija.

Tiesioginis proporcingumas yra funkcija, kurią galima nurodyti formule y = kx, kur x yra nepriklausomas kintamasis, k yra skaičius, kuris skiriasi nuo nulio. Iškviečiamas skaičius k tiesioginio proporcingumo koeficientas.

Tiesioginio proporcingumo grafikas yra tiesė, einanti per pradžią (žr. pav.).

Tiesioginis proporcingumas yra ypatingas tiesinės funkcijos atvejis.

Funkcijų savybėsy=kx:

Atvirkštinis proporcingumas

Atvirkštinis proporcingumas yra funkcija, kurią galima apibrėžti pagal formulę:

k
y=-
x

kur x yra nepriklausomas kintamasis ir k yra ne nulis skaičius.

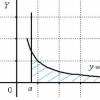
Atvirkščiai proporcingas grafikas yra kreivė, vadinama hiperbolė(žr. paveikslėlį).

Kreivės, kuri yra šios funkcijos grafikas, ašys x ir y veikia kaip asimptotas. Asimptotė yra tiesi linija, prie kurios artėja kreivės taškai, kai jie tolsta į begalybę.

k
Funkcijų savybėsy=-:
x

Tiesioginio proporcingumo samprata

Įsivaizduokite, kad galvojate nusipirkti savo mėgstamą saldainį (arba ką tik mėgstate). Saldainiai parduotuvėje turi savo kainą. Tarkime, 300 rublių už kilogramą. Kuo daugiau saldainių perkate, tuo daugiau pinigų sumokėsite. Tai jei nori 2 kilogramų – mokėk 600 rublių, o jei nori 3 kilogramų – duok 900 rublių. Atrodo, kad viskas čia aišku, tiesa?

Jei taip, dabar jums aišku, kas yra tiesioginis proporcingumas – tai sąvoka, apibūdinanti dviejų vienas nuo kito priklausomų dydžių santykį. Ir šių dydžių santykis išlieka nepakitęs ir pastovus: kiek dalių viena iš jų didėja arba mažėja, tiek pat dalių proporcingai didėja arba mažėja antra.

Tiesioginį proporcingumą galima apibūdinti tokia formule: f(x) = a*x, o a šioje formulėje yra pastovi reikšmė (a = const). Mūsų saldainių pavyzdyje kaina yra konstanta, konstanta. Jis nedidėja ir nemažėja, kad ir kiek saldumynų nuspręstumėte nusipirkti. Nepriklausomas kintamasis (argumentas) x yra tai, kiek kilogramų saldumynų ketinate pirkti. Ir priklausomas kintamasis f(x) (funkcija) yra tai, kiek pinigų galiausiai sumokėsite už pirkinį. Taigi galime pakeisti skaičius formulėje ir gauti: 600 r. = 300 r. * 2 kg.

Tarpinė išvada tokia: jei argumentas didėja, funkcija taip pat didėja, jei argumentas mažėja, funkcija taip pat mažėja

Funkcija ir jos savybės

Tiesioginė proporcinga funkcija yra ypatingas tiesinės funkcijos atvejis. Jei tiesinė funkcija yra y = k*x + b, tai tiesioginiam proporcingumui ji atrodo taip: y = k*x, kur k vadinamas proporcingumo koeficientu, ir tai visada yra ne nulis skaičius. Apskaičiuoti k yra paprasta – jis randamas kaip funkcijos ir argumento koeficientas: k = y/x.

Kad būtų aiškiau, paimkime kitą pavyzdį. Įsivaizduokite, kad automobilis juda iš taško A į tašką B. Jo greitis yra 60 km/val. Jei darome prielaidą, kad judėjimo greitis išlieka pastovus, tada jį galima laikyti konstanta. Tada parašome sąlygas forma: S \u003d 60 * t, ir ši formulė yra panaši į tiesioginio proporcingumo funkciją y \u003d k * x. Nubrėžkime paralelę toliau: jei k \u003d y / x, tada automobilio greitį galima apskaičiuoti žinant atstumą tarp A ir B ir laiką, praleistą kelyje: V \u003d S / t.

O dabar nuo tiesioginio proporcingumo žinių pritaikymo grįžkime prie jo funkcijos. Kurių savybės apima:

jo apibrėžimo sritis yra visų realiųjų skaičių aibė (taip pat ir jos poaibis);

funkcija nelyginė;

kintamųjų pokytis yra tiesiogiai proporcingas visam skaičių eilutės ilgiui.

Tiesioginis proporcingumas ir jo grafikas

Tiesioginės proporcingos funkcijos grafikas yra tiesė, kertanti pradžios tašką. Norėdami jį pastatyti, pakanka pažymėti dar vieną tašką. Ir prijunkite jį ir linijos kilmę.

Grafo atveju k yra nuolydis. Jei nuolydis mažesnis už nulį (k< 0), то угол между графиком функции прямой пропорциональности и осью абсцисс тупой, а функция убывающая. Если угловой коэффициент больше нуля (k >0), grafikas ir x ašis sudaro smailųjį kampą, o funkcija didėja.

Ir dar viena tiesioginio proporcingumo funkcijos grafiko savybė yra tiesiogiai susijusi su nuolydžiu k. Tarkime, kad turime dvi neidentiškas funkcijas ir atitinkamai du grafikus. Taigi, jei šių funkcijų koeficientai k yra lygūs, jų grafikai yra lygiagretūs koordinačių ašyje. O jei koeficientai k nelygūs vienas kitam, grafikai susikerta.

Užduočių pavyzdžiai

Nuspręskime porą tiesioginio proporcingumo problemų

Pradėkime nuo paprasto.

1 užduotis: Įsivaizduokite, kad 5 vištos per 5 dienas padėjo 5 kiaušinius. O jei vištų yra 20, kiek kiaušinių jos padės per 20 dienų?

Sprendimas: Nežinomąjį pažymėkite kaip x. Ir samprotuosime taip: kiek kartų buvo daugiau vištų? Padalinkite 20 iš 5 ir sužinokite, kad tai 4 kartus. O kiek kartų daugiau kiaušinių padės 20 vištų per tas pačias 5 dienas? Taip pat 4 kartus daugiau. Taigi, savo randame taip: 5 * 4 * 4 \u003d per 20 dienų 20 vištų padės 80 kiaušinių.

Dabar pavyzdys yra šiek tiek sudėtingesnis, perfrazuokime užduotį iš Newtono „Bendrosios aritmetikos“. 2 užduotis: Rašytojas gali parašyti 14 puslapių naujos knygos per 8 dienas. Jei jis turėtų padėjėjų, kiek žmonių reikėtų parašyti 420 puslapių per 12 dienų?

Sprendimas: Manome, kad žmonių (rašytojo + padėjėjų) skaičius didėja didėjant darbų kiekiui, jei jį reikia atlikti per tiek pat laiko. Bet kiek kartų? Padalinę 420 iš 14, sužinome, kad jis padidėja 30 kartų. Bet kadangi pagal užduoties sąlygą darbui skiriama daugiau laiko, padėjėjų skaičius nepadidėja 30 kartų, o tokiu būdu: x \u003d 1 (rašytojas) * 30 (kartų): 12/8 (dienos). Transformuokime ir išsiaiškinkime, kad x = 20 žmonių per 12 dienų parašys 420 puslapių.

Išspręskime kitą problemą, panašią į tas, kurias turėjome pavyzdžiuose.

3 užduotis: du automobiliai išvyko į tą pačią kelionę. Vienas judėjo 70 km/h greičiu ir tą patį atstumą įveikė per 2 val., kaip ir kitas per 7 val. Raskite antrojo automobilio greitį.

Sprendimas: Kaip prisimenate, kelias nustatomas pagal greitį ir laiką - S = V *t. Kadangi abu automobiliai įveikė tą patį atstumą, galime sutapatinti dvi išraiškas: 70*2 = V*7. Kur randame, kad antrojo automobilio greitis V = 70*2/7 = 20 km/h.

Ir dar pora užduočių su tiesioginio proporcingumo funkcijomis pavyzdžių. Kartais uždaviniuose reikia rasti koeficientą k.

4 užduotis: atsižvelgiant į funkcijas y \u003d - x / 16 ir y \u003d 5x / 2, nustatykite jų proporcingumo koeficientus.

Sprendimas: kaip prisimenate, k = y/x. Taigi pirmosios funkcijos koeficientas yra -1/16, o antrosios - k = 5/2.

Taip pat galite susidurti su tokia užduotimi kaip 5 užduotis: užsirašykite tiesioginio proporcingumo formulę. Jo grafikas ir funkcijos y \u003d -5x + 3 grafikas yra lygiagrečiai.

Sprendimas: funkcija, kuri mums suteikta sąlygoje, yra tiesinė. Žinome, kad tiesioginis proporcingumas yra ypatingas tiesinės funkcijos atvejis. Taip pat žinome, kad jei k funkcijų koeficientai yra lygūs, jų grafikai yra lygiagretūs. Tai reiškia, kad viskas, ko reikia, yra apskaičiuoti žinomos funkcijos koeficientą ir nustatyti tiesioginį proporcingumą naudojant mums žinomą formulę: y \u003d k * x. Koeficientas k \u003d -5, tiesioginis proporcingumas: y \u003d -5 * x.

Išvada

Dabar jūs sužinojote (arba prisiminėte, jei jau nagrinėjote šią temą anksčiau), kas vadinama tiesioginis proporcingumas, ir svarstė pavyzdžių. Taip pat kalbėjome apie tiesioginio proporcingumo funkciją ir jos grafiką, išsprendėme, pavyzdžiui, keletą problemų.

Jei šis straipsnis buvo naudingas ir padėjo suprasti temą, papasakokite apie tai komentaruose. Kad žinotume, ar galime jums būti naudingi.

svetainę, visiškai ar iš dalies nukopijavus medžiagą, būtina nuoroda į šaltinį.

Priklausomybės tipai

Apsvarstykite galimybę įkrauti akumuliatorių. Kaip pirmąją vertę, paimkime laiką, kurio reikia įkrovimui. Antroji reikšmė yra laikas, per kurį jis veiks po įkrovimo. Kuo ilgiau akumuliatorius kraunamas, tuo ilgiau jis tarnaus. Procesas tęsis tol, kol baterija bus visiškai įkrauta.

Baterijos veikimo trukmės priklausomybė nuo įkrovimo laiko

1 pastaba

Ši priklausomybė vadinama tiesiai:

Didėjant vienai reikšmei, didėja ir kita. Vienai reikšmei mažėjant, mažėja ir kita.

Panagrinėkime kitą pavyzdį.

Kuo daugiau knygų mokinys perskaitys, tuo mažiau diktante padarys klaidų. Arba kuo aukščiau kopsite į kalnus, tuo žemesnis bus atmosferos slėgis.

2 pastaba

Ši priklausomybė vadinama atvirkščiai:

Kai viena vertė didėja, kita mažėja. Kai viena vertė mažėja, kita reikšmė didėja.

Taigi byloje tiesioginė priklausomybė abu dydžiai keičiasi vienodai (tiek didėja, tiek mažėja), o tuo atveju atvirkštinis ryšys- priešingai (vienas didėja, o kitas mažėja, arba atvirkščiai).

Priklausomybių tarp dydžių nustatymas

1 pavyzdys

Laikas, kurio reikia norint aplankyti draugą, yra 20 USD minučių. Padidinus greitį (pirmosios vertės) $2$ kartus, pamatysime, kaip pasikeis laikas (antra reikšmė), kuris bus praleistas kelyje pas draugą.

Akivaizdu, kad laikas sumažės 2 USD kartų.

3 pastaba

Ši priklausomybė vadinama proporcingas:

Kiek kartų keičiasi viena reikšmė, kiek kartų pasikeis antroji.

2 pavyzdys

Už 2 USD duonos kepalą parduotuvėje reikia sumokėti 80 rublių. Jei jums reikia nusipirkti 4 USD duonos kepalų (duonos kiekis padidėja 2 USD kartus), kiek daugiau turėsite sumokėti?

Akivaizdu, kad kaina taip pat padidės 2 USD kartus. Turime proporcingos priklausomybės pavyzdį.

Abiejuose pavyzdžiuose buvo nagrinėjamos proporcingos priklausomybės. Tačiau pavyzdyje su duonos kepalais vertės keičiasi viena kryptimi, todėl priklausomybė yra tiesiai. O pavyzdyje su kelione pas draugą greičio ir laiko santykis yra toks atvirkščiai. Taigi, yra tiesiogiai proporcingas santykis ir atvirkščiai proporcingas ryšys.

Tiesioginis proporcingumas

Apsvarstykite 2 USD proporcingus kiekius: duonos kepalų skaičių ir jų kainą. Tegul duonos kepaliukai 2 USD kainuoja 80 USD rublių. Ritimų skaičiui padidėjus 4 USD kartus (8 USD ritinėliai), jų bendra kaina bus 320 USD.

Ritimų skaičiaus santykis: $\frac(8)(2)=4$.

Ritinio kainos santykis: $\frac(320)(80)=4$.

Kaip matote, šie santykiai yra lygūs vienas kitam:

$\frac(8)(2)=\frac(320)(80)$.

1 apibrėžimas

Dviejų santykių lygybė vadinama proporcija.

Esant tiesiogiai proporcingam ryšiui, santykis gaunamas, kai pirmosios ir antrosios verčių pokytis yra toks pat:

$\frac(A_2)(A_1)=\frac(B_2)(B_1)$.

2 apibrėžimas

Du dydžiai vadinami tiesiogiai proporcingas jeigu keičiant (didinant ar mažinant) vieną iš jų kita reikšmė pasikeičia (atitinkamai didėja arba mažėja) tiek pat.

3 pavyzdys

Automobilis nuvažiavo 180 USD km per 2 USD valandas. Raskite laiką, per kurį jis įveikia 2 USD padaugintą atstumą tuo pačiu greičiu.

Sprendimas.

Laikas yra tiesiogiai proporcingas atstumui:

$t=\frac(S)(v)$.

Kiek kartų padidės atstumas, esant pastoviam greičiui, laikas padidės tiek pat:

$\frac(2S)(v)=2t$;

$\frac(3S)(v)=3t$.

Automobilis nuvažiavo 180 USD km – per 2 USD valandą

Automobilis nuvažiuoja 180 USD \cdot 2=360 USD km – per $x$ valandas

Kuo daugiau atstumo automobilis nuvažiuos, tuo daugiau laiko užtruks. Todėl santykis tarp kiekių yra tiesiogiai proporcingas.

Padarykime proporciją:

$\frac(180)(360)=\frac(2)(x)$;

$x=\frac(360 \cdot 2)(180)$;

Atsakymas: Automobiliui reikės 4 USD valandų.

Atvirkštinis proporcingumas

3 apibrėžimas

Sprendimas.

Laikas atvirkščiai proporcingas greičiui:

$t=\frac(S)(v)$.

Kiek kartų greitis didėja tuo pačiu keliu, laikas sumažėja tiek pat:

$\frac(S)(2v)=\frac(t)(2)$;

$\frac(S)(3v)=\frac(t)(3)$.

Parašykime problemos sąlygą lentelės pavidalu:

Automobilis nuvažiavo 60 USD km – per 6 USD valandas

Automobilis nuvažiuoja $120$ km – per $x$ valandas

Kuo greitesnis automobilis, tuo mažiau laiko užtruks. Todėl santykis tarp dydžių yra atvirkščiai proporcingas.

Padarykime proporciją.

Nes proporcingumas yra atvirkštinis, antrąjį santykį paverčiame proporcingai:

$\frac(60)(120)=\frac(x)(6)$;

$x=\frac(60 \cdot 6)(120)$;

Atsakymas: Automobiliui reikės 3 USD valandų.

Šiandien pažiūrėsime, kokie dydžiai vadinami atvirkščiai proporcingais, kaip atrodo atvirkštinio proporcingumo grafikas ir kuo visa tai gali būti jums naudinga ne tik matematikos pamokose, bet ir už mokyklos sienų.

Tokios skirtingos proporcijos

Proporcingumasįvardykite du dydžius, kurie yra vienas nuo kito priklausomi.

Priklausomybė gali būti tiesioginė ir atvirkštinė. Todėl santykis tarp dydžių apibūdina tiesioginį ir atvirkštinį proporcingumą.

Tiesioginis proporcingumas- tai toks ryšys tarp dviejų dydžių, kai vieno iš jų padidėjimas arba sumažėjimas lemia kito padidėjimą arba sumažėjimą. Tie. jų požiūris nesikeičia.

Pavyzdžiui, kuo daugiau pastangų įdėsite ruošdamiesi egzaminams, tuo aukštesni bus jūsų pažymiai. Arba kuo daugiau daiktų pasiimi su savimi į žygį, tuo sunkiau neštis kuprinę. Tie. pastangų, skirtų ruošiantis egzaminams, kiekis yra tiesiogiai proporcingas gautiems pažymiams. O į kuprinę sukrautų daiktų skaičius yra tiesiogiai proporcingas jos svoriui.

Atvirkštinis proporcingumas- tai funkcinė priklausomybė, kai nepriklausomos reikšmės sumažėjimas arba padidėjimas kelis kartus (tai vadinamas argumentu) sukelia proporcingą (t. y. tokiu pat dydžiu) priklausomos reikšmės padidėjimą arba sumažėjimą (tai vadinama funkcija).

Iliustruojame paprastu pavyzdžiu. Norite nusipirkti obuolių turguje. Obuoliai ant prekystalio ir pinigų suma jūsų piniginėje yra atvirkščiai susiję. Tie. kuo daugiau obuolių perkate, tuo mažiau pinigų lieka.

Funkcija ir jos grafikas

Atvirkštinio proporcingumo funkciją galima apibūdinti kaip y = k/x. Kuriame x≠ 0 ir k≠ 0.

Ši funkcija turi šias savybes:

1. Jo apibrėžimo sritis yra visų realiųjų skaičių, išskyrus x = 0. D(y): (-∞; 0) U (0; +∞).
2. Diapazoną sudaro tikrieji skaičiai, išskyrus y= 0. E(y): (-∞; 0) U (0; +∞) .
3. Jis neturi didžiausių ar minimalių verčių.
4. Yra nelyginis ir jo grafikas yra simetriškas kilmei.
5. Neperiodinis.
6. Jo grafikas nekerta koordinačių ašių.
7. Neturi nulių.
8. Jeigu k> 0 (ty argumentas didėja), funkcija proporcingai mažėja kiekviename jos intervale. Jeigu k< 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
9. Didėjant argumentui ( k> 0) funkcijos neigiamos reikšmės yra intervale (-∞; 0), o teigiamos reikšmės yra intervale (0; +∞). Kai argumentas mažėja ( k< 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

Atvirkštinės proporcingumo funkcijos grafikas vadinamas hiperbole. Pavaizduota taip:

Atvirkštinės proporcinės problemos

Kad būtų aiškiau, pažvelkime į keletą užduočių. Jos nėra pernelyg sudėtingos, o jų sprendimas padės įsivaizduoti, kas yra atvirkštinė proporcija ir kuo šios žinios gali būti naudingos kasdieniame gyvenime.

Užduotis numeris 1. Automobilis važiuoja 60 km/h greičiu. Jam prireikė 6 valandų, kad pasiektų tikslą. Kiek laiko jam prireiks įveikti tą patį atstumą, jei judės dvigubai greičiau?

Pradėti galime užrašydami formulę, kuri nusako laiko, atstumo ir greičio ryšį: t = S/V. Sutikite, tai mums labai primena atvirkštinio proporcingumo funkciją. Ir tai rodo, kad laikas, kurį automobilis praleidžia kelyje, ir jo judėjimo greitis yra atvirkščiai proporcingi.

Norėdami tai patikrinti, suraskime V 2, kuris pagal sąlygą yra 2 kartus didesnis: V 2 \u003d 60 * 2 \u003d 120 km / h. Tada apskaičiuojame atstumą pagal formulę S = V * t = 60 * 6 = 360 km. Dabar nesunku sužinoti laiką t 2, kurio iš mūsų reikia pagal uždavinio sąlygą: t 2 = 360/120 = 3 valandos.

Kaip matote, kelionės laikas ir greitis išties yra atvirkščiai proporcingi: važiuojant 2 kartus didesniu greičiu nei originalus, automobilis kelyje praleis 2 kartus mažiau laiko.

Šios problemos sprendimas taip pat gali būti parašytas kaip proporcija. Kodėl mes kuriame tokią diagramą:

↓ 60 km/h – 6 val

↓120 km/h – x h

Rodyklės rodo atvirkštinį ryšį. Ir jie taip pat siūlo, kad nustatant proporciją reikia apversti dešinę įrašo pusę: 60/120 \u003d x / 6. Iš kur gauname x \u003d 60 * 6/120 \u003d 3 valandas.

Užduotis numeris 2. Ceche dirba 6 darbuotojai, kurie su tam tikru darbo kiekiu susidoroja per 4 valandas. Jei darbuotojų skaičius sumažės perpus, kiek laiko užtruks, kol likę darbuotojai atliks tiek pat darbų?

Problemos sąlygas rašome vaizdinės diagramos pavidalu:

↓ 6 darbuotojai - 4 val

↓ 3 darbuotojai - x val

Parašykime tai kaip proporciją: 6/3 = x/4. Ir mes gauname x \u003d 6 * 4/3 \u003d 8 valandas. Jei darbuotojų bus 2 kartus mažiau, likusieji skirs 2 kartus daugiau laiko visam darbui atlikti.

Užduotis numeris 3. Į baseiną veda du vamzdžiai. Per vieną vamzdį vanduo patenka 2 l/s greičiu ir užpildo baseiną per 45 minutes. Per kitą vamzdį baseinas bus užpildytas per 75 minutes. Kaip greitai šiuo vamzdžiu vanduo patenka į baseiną?

Pirmiausia visus mums duotus kiekius pagal problemos būklę sujungsime į tuos pačius matavimo vienetus. Norėdami tai padaryti, išreiškiame baseino užpildymo greitį litrais per minutę: 2 l / s \u003d 2 * 60 \u003d 120 l / min.

Kadangi iš tos sąlygos, kad per antrą vamzdį baseinas pildomas lėčiau, tai reiškia, kad vandens pritekėjimo greitis yra mažesnis. Atvirkštinės proporcijos akivaizdoje. Išreikškime mums nežinomą greitį x ir sudarykime tokią schemą:

↓ 120 l/min - 45 min

↓ x l/min – 75 min

Ir tada mes sudarysime proporciją: 120 / x \u003d 75/45, iš kur x \u003d 120 * 45/75 \u003d 72 l / min.

Uždavinyje baseino užpildymo greitis išreiškiamas litrais per sekundę, savo atsakymą pateikime ta pačia forma: 72/60 = 1,2 l/s.

Užduotis numeris 4. Vizitinės kortelės spausdinamos nedidelėje privačioje spaustuvėje. Spaustuvės darbuotojas dirba 42 vizitinių kortelių greičiu per valandą ir dirba pilnu etatu – 8 val. Jei jis dirbtų greičiau ir atspausdintų 48 vizitines korteles per valandą, kiek greičiau jis galėtų grįžti namo?

Mes einame patikrintu būdu ir sudarome schemą pagal problemos sąlygą, nurodydami norimą reikšmę kaip x:

↓ 42 vizitinės kortelės/val – 8 val

↓ 48 vizitinės kortelės/val. – xh

Prieš mus – atvirkščiai proporcingas santykis: kiek kartų daugiau vizitinių kortelių atspausdina spaustuvės darbuotojas per valandą, tiek pat laiko jam prireiks tam pačiam darbui atlikti. Žinodami tai, galime nustatyti proporciją:

42/48 \u003d x / 8, x \u003d 42 * 8/48 \u003d 7 valandos.

Taigi, darbus atlikęs per 7 valandas, spaustuvės darbuotojas namo galėjo vykti valanda anksčiau.

Išvada

Mums atrodo, kad šios atvirkštinio proporcingumo problemos yra tikrai paprastos. Tikimės, kad dabar jūs taip pat jas laikote. O svarbiausia – žinios apie atvirkščiai proporcingą kiekių priklausomybę jums tikrai gali praversti ne kartą.

Ne tik matematikos pamokose ir egzaminuose. Bet net ir tada, kai ruošiatės į kelionę, apsipirkti, nuspręsti per atostogas užsidirbti ir pan.

Papasakokite komentaruose, kokius atvirkštinio ir tiesioginio proporcingumo pavyzdžius pastebite aplink save. Tegul tai būna žaidimas. Pamatysite, kaip tai įdomu. Nepamirškite šiuo straipsniu „pasidalyti“ socialiniuose tinkluose, kad galėtų žaisti ir jūsų draugai bei klasės draugai.

svetainę, visiškai ar iš dalies nukopijavus medžiagą, būtina nuoroda į šaltinį.