Bu erda loyqa to'plamlarda bajarilishi mumkin bo'lgan ba'zi asosiy operatsiyalar mavjud.

1. Qo'shish loyqa to'plam LEKIN belgisi bilan belgilanadi va quyidagicha aniqlanadi:

(5.15)

Qo'shish amali mantiqiy inkorga mos keladi. Masalan, agar LEKIN loyqa to'plamning nomi, demak "A emas" deb tushuniladi (quyidagi misolga qarang).

2. Konsolidatsiya loyqa to'plamlar LEKIN va DA belgilangan A+B(yoki AÈV) va aniqlanadi :

(5.16)

Birlashma mantiqiy bog'lovchiga mos keladi " yoki". Masalan, agar LEKIN va DA loyqa to'plamlarning nomlari, keyin esa yozuv " A yoki B' deb tushuniladi A+B.

u Ko'proq dan.

Izoh: mantiqiy aloqadorligini yodda tutish kerak Ú bu kontekstda ta'rifi bo'yicha max (ya'ni ); Ù min (ya'ni) degan ma'noni anglatadi.

3. Chorraha A va DA belgilanadi AÇV va quyidagicha aniqlanadi:

(5.17)

Kesishma mantiqiy bog'lovchiga mos keladi " u", ya'ni. .

A va B \u003d AÇB(5.18)

Elementlarning a'zolik darajasini aniqlashda u yangi loyqa to'plamga, tanlang kamroq dan (yuqoridagi izohga qarang).

4. Mahsulot A va DA belgilangan AB va formula bilan aniqlanadi

(5.19)

agar (5.20)

5.5-misol. Agar a

U=1+2+…+10

A=0,8/3+1/5+0,6/6 (5.21)

B=0,7/3+1/4+0,5/6,

Bu ØA=1/1+1/2+0,2/3+1/4+0,4/6+1/7+1/8+1/9+1/10

A+B=0,8/3+1/4+1/5+0,6/6

AZV=0,7/3+0,5/6 (min m ning ikkita qiymatidan olingan)(5.22)

AB=0,56/3+0,3/6

0,4A=0,32/3+0,4/5+0,24/6

5. Dekart mahsuloti loyqa to'plamlar A 1 , …, A n universal to'plamlar U 1 ,…,U n mos ravishda belgilanadi A 1 ´…´A n va to‘plamning loyqa kichik to‘plami sifatida aniqlanadi U 1 ´…´U n a'zolik funktsiyasi bilan.

5.6-misol. Agar a

U 1 \u003d U 2 \u003d 3 + 5 + 7

A 1 =0,5/3+1/5+0,6/7

A 2 \u003d 1/3 + 0,6/5, keyin

A 1 ´A 2 =0,5/3,3+1/5,3+0,6/7,6+0,5/3,5+0,6/5,5+0,6/7,5

Noaniq munosabatlar.

loyqa munosabat R: X®Y Dekart mahsulotining loyqa to'plamidir X´Y. R ikki oʻzgaruvchining aʼzolik funksiyasi yordamida quyidagi tarzda tavsiflanadi:

(5.25)

X´Y to'plamidagi noaniq munosabat juftliklar to'plamidir

(5.26)

qayerda - loyqa munosabatning a'zolik funksiyasi R, bu loyqa to'plam a'zolik funksiyasi bilan bir xil ma'noga ega.

Umuman n- ariy munosabat Dekart mahsulotining noaniq kichik to'plamidir X 1 ´X 2 ´…´X n, va

(5.27)

Noaniq munosabatlarga misollar:

« X taxminan teng Y»,

« X ancha katta Y»,

« LEKIN ancha afzalroq DA».

5.7-misol. Keling, shunday da'vo qilaylik X=(Yuriy, Sergey), Y=(Maksim, Mixail).

U holda X va Y to‘plamlar elementlari orasidagi “o‘xshashlik”ning ikkilik loyqa munosabati quyidagicha yozilishi mumkin.

o'xshashlik=0,8/(Yuriy, Maksim)+0,6/(Yuriy, Mixail)+0,2/(Sergey, Maksim)+0,9/(Sergey, Mixail).

Bundan tashqari, bu munosabat sifatida ifodalanishi mumkin munosabatlar matritsalari.

(5.28)

Qayerda (i, j) - th element for funktsiya qiymatiga teng i- qiymati x va j-chi qiymat y.

Agar a R- munosabat X®Y(yoki, bir xil bo'lgan, munosabatlar X´Y), a S- munosabat Y®Z, keyin kompozitsiya R va S loyqa munosabatdir X®Z, belgilangan R°S va formula bilan aniqlanadi

bu erda ° - kompozitsiyaning belgisi, belgilar Ú va Ù mos ravishda belgilang maks va min, V y- diapazonning yuqori chegarasi da.

Mana (5.29). munosabatlar tarkibi.

(5.29) ifoda maxmin mahsulotini belgilaydi R va S.

Shunday qilib, haqiqiy raqamlar uchun a va b:

(5.30)

(5.31)

Agar a X,Y,Z chekli to'plamlar, keyin munosabat matritsasi R°S munosabat matritsalarining maksimal ko‘paytmasi R va S. Matritsalarning maksimal ko‘paytmasida qo‘shish va ko‘paytirish amali o‘rniga amallar qo‘llaniladi. Ú va Ù mos ravishda.

Maxmin mahsulot namunasi

(5.32)

Bu erda qatorlar soni ustunlar soniga teng bo'lishi kerak. Qator ustunga ko'paytiriladi va maksimal qiymat juftlikning minimal qiymatlaridan olinadi.

3) dan boshqa funktsiya grafigidagi har qanday boshqa nuqta c ix 0,5, masalan, tashuvchining taxminiy chegarasi (x 0,01 ) yoki yadro (x 0,99 ) - b parametrining qiymati natijalar bo'yicha hisoblanadi.

3. Loyqa to'plamlar ustida amallar

Loyqa to'plamlarda operatsiyalarning ikki guruhi mavjud:

1) to'plam nazariyasi operatsiyalar , bular klassik toʻplamlar nazariyasi amallarini loyqa toʻplamlar holiga umumlashtirish;

2) to'plamning loyqaligini hisobga oluvchi amallar

oddiy to'plamlar uchun mantiqiy bo'lmagan xususiyatlar.

Umumiy holda, loyqa to'plamlarda to'plam nazariy amallari shunday aniqlanadiki, aniq to'plamlarga qo'llanilganda, ular odatdagi klassik to'plam nazariy operatsiyalari bilan mos keladi.

Birinchi guruh operatsiyalaridan qo'shish amallarini ko'rib chiqing,

kesishmalar, birlashmalar va kartezyen mahsulotlar , ikkinchi guruh operatsiyalaridan - operatsiya eksponentsiya.

3.1. Qo'shish

A aʼzolik funksiyasi m A boʻlgan X toʻplamdagi noaniq toʻplam boʻlsin. A toʻldiruvchisi aʼzolik funksiyali noaniq A toʻplam boʻlsin.

		(x )= 1− m A (x ),x X

To'ldiruvchi operator odatda mantiqiy NOT modifikatorini ifodalash uchun ishlatiladi.

Loyqa qo'shish operatsiyasini bajarish misoli rasmda ko'rsatilgan. 3.1, shundan ma'lum bo'ladiki, to'plamning o'ziga ham, uning to'ldiruvchisiga ham tegishli bo'lgan ta'rif sohasining elementlari bor, bu elementlar esa ushbu to'plamlarning birortasiga to'liq tegishli emas, a'zolik darajasi 1 ga teng. Boshqalarida. so'zlar bilan aytganda, loyqa mantiq klassik mantiqdan yaxshi ma'lum bo'lgan izchillik printsipi va istisno qilingan o'rta qonuni ishlamaydi, bu aniq tushuncha va uni inkor qilish o'rtasidagi chegaralarning noaniqligi bilan bog'liq.

Loyqa to'plamlar nazariyasining asosiy tushunchalari

Guruch. 3.1. Loyqa qo'shish amalini bajarishga misol

3.2. Chorraha va ittifoq

Loyqa to'plamlarning kesishishi va birlashuvi operatsiyalarini aniqlashning eng keng tarqalgan yondashuvlaridan birini ko'rib chiqing, ba'zan minimaks yondashuv deb ataladi.

A va B mos ravishda m A va m B a’zolik funksiyalariga ega X to‘plamdagi noaniq to‘plamlar bo‘lsin. U holda bu to'plamlarning A ∩ B kesishmasi va A B birlashmasi mos ravishda a'zolik funktsiyalariga ega X da noaniq to'plamlardir:

minimaks yondashuvidan foydalanish shaklda ko'rsatilgan. 3.2.

Guruch. 3.2. Minimaks yondashuvidan foydalangan holda loyqa to'plamlarni kesish va birlashtirish amallarini bajarish misollari

Kesishish amali odatda AND mantiqiy bog‘lovchisini, birlashma amali esa OR bog‘lovchisini ifodalash uchun ishlatiladi.

Ko'rinib turibdiki, agar oddiy aniq to'plamlar A va B operandlari sifatida qabul qilinsa, bu tarzda aniqlangan kesishish va birlashma amallari klassik to'plam nazariy o'xshashlariga qisqartiriladi. Bundan tashqari, ushbu operatsiyalar quyidagi xususiyatlarga ega:

Loyqa to'plamlar nazariyasining asosiy tushunchalari

	kommutativlik:
	A ∩ B= B∩ A, A B= B A;
	assotsiativlik:
	(A∩ B) ∩ C= A∩ (B∩ C) ,
	(A B) C= A(B C) ;
	chegara shartlari:
	A∩=,	A=A
	A ∩ X= A,	AX=X;
	qobiliyatsizlik:
	A ∩ A= A A= A;
	tarqatish qobiliyati:
	A ∩ (B C) = (A ∩ B) (A ∩ C),

A (B ∩ C) = (A B) ∩ (A C).

Loyqa kesishish va birlashma operatsiyalarini aniqlashda ko'rib chiqilgan yondashuv yagona mumkin emas. Ko'pincha boshqa yondashuv qo'llaniladi, unga ko'ra:

m A ∩ B (x )= m A (x )m B (x ),x X ,
m A B (x )= m A (x )+ m B (x )− m A (x )m B (x ),x X .

Ushbu yondashuv ba'zan ehtimollik deb ataladi, chunki tegishli iboralar o'z shaklida tasodifiy hodisalarni kesish va birlashtirish ehtimolini aniqlash uchun ifodalar bilan mos keladi. Ehtimoliy yondashuvdan foydalangan holda kesishish va birlashma operatsiyalarini bajarish misollari rasmda ko'rsatilgan. 3.3.

Guruch. 3.3. Ehtimoliy yondashuv yordamida noaniq to'plamlarni kesish va birlashtirish operatsiyalarini bajarish misollari

Ehtimoliy yondashuv yordamida aniqlangan kesishish va birlashma operatsiyalari uchun kommutativlik va assotsiativlik xususiyatlari, shuningdek chegara shartlari o'z kuchini saqlab qoladi.

Loyqa to'plamlar nazariyasining asosiy tushunchalari

loviya. Idempotentlik va distributivlik xossalari mavjud emas.

mavjud, ammo ularning kamroq qattiq analoglari amal qiladi:

A ∩ A A, A A A;

A ∩ (B C) (A ∩ B) (A ∩ C),

A (B ∩ C) (A B) ∩ (A C).

Loyqa kesishish va birlashma operatsiyalarini aniqlashga kiritilgan yondashuvlar foydalanishga asoslangan umumlashtirilgan yondashuvning maxsus holatlari sifatida ko'rib chiqilishi mumkin. uchburchak normalari va konormlari.

Ikki o'zgaruvchining funksiyasi T (x ,y ) sohasi bo'yicha × (ya'ni, birlik kvadratida), segment bo'yicha qiymatlarni olib, quyidagi shartlarni qondiradigan (x va y ning barcha mumkin bo'lgan qiymatlari uchun) berilsin. ):

1) kommutativlik: T(x, y) = T(y, x);

2) monotonlik: x1 ≤ x2 , y1 ≤ y2 T(x1 , y1 ) ≤ T(x2 , y2 );

3) assotsiativlik: T(T(x, y), z) = T(x, T(y, z));

4) chegara holati: T(x, 1) = T(1, x) = x.

Xuddi shunday, S ( x , y ) funksiyasi bir sohada, segmentdagi qiymatlarni va quyidagi shartlarni qondiradigan barcha mumkin bo'lgan x va y qiymatlari uchun berilgan bo'lsin:

1) kommutativlik: S(x, y) = S(y, x);

2) monotonlik : x1 ≤ x2 , y1 ≤ y2 S(x1 , y1 ) ≤ S(x2 , y2 );

3) assotsiativlik: S(S(x, y), z) = S(x, S(y, z));

4) chegara holati: S(x, 0) = S(0, x) = x.

Keyin T (x ,y ) funksiya chaqiriladi uchburchak normasi yoki

T-norma, S(x, y) esa uchburchak konorm yoki S-normadir.

T-normalari va S-normalariga misollar:

T M (x ,y ) = min(x ,y );	S M (x ,y ) = max(x ,y );
T P (x ,y ) =xy ;	S P (x, y) \u003d x + y -xy;
T L (x, y) \u003d maksimal (x + y -1, 0);	S L (x, y) = min (x + y, 1).

T va S-normalardan foydalanib, loyqa to'plamlarning kesishishi va birlashuvi operatsiyalarining quyidagi umumlashtirilgan ta'rifini kiritishimiz mumkin:

m A ∩ B (x )= T (m A (x ), m B (x )), x X ,
m A B (x )= S (m A (x), m B (x )), x X.

Bu erda T - qandaydir T-norma, S - qandaydir S-norma.

Mantiqiy operatsiyalar

Inklyuziya. Mayli LEKIN va DA- universal to'plamdagi loyqa to'plamlar E. Ular shunday deyishadi LEKIN tarkibida mavjud DA, agar

Belgilash: LEKIN⊂ DA.

Bu atama ba'zan ishlatiladi hukmronlik, bular. qachon bo'lsa LEKIN⊂ DA, shunday deyishadi DA hukmronlik qiladi LEKIN.

Tenglik. Agar A va B teng bo'lsa

Belgilash: A = B.

Qo'shish. Mayli M = , LEKIN va DA da aniqlangan loyqa to'plamlardir E. A va DA agar bir-birini to'ldiradi

Belgilash:

Bu aniq (qo'shimcha uchun belgilangan M= , lekin u har qanday buyurtma uchun aniqlanishi mumkinligi aniq M).

chorraha. LEKIN⋂ DA bir vaqtning o'zida mavjud bo'lgan eng katta loyqa kichik to'plamdir LEKIN va DA:

Uyushma.A∪DA har ikkalasini ham o'z ichiga olgan eng kichik loyqa kichik to'plamdir LEKIN, shunday DA, a'zolik funktsiyasi bilan:

Farq. a'zolik funktsiyasi bilan:

Disjunct summasi

LEKIN ⊕ DA = (A-B) ∪ (B-A) = (A ⋂ ̅ B) ∪ ( ̅A ⋂ B )

a'zolik funktsiyasi bilan:

Misollar. Mayli

Bu yerda:

1) A ⊂ DA, ya'ni A tarkibida mavjud B yoki B hukmronlik qiladi LEKIN; FROM beqiyos bilan ham A, bilan ham emas DA, bular. juftliklar ( A, C) va ( A, C) dominant bo‘lmagan loyqa to‘plamlar juftlaridir.

2) A≠ B ≠ C

3) ̅A = 0,6/x 1 + 0,8/x 2 + 1/x 3 + 0/x 4 ; ̅B = 0,3/x 1 + 0,1/x 2 + 0,9/x 3 +0/x 4 .

4) LEKIN⋂ B = 0,4/x 1 + 0,2/x 2 + 0/x 3 + 1 /X 4 .

5) A∪ DA= 0,7/ x 1+ 0,9/x 2 + 0,1/x 3 + 1/x 4 .

6) A - B= LEKIN⋂̅B = 0,3/x 1 + 0,l/ x 2 + 0/x 3 + 0/x 4 ;

DA- A= ̅A⋂ DA= 0,6/x 1 + 0,8/x 2 + 0,l/ x 3 + 0/x 4 .

7) LEKIN⊕ B = 0,6/x 1 + 0,8/x 2 + 0,1/x 3 + 0/x 4 .

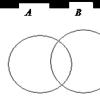
Loyqa to'plamlarda mantiqiy amallarning vizual tasviri. Loyqa to'plamlar uchun siz vizual tasvirni yaratishingiz mumkin. Y o'qida qiymatlari chizilgan to'rtburchaklar koordinatalar tizimini ko'rib chiqing. m A (x), elementlar abscissa o'qida tasodifiy tartibda joylashtirilgan E(biz allaqachon loyqa to'plamlar misollarida bunday tasvirdan foydalanganmiz). Agar a E tabiatan tartibga solingan bo'lsa, x o'qi bo'yicha elementlarni joylashtirishda bu tartibni saqlab qolish maqsadga muvofiqdir. Bunday tasvir loyqa to'plamlarda oddiy mantiqiy amallarni ingl. (1.3-rasmga qarang).

Guruch. 1.3. Mantiqiy operatsiyalarning grafik talqini: α - loyqa to'plam LEKIN; b- loyqa to'plam ̅A, in - LEKIN⋂LEKIN; G- A∪ LEKIN

Shaklda. 1.3a soyali qism loyqa to'plamga mos keladi LEKIN va, aniqrog'i, diapazonni tasvirlaydi LEKIN va tarkibidagi barcha loyqa to'plamlar LEKIN. Shaklda. 1.3 b, c, g beriladi A, A ⋂ ̅ A, A U LEKIN.

Operatsion xususiyatlari ∪ va ⋂

Mayli A, B, C ular loyqa to'plamlar bo'lsa, quyidagi xususiyatlar o'rinli bo'ladi:

Aniq to'plamlardan farqli o'laroq, umuman loyqa to'plamlar uchun

holat:

A⋂̅A ≠∅, A∪ ̅A ≠ E

(bu, xususan, yuqorida loyqa to'plamlarning vizual tasviri misolida tasvirlangan).

Izoh . Loyqa to‘plamlar bo‘yicha yuqoridagi amallar max va min amallardan foydalanishga asoslangan. Loyqa to‘plamlar nazariyasida “va”, “yoki”, “yo‘q” mos bog‘lovchilarining turli semantik soyalarini hisobga olish imkonini beruvchi kesishish, birlashma va to‘ldiruvchining umumlashtirilgan, parametrlangan operatorlarini qurish masalalari ishlab chiqilgan.

Chorraha va birlashma operatorlariga yondashuvlardan biri ularni belgilashdir uchburchak normalari va konormlari sinfi.

uchburchak normasi(t-norma) ikki oʻrinli real funksiya deyiladi T: x → , quyidagi shartlarga javob beradi:

Uchburchak normalariga misollar

min( m A, m B)

ish m A· m B

maksimal (0, m A+ m B- 1 ).

uchburchak konorm(t- muvofiqlik) ikki oʻrinli real funksiya deyiladi S: x → xususiyatlari bilan:

Misollart- konormalar

maksimal( m A, m B)

m A+ m B- m A· m B

min(1, m A+ m B).

Loyqa to'plamlarda algebraik amallar

Algebraik mahsulot A va DA belgilangan A· DA va quyidagicha aniqlanadi:

Algebraik yig'indi bu to'plamlardan belgilangan A+B va quyidagicha aniqlanadi:

(-, +) operatsiyalari uchun quyidagi xususiyatlar bajariladi:

Amalga oshirilmagan:

Izoh. Amallarni ( U, ⋂, + , ) birgalikda ishlatganda quyidagi xususiyatlar bajariladi:

Algebraik mahsulotning ishlashiga asoslanib, operatsiya aniqlanadi eksponentsiya a loyqa to'plam LEKIN, qayerda α ijobiy raqamdir. loyqa to'plam A a a’zolik funksiyasi m a A = m a A () bilan aniqlanadi. x). Eksponentsiyaning alohida holati quyidagilardir:

1) CON( LEKIN) = A 2- operatsiya diqqat (muhrlar);

2) DIL( LEKIN) = A 0,5- operatsiya cho'zish,

lingvistik noaniqliklar bilan ishlashda foydalaniladi (1.4-rasm).

Guruch. 1.4. Konsentratsiyalash (siqilish) va cho'zish operatsiyalari tushunchasi uchun rasm

Raqamga ko'paytirish. Agar a α shunday ijobiy raqam, keyin loyqa to'plamaAa'zolik funktsiyasi mavjud:

m aA (x) = amA(x).

Loyqa to'plamlarning qavariq birikmasi. Mayli A 1 , A 2 ,..., LEKINn- universal to'plamning noaniq to'plamlari E, a ō 1 , ō 2 , …, ōn yig'indisi 1 ga teng manfiy bo'lmagan sonlar.

konveks birikmasi A 1 , LEKIN 2 , ..., LEKINn loyqa to'plam deb ataladi LEKIN a'zolik funktsiyasi bilan:

Kartezian(bevosita) loyqa to'plamlar mahsuloti. Mayli A 1 , LEKIN 2 , ..., LEKINn- universal to'plamlarning noaniq kichik to'plamlari E 1, E 2, ..., En mos ravishda. Dekart yoki to'g'ridan-to'g'ri mahsulot LEKIN = A 1 x A 2 x... x LEKINn to‘plamning loyqa kichik to‘plamidir E = E 1 x E 2 x... x En a'zolik funktsiyasi bilan:

Loyqalikni oshirish operatori aniq to'plamlarni loyqa to'plamlarga aylantirish va loyqa to'plamning loyqaligini oshirish uchun ishlatiladi.

Mayli LEKIN- loyqa to'plam, E- universal to'plam va hamma uchun Xϵ E loyqa to'plamlar aniqlanadi K(x). Hammasining umumiyligi K(x) loyqalikni oshirish operatorining yadrosi deb ataladi F. F operatorining loyqa to'plamdagi harakati natijasi. LEKIN shaklning loyqa to'plamidir

qayerda m A (x) K (x) sonning noaniq to‘plamdagi ko‘paytmasidir.

Misol . Mayli

E =(1,2,3,4); A \u003d 0,8 / 1 + 0,6 / 2 + 0/3 + 0/4; Kimga(1)= 1/1 + 0,4/2;

Kimga(2) = 1/2 + 0,4/1 + 0,4/3; Kimga(3) = 1/3 + 0,5/4; Kimga(4)= 1/4.

Keyin

a-darajani tozalash(yoki a darajasi). Loyqa to'plamning a-darajali to'plami LEKIN universal to'plam E chaqirdi aniq pastki to'plam A a universal to'plam E, shaklida aniqlanadi

Va a ={ x/μ A(x) ≥ α },

qayerda α ≤ 1.

Misol. Mayli A = 0,2/x 1 + 0/x 2 + 0,5/x 3 + 1/x 4, keyin A 0,3 = { x 3 , x 4 } , A 0,7 = {x 4} .

Juda aniq xususiyat: agar a 1≥ 2, keyin Va a1≤ Va a2.

Inklyuziya. A va B universal E to'plamda loyqa to'plamlar bo'lsin. Agar "x OE m A (x) > m B (x) bo'lsa, A B tarkibida mavjud deymiz. Belgisi: A M B.

Tenglik. Agar "xOE m A (x) = m B (x) bo'lsa, A va B tengdir. Belgisi: A = B.

Qo'shish. M =, A va B E da aniqlangan loyqa to'plamlar bo'lsin. A va B agar bir-birini to'ldiradi
"xOE m A (x) = 1 – m B (x). Belgisi: B = yoki A =. Shubhasiz, . (To'ldiruvchi M = uchun aniqlanadi, lekin aniqki, har qanday tartiblangan M uchun aniqlanishi mumkin) .

chorraha. A Ç B - bir vaqtning o'zida A va Bda joylashgan eng katta loyqa kichik to'plam;

m A Ç B(x) = min(m A ( x), m B ( x)}.

Union.A È B a'zolik funktsiyasiga ega bo'lgan A va B ni o'z ichiga olgan eng kichik loyqa kichik to'plamdir

m A È B(x) = maksimal ((m A () x), m B ( x)}.

Farq. LEKIN \ B= A Z a’zolik funksiyasi bilan:

m A \ B ( x) = min ( m A ( x), 1 – m B ( x)}.

Masalan.

Keling: A = 0,4/ x 1 È 0,2/ x 2 È 0/ x 3 È 1/ x 4;

1. A Ì B, ya'ni. A B tarkibida mavjud, C A yoki B bilan taqqoslanmaydi.

2. A ¹ B ¹ C .

3. = 0,6/ x 1 È 0,8/ x 2 È 1/ x 3 È 0/ x 4;
= 0,3/ x 1 È 0,1/ x 2 È 0,9/ x 3 È 0/ x 4.

Loyqa to'plamlar uchun siz vizual tasvirni yaratishingiz mumkin. Y o'qida m A qiymatlari chizilgan to'rtburchaklar koordinatalar tizimini ko'rib chiqing ( x), E ning elementlari x o'qida ixtiyoriy tartibda joylashgan (biz allaqachon loyqa to'plamlar misollarida bunday tasvirdan foydalanganmiz). Agar E tabiatan tartiblangan bo'lsa, x o'qi bo'yicha elementlarni joylashtirishda bu tartibni saqlab qolish maqsadga muvofiqdir. Bunday tasvir loyqa to'plamlardagi oddiy amallarni ingl.

Guruch. 1. rasm. 2

Guruch. 3. rasm. to'rtta.

Shaklda. 1, qorong'u qism loyqa A to'plamiga to'g'ri keladi va aniqrog'i, A diapazoni va A tarkibidagi barcha noaniq to'plamlarni tasvirlaydi. 2-rasmda. 2 – 4 mos ravishda A Ç, AÈ berilgan.

È va Ç operatsiyalarining xossalari.

A, B, C loyqa to'plamlar bo'lsin, u holda quyidagi munosabatlar bajariladi:

a) - kommutativlik;

b) - assotsiativlik;

c) – quvvatsizlik;

G) - distributivlik;

e) AÈÆ = A, qayerda Æ bo'sh to'plamdir, ya'ni. m Æ (x) = 0"xÎE;

AÇE = A, bu erda E - universal to'plam;

e) – De Morgan teoremalari.

Aniq to'plamlardan farqli o'laroq, noaniq to'plamlar uchun umumiy holatda AÇ Æ, AÈ ¹ E, ular, xususan, yuqorida loyqa to'plamlarning vizual tasviri misolida tasvirlangan.

Loyqa to'plamlarda algebraik amallar

A va B ning algebraik mahsuloti A × B bilan belgilanadi va quyidagicha aniqlanadi:

"xOE m A × B ( x) = m A ( x)m B ( x).

Ushbu to'plamlarning algebraik yig'indisi A + B bilan belgilanadi va quyidagicha aniqlanadi:

"xOE m A+V ( x) = m A ( x) + m B ( x)-m A ( x)m B ( x).

Operatsiyalar uchun (×, +) quyidagi xususiyatlar bajariladi:

· – kommutativlik;

· - assotsiativlik;

· A×Æ = Æ, A+Æ = A, A×E = A, A+E = E;

- De Morgan qonunlari.

Amalga oshirilmagan:

· – quvvatsizlik;

· - distributivlik;

va shuningdek, A× = Æ, A+ = E.

De Morganning birinchi qonunini isbotlaylik. m A (x) ni a, m B (x) ni b bilan belgilang. Keyin har bir x element uchun tenglikning chap tomonida bizda: 1 - ab, o'ngda esa algebraik qo'shish formulasiga ko'ra: (1 - a) + (1 - b) - (1 - a) (1 - b) = 1 - ab.

Keling, birinchi taqsimot xususiyatiga ega emasligini isbotlaylik, ya'ni. A × (B + C) ¹ (A × B) + (A × C). Chap tomon uchun bizda: a(b+c – bc) = ab + ac - abc; o'ng uchun: ab + ac - (ab) (ac) = ab + ac + a 2 bc. Demak, distributivlik a¹a 2 uchun amal qilmaydi.

Izoh.(È, Ç,+,×) amallar birgalikda ishlatilsa, quyidagi xossalar saqlanadi:

A×(B È C) = (A×B) È (A × C);

A × (B Ç C) \u003d (A × B) Ç (A × C);

A+(B È C) = (A+B) È (A+C);

A+ (B Ç C) = (A+B) Ç (A+C).

Loyqa to'plamlarning dekart mahsuloti. A 1 , A 2 , ..., A n mos ravishda E 1 , E 2 , ..., E n universal toʻplamlarning loyqa kichik toʻplamlari boʻlsin. Dekart mahsuloti A = A 1 'A 2 ' ...'A n E to'plamining loyqa kichik to'plamidir. = E 1 'E 2 ' ... ´E n a'zolik funktsiyasi bilan:

m A ( x 1 ,x 1 , ...,x n) = min( m A1 ( x 1), m A2 ( x 2) , ... , m Ai ( x n)).

Umumlashtirish printsipi

Loyqa to'plamlar nazariyasining asosiy g'oyalaridan biri bo'lgan umumlashtirish printsipi evristik xususiyatga ega bo'lib, loyqa to'plamlar doirasini xaritalash uchun kengaytirish uchun ishlatiladi. X to‘plamda qiymati Y to‘plamda aniqlangan noaniq f funksiya borligini aytamiz, agar u har bir xOX elementiga m f (x,y) a’zolik darajasiga ega yOY elementni belgilasa. Loyqa funktsiya f loyqa xaritalashni aniqlaydi : X Y.

Umumlashtirish printsipi shundan iboratki, berilgan aniq f uchun: X®Y yoki loyqa f : X da aniqlangan har qanday noaniq A to'plami uchun X Y xaritalash, Y da noaniq f(A) to'plam aniqlanadi, bu A ning tasviri.

f: X®Y berilgan aniq xaritalash va A = (m A (x)/x) X da noaniq to‘plam bo‘lsin. U holda f xaritalash ostidagi A tasviri Y dagi noaniq f(A) to‘plam bo‘lsin. a'zolik funktsiyasi bilan:

m f(A) (y) = ; YOY,

bu yerda f –1 (y)=(x | f(x) = y).

Loyqa xaritalashda f : X Y, har qanday xOX va yOY uchun ikki oʻrinli aʼzolik funksiyasi m f (x, y) aniqlanganda, X da aniqlangan noaniq A toʻplamning tasviri f( loyqa toʻplam boʻladi. A) ustida Y a'zolik funksiyasi bilan m f (A) (y) = ( min(m A (x), m f (x, y) ).

NAZORAT SAVOL VA VAZIFALAR

1. Keling: A = 0,4/ x 1 È 0,2/ x 2 È 0/ x 3 È 1/ x 4;

B = 0,7/ x 1 È 0,9/ x 2 È 0,1/ x 3 È1/ x 4;
C = 0,1/ x 1 È 1/ x 2 È 0,2/ x 3 È 0,9/ x 4.

Konstruksiya to‘plamlari: a) AÇB;

kabina; B \ A.

2. Universal E = (Zaporojets, Jiguli, Mercedes, Ferrari) to'plam uchun to'g'ridan-to'g'ri usul yordamida loyqa to'plamlarni tuzing: a) "yuqori tezlikli";

b) "o'rtacha";

c) "sokin".

3. E = (1, 2, 3, ..., 100) va “yosh” tushunchasiga mos kelsin. Loyqa to'plamlarni qurishning to'g'ridan-to'g'ri usuli

a) "keksalar";

b) "uylanish vaqti keldi";

c) "harbiy majburiyat"

va mos keladigan a'zolik funktsiyalari uchun taxminiy formulani tuzing.

4. 2-masala shartlarida E elementlarini juftlashgan taqqoslash asosida bilvosita usulda noaniq to'plamlarni a) - c) tuzing.

2-BOB. BINAR MUNOSABATLAR

VA FUNKSIYANI TANLASH

Dars raqami 4. Loyqa to'plamlar bilan operatsiyalar

Loyqa to'plamlar bilan bajariladigan amallarning ta'rifi ko'p jihatdan oddiy (aniq) to'plamlar bilan operatsiyalarga o'xshaydi.

Ekvivalentlik. Ikki noaniq to'plam LEKIN va DA ekvivalentdir (bu
) sifatida belgilanadi, agar va faqat bizda mavjud bo'lsa .

Guruch. 2.4. Loyqa to'plamlar bilan operatsiyalar

Inklyuziya. loyqa to'plam LEKIN loyqa to'plamda joylashgan DA() agar va faqat agar

Uyushma, yoki ajratish(dizyunksiya), ikkita loyqa to'plamlar A va B mantiqiy operatsiyaga mos keladi " YOKI" va A va B to'plamlarini o'z ichiga olgan eng kichik loyqa to'plam sifatida aniqlanadi. Bu to'plam uchun a'zolik funksiyasi olish amali yordamida topiladi. maksimal(2.4-rasm, b)

chorraha, yoki birikma(bog'lanish), mantiqiy operatsiyaga mos keladi " Va" va bir vaqtning o'zida ikkala to'plamning kichik to'plami bo'lgan eng katta loyqa to'plam sifatida aniqlanadi.

To‘plamning a’zolik funksiyasi topish amali yordamida ifodalanadi eng kam(2.4-rasm, c)

Qo'shish(to‘ldiruvchi) loyqa to‘plam LEKIN, (yoki ¯| A) bilan belgilanadi, mantiqiy inkorga mos keladi " EMAS"va formula bilan aniqlanadi (2.4-rasm, d)

Ko'rinib turibdiki, a'zolik funktsiyalari faqat 2 ta qiymatni qabul qiladigan klassik "aniq" to'plamlarga nisbatan: 0 yoki 1, formulalar mantiqiy "OR", "VA", "ma'lum operatsiyalarni aniqlaydi. EMAS".

Keling, noaniq to'plamlar bo'yicha yana ikkita juda keng tarqalgan amallarning ta'riflarini beraylik - algebraik mahsulot va loyqa to'plamlarning algebraik yig'indisi.

Algebraik mahsulot AB loyqa to'plamlar LEKIN va DA quyidagicha aniqlanadi:

Algebraik yig'indi:

Yuqoridagilardan tashqari, lingvistik o'zgaruvchilar bilan ishlashda foydali bo'lgan boshqa operatsiyalar ham mavjud.

Operatsiya diqqat(kontsentratsiya) CON(A) loyqa to'plamning algebraik mahsuloti sifatida aniqlanadi LEKIN o'zingizga: bular.

Ushbu operatsiyani to'plamga qo'llash natijasida LEKIN elementlarning a'zolik darajasi kamayadi X bu to'plam va agar bo'lsa, bu pasayish nisbatan kichik, a'zolik darajasi kichik bo'lgan elementlar uchun esa nisbatan katta. Tabiiy tilda bu amalni A lisoniy oʻzgaruvchining u yoki bu qiymatiga nisbatan qoʻllash “juda” (masalan, “juda baland”, “juda eski” va boshqalar) kuchaytiruvchi atamasining qoʻllanilishiga mos keladi.

Operatsiya bukilishlar(kengayish) DIL(A) sifatida aniqlanadi

DIL(A)= A 0,5, qaerda

Ushbu operatsiyaning harakati konsentratsiya operatsiyasiga qarama-qarshi bo'lib, quyidagi (asosiy) atamani zaiflashtirish funktsiyasini bajaradigan noaniq atama "yetarli" ga to'g'ri keladi. LEKIN: "juda baland", "anchalik eski" va boshqalar.

Lingvistik o'zgaruvchining qiymatlarini o'zgartirishga imkon beradigan va shu bilan ularning sonini ko'paytirishga imkon beradigan ma'noga o'xshash boshqa operatsiyalarni kiritish mumkin. Shunday qilib, "ko'proq" atamasi quyidagicha ta'riflanishi mumkin:

"juda-juda" qo'shma atamasi:

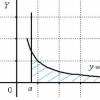
Quyidagi tasviriy misolda ushbu operatsiyalarni qo'llashni ko'rib chiqing. O'zgaruvchiga ruxsat bering X"insonning yoshini" tavsiflaydi, X- interval. Keyin "yosh" va "qari" atamalari bilan tavsiflangan loyqa kichik to'plamlarni a'zolik funktsiyasi yordamida ifodalash mumkin (2.5-rasm).

Guruch. 2.5. "Insonning yoshi" lingvistik o'zgaruvchisining grafik tasviri

Keyin, ifodaga muvofiq, biz topamiz (2.5-rasm)

Xuddi shunday, (2.10) va (2.14) dan foydalanib, biz (2.5-rasm) olamiz.

Misol uchun, agar ma'lum bir shaxs 55 yoshda bo'lsa (ya'ni. X= 55), keyin ushbu a'zolik funktsiyalariga muvofiq bizda:

Hozirgacha biz haqiqiy sonlar o'qi bo'yicha qiymatlarni qabul qiluvchi bitta o'zgaruvchi haqida gapiramiz deb taxmin qilingan.