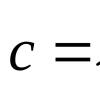Oscillatore armonico.

Un sistema descritto dall'equazione , dove , lo chiameremo oscillatore armonico. La soluzione di questa equazione, come è noto, ha la forma:

.

Pertanto, un oscillatore armonico è un sistema che esegue oscillazioni armoniche attorno a una posizione di equilibrio.

Per un oscillatore armonico valgono tutti i risultati ottenuti in precedenza per un'oscillazione armonica.

Consideriamo e discutiamo due ulteriori questioni.

Lo troveremo impulso oscillatore armonico. Differenziamo l'espressione per t e, moltiplicando il risultato per la massa dell'oscillatore, otteniamo:

Ad ogni posizione caratterizzata da una deviazione “x”, l'oscillatore ha un certo valore “p”. Per trovare "p" in funzione di "x", è necessario escludere "t" dalle equazioni scritte per "p" e "x". Rappresentiamo queste equazioni nella forma:

(8.9)

Elevando al quadrato queste espressioni e sommandole, otteniamo:

. (8.10)

Disegniamo un grafico che mostra la dipendenza dell'impulso “p” dell'oscillatore armonico dalla deviazione “x” (Fig. 8.6). Piano coordinato(“p”, “x”) viene solitamente chiamato piano di fase, e il grafico corrispondente è traiettoria di fase. La traiettoria di fase di un oscillatore armonico è un'ellisse con semiassi “A” e “A m w 0”. Ogni punto della traiettoria di fase rappresenta lo stato dell'oscillatore per un certo momento nel tempo (cioè la sua deviazione e la sua quantità di moto). Nel tempo, il punto che rappresenta lo stato si muove lungo la traiettoria della fase, compiendo un circuito completo durante il periodo di oscillazione. Inoltre, questo movimento avviene in senso orario [vale a dire, se ad un certo punto nel tempo t¢ x=A, p=0, allora a momento successivo il tempo “x” diminuirà e “p” assumerà un modulo crescente valori negativi, cioè. lo spostamento del punto pittorico (cioè del punto che rappresenta lo stato) avverrà in senso orario].

Troviamo ora l'area dell'ellisse. O

.

Qui , dove n 0 è la frequenza naturale dell'oscillatore, che è un valore costante per un dato oscillatore.

Quindi, . Dove

Così, energia totale l'oscillatore armonico è proporzionale all'area dell'ellisse e il coefficiente di proporzionalità è la frequenza naturale dell'oscillatore.

8.6. Piccole oscillazioni del sistema in prossimità della posizione di equilibrio.

Consideriamo un sistema meccanico arbitrario, la cui posizione può essere specificata utilizzando una singola quantità “x”. Il valore “x” che determina la posizione del sistema può essere un angolo misurato da un certo piano o una distanza misurata lungo una data curva.

L'energia potenziale di un tale sistema sarà funzione di una variabile “x”: E p = E p (x).

Scegliamo l'origine in modo che nella posizione di equilibrio x=0. Allora la funzione E p (x) avrà un minimo in x=0.

(a causa della piccolezza di “x” trascuriamo i restanti termini)

Perché E p (x) a x=0 ha un minimo, quindi , e . Denotiamo E p(x) = b e , Poi .

Questa espressione è identica all'espressione per l'energia potenziale di un sistema in cui agisce una forza quasi elastica (la costante “b” può essere posta uguale a 0).

La forza che agisce sul sistema può essere determinata dalla formula: . Ottenuto tenendo conto che il lavoro viene svolto a causa della perdita di energia potenziale.

Quindi, l'energia potenziale del sistema per piccole deviazioni dalla posizione di equilibrio risulta essere funzione quadratica spostamento e la forza che agisce sul sistema ha la forma di una forza quasi elastica. Di conseguenza, con piccole deviazioni dalla posizione di equilibrio, qualsiasi sistema meccanico eseguirà vibrazioni prossime all'armonica.

8.7. Pendolo matematico.

DEFINIZIONE: pendolo matematico chiameremo sistema idealizzato costituito da un filo senza peso e inestensibile su cui è sospesa una massa concentrata in un punto.

La deviazione del pendolo dalla posizione di equilibrio sarà caratterizzata dall'angolo j (Fig. 8.7). Quando il pendolo si discosta dalla posizione di equilibrio si verifica un momento rotazionale , ha una direzione tale che tende a riportare il pendolo nella posizione di equilibrio, quindi bisogna assegnare segni diversi al momento M e allo spostamento angolare j.

Consideriamo le oscillazioni di un peso m su una molla con coefficiente di rigidezza k, che giace su una tavola piana orizzontale, assumendo che non vi sia attrito del peso sulla superficie della tavola. Se il peso viene rimosso dalla sua posizione di equilibrio, oscillerà rispetto a questa posizione. Descriveremo queste oscillazioni con una funzione dipendente dal tempo, considerando che determina la deviazione del peso dalla sua posizione di equilibrio al tempo t.

Nella direzione orizzontale, sul peso agisce solo una forza: la forza elastica della molla, determinata dalla famosa legge di Hooke

La deformazione della molla è funzione del tempo, per cui è anche variabile.

Dalla seconda legge di Newton abbiamo

poiché l'accelerazione è la derivata seconda dello spostamento: .

L'equazione (9) può essere riscritta nella forma

Dove. Questa equazione è chiamata equazione dell’oscillatore armonico.

Commento. Nella letteratura matematica, quando si scrive un'equazione differenziale, l'argomento (t) solitamente non è indicato vicino a tutte le funzioni che dipendono da esso. Questa dipendenza è presupposta per impostazione predefinita. Quando si utilizza il pacchetto matematico Maple in (10), è necessario indicare una dipendenza esplicita della funzione.

A differenza di esempio precedente moto di un corpo sotto l'azione di una forza costante, nel nostro caso la forza cambia nel tempo e l'equazione (10) non può più essere risolta utilizzando la consueta procedura di integrazione. Proviamo a indovinare la soluzione di questa equazione, sapendo che descrive un processo oscillatorio. Come una delle possibili soluzioni dell'equazione (10), puoi scegliere la seguente funzione:

Funzione di differenziazione (11), abbiamo

Sostituendo l'espressione (12) nell'equazione (10), ci assicuriamo che sia soddisfatta in modo identico per qualsiasi valore di t.

Tuttavia, la funzione (11) non lo è l'unica soluzione equazioni dell'oscillatore armonico. Come ulteriore soluzione potete ad esempio scegliere una funzione che può essere controllata facilmente in modo simile. Inoltre, si può verificare che qualsiasi combinazione lineare di queste due soluzioni con nomi casuali

con coefficienti costanti A e B è anche una soluzione dell'equazione dell'oscillatore armonico.

Si può dimostrare che la soluzione (13), che dipende da due costanti, è una soluzione generale dell'equazione dell'oscillatore armonico (10). Ciò significa che la formula (13) esaurisce tutto possibili soluzioni questa equazione. In altre parole, l'equazione dell'oscillatore armonico non ha altre soluzioni parziali, eccetto quelle ottenute dalla formula (13) fissando costanti arbitrarie A e B.

Si noti che in fisica è molto spesso necessario cercare alcune soluzioni particolari delle singole ODE o dei loro sistemi. Consideriamo questo problema in modo più dettagliato.

Si possono eccitare oscillazioni nel sistema di un peso su una molla che stiamo considerando diversi modi. Poniamo le seguenti condizioni iniziali

Ciò significa che dentro momento iniziale tempo, il peso è stato retratto dalla posizione di equilibrio di una quantità a ed è stato rilasciato liberamente (cioè inizia il suo movimento con velocità iniziale zero). Si possono immaginare molti altri metodi di eccitazione, ad esempio impartire ad un peso in posizione di equilibrio una certa velocità iniziale mediante un "clic", ecc. [generalmente,].

Consideriamo le condizioni iniziali (14) come alcune condizioni supplementari isolare dalla soluzione generale (13) qualche soluzione particolare corrispondente al nostro metodo di eccitare le oscillazioni del peso.

Assumendo t=0 nell'espressione (13), abbiamo, il che implica che B=a. Pertanto, abbiamo trovato una delle costanti precedentemente arbitrarie nella soluzione (13). Successivamente, differenziando nella formula (13), abbiamo

Assumendo t=0 in questa espressione e tenendo conto della seconda condizione iniziale dalla (14), otteniamo, ne consegue che A=0 e, quindi, la soluzione particolare iniziale ha la forma

Descrive la modalità oscillatoria del sistema meccanico in esame, che è determinata dalle condizioni di eccitazione iniziale (14).

È noto dal corso di fisica scolastica che nella formula (16) a è l'ampiezza delle oscillazioni (specifica la deviazione massima del peso dalla sua posizione di equilibrio), è la frequenza ciclica ed è la fase delle oscillazioni (la fase iniziale è uguale a zero).

L'equazione dell'oscillatore armonico (10) è un esempio di ODE lineare. Ciò significa che la funzione incognita e tutte le sue derivate compaiono in ogni termine dell'equazione al primo grado. Le equazioni differenziali lineari sono estremamente importanti caratteristica distintiva: Soddisfano il principio di sovrapposizione. Ciò significa che qualsiasi combinazione lineare di due soluzioni qualsiasi di un'ODE lineare è anche la sua soluzione.

Nell'esempio che stiamo considerando dell'equazione dell'oscillatore armonico, una combinazione lineare arbitraria di due soluzioni particolari non è solo una nuova soluzione, ma una soluzione generale a questa equazione (esaurisce tutte le sue possibili soluzioni).

In generale, questo non è il caso. Ad esempio, se avessimo a che fare con linear equazione differenziale terzo ordine, (cioè se l'equazione includesse una derivata terza), allora anche una combinazione lineare di due qualsiasi delle sue soluzioni parziali sarebbe una soluzione a questa equazione, ma non la rappresenterebbe decisione comune.

In un corso sulle equazioni differenziali, si dimostra un teorema secondo cui la soluzione generale di una EDO di ordine N (lineare o non lineare) dipende da N costanti arbitrarie. Quando equazione non lineare queste costanti arbitrarie possono entrare nella soluzione generale (a differenza della (13)) in modo non lineare.

Il principio di sovrapposizione gioca un ruolo esclusivo nella teoria ODE. ruolo importante, poiché con il suo aiuto è possibile costruire una soluzione generale di un'equazione differenziale sotto forma di sovrapposizione delle sue soluzioni particolari. Ad esempio, per il caso delle ODE lineari a coefficienti costanti e dei loro sistemi (l’equazione dell’oscillatore armonico si riferisce specificamente a questo tipo di equazioni), si è sviluppata la teoria delle equazioni differenziali metodo generale soluzioni. La sua essenza è la seguente. Nella forma si cerca una soluzione particolare. Come risultato della sua sostituzione nell'equazione originale, tutti i fattori dipendenti dal tempo vengono cancellati e si arriva ad una certa equazione caratteristica, che per l'N-esimo ordine ODE è equazione algebrica Ennesimo grado. Risolvendolo, troviamo così tutte le possibili soluzioni parziali, una combinazione lineare arbitraria delle quali dà la soluzione generale dell'ODE originale. Non ci soffermeremo ulteriormente su questo tema, rimandando il lettore ai corrispondenti libri di testo sulla teoria delle equazioni differenziali, nei quali si possono trovare ulteriori dettagli, in particolare la considerazione del caso in cui l'equazione caratteristica contiene radici multiple.

Se si considera un'ODE lineare a coefficienti variabili (i suoi coefficienti dipendono dal tempo), allora è valido anche il principio di sovrapposizione, ma si costruisce in qualche modo una soluzione generale esplicita a questa equazione metodo standard, non è più possibile. Torneremo più avanti su questo argomento, discutendo il fenomeno della risonanza parametrica e l'equazione di Mathieu associata al suo studio.

Consideriamo un semplice sistema fisico: un punto materiale capace di oscillare su una superficie orizzontale senza attrito sotto l'influenza della forza di Hooke (vedi Fig. 2).

Se lo spostamento del carico è piccolo (molto inferiore alla lunghezza della molla non deformata) e la rigidezza della molla è uguale a k, allora l'unica forza che agisce sul carico è la forza di Hooke. Poi l'equazione

il movimento del carico (seconda legge di Newton) ha la forma

Spostando i termini a sinistra dell'uguaglianza e dividendo per la massa del punto materiale (trascuriamo la massa della molla rispetto a m), otteniamo l'equazione del moto

(*) ,

,

,

periodo di oscillazione.

Quindi, assumendo la funzione

ed avendolo differenziato rispetto al tempo, siamo convinti, in primo luogo, che la velocità di spostamento del carico è pari a

e in secondo luogo, dopo ripetute differenziazioni,

,

cioè X(t) è realmente una soluzione dell'equazione del carico su una molla.

Tale sistema, in generale, qualsiasi sistema, meccanico, elettrico o altro, che abbia un'equazione del moto (*), è chiamato oscillatore armonico. Una funzione di tipo X(t) è chiamata legge del moto di un oscillatore armonico, la quantità
sono chiamati ampiezza,ciclico O frequenza naturale,fase iniziale. La frequenza naturale è determinata dai parametri dell'oscillatore, l'ampiezza e la fase iniziale sono specificate dalle condizioni iniziali.

La legge del moto X(t) rappresenta le oscillazioni libere. Tali oscillazioni vengono eseguite da pendoli non smorzati (matematici o fisici), corrente e tensione in un circuito oscillatorio ideale e alcuni altri sistemi.

Le oscillazioni armoniche possono sommarsi sia in una che in direzioni diverse. Anche il risultato dell'addizione è un'oscillazione armonica, ad esempio:

.

Questo è il principio della sovrapposizione (sovrapposizione) delle vibrazioni.

I matematici hanno sviluppato una teoria delle serie di questo tipo, chiamate serie di Fourier. Esistono anche una serie di generalizzazioni come gli integrali di Fourier (le frequenze possono variare continuamente) e persino gli integrali di Laplace che funzionano con frequenze complesse.

§15. Oscillatore smorzato. Vibrazioni forzate.

Vero sistemi meccanici avere sempre almeno un po' di attrito. Il caso più semplice è l'attrito liquido o viscoso. Questo è l'attrito, la cui entità è proporzionale alla velocità di movimento del sistema (ed è diretta, naturalmente, contro la direzione del movimento). Se il movimento avviene lungo l'asse X, allora l'equazione del moto può essere scritta (ad esempio, per un peso su una molla) nella forma

,

Dove – coefficiente di attrito viscoso.

Questa equazione del moto può essere trasformata nella forma

.

Qui
– coefficiente di attenuazione, – è ancora la frequenza naturale dell’oscillatore (che non può più essere definita armonica; è un oscillatore smorzato per attrito viscoso).

I matematici possono risolvere tali equazioni differenziali. È stato dimostrato che la soluzione è la funzione

L'ultima formula utilizza la seguente notazione: – ampiezza iniziale, frequenza delle oscillazioni debolmente smorzate
,
. Inoltre, vengono spesso utilizzati altri parametri che caratterizzano l'attenuazione: decremento dell'attenuazione logaritmica
, tempo di rilassamento del sistema
, fattore di qualità del sistema
, dove il numeratore è l'energia immagazzinata dal sistema e il denominatore è la perdita di energia nel periodo T.

In caso di forte attenuazione
la soluzione ha forma aperiodica.

Ci sono spesso casi in cui, oltre alle forze di attrito, sull'oscillatore agisce una forza esterna. Quindi l'equazione del moto viene ridotta alla forma

,

l'espressione a destra è spesso chiamata forza ridotta, l'espressione stessa
chiamata forza coercitiva. Per una forza motrice arbitraria, non è possibile trovare una soluzione all'equazione. Solitamente si considera una forza motrice armonica del tipo
. Allora la soluzione rappresenta una parte smorzata del tipo (**), che tende a zero per tempi ampi, e oscillazioni costanti (forzate)

Ampiezza oscillazioni forzate

,

e la fase delle oscillazioni forzate

.

Si noti che quando la frequenza naturale si avvicina alla frequenza della forza motrice, l'ampiezza delle oscillazioni forzate aumenta. Questo fenomeno è noto come risonanza. Se lo smorzamento è elevato, l’aumento della risonanza non è elevato. Questa risonanza è chiamata “opaca”. A basse attenuazioni, l'ampiezza della risonanza “forte” può aumentare in modo abbastanza significativo. Se il sistema è ideale e non vi è attrito, l'ampiezza delle oscillazioni forzate aumenta illimitatamente.

Si noti anche che alla frequenza della forza motrice

Si ottiene il valore massimo dell'ampiezza della forza motrice, pari a

.

Oscillazioni di un oscillatore armonico Oscillatore armonicoè un oggetto fisico la cui evoluzione nel tempo è descritta dall'equazione differenziale

Dove Q– coordinata generalizzata dell’oscillatore armonico, T- tempo, ? – frequenza caratteristica di un oscillatore armonico. Due punti sopra la variabile indicano la derivata seconda rispetto al tempo. Grandezza Q eseguire oscillazioni armoniche.
Il problema dell’oscillatore armonico gioca un ruolo centrale sia nella fisica classica che in quella quantistica.
Un gran numero di i sistemi fisici si comportano come oscillatori armonici con piccole deviazioni dall'equilibrio. Questi includono pendoli matematici e fisici, vibrazioni di atomi in molecole e solidi, circuiti oscillatori elettrici e molti altri.
Piccole oscillazioni di un pendolo sono armoniche

Energia, funzione Lagrange e Hamilton
Energia cinetica oscillatore armonico è dato dall'espressione

L'energia potenziale di un oscillatore armonico è data dall'espressione

Di conseguenza, considerando il valore Q coordinata generalizzata, si scrive la funzione di Lagrange dell'oscillatore armonico

.

Impulso generalizzato

Funzione di Hamilton

.

Vibrazioni forzate
Sotto l'influenza di una forza periodica esterna con una frequenza che non coincide necessariamente con la frequenza naturale dell'oscillatore armonico, l'oscillatore esegue oscillazioni armoniche, la cui ampiezza è determinata dall'entità della forza esterna e dal rapporto tra la forza esterna frequenza e la frequenza naturale dell'oscillatore.
Oscillazioni forzate di un oscillatore armonico con frequenza? 0 sotto l'influenza di una forza con una frequenza descritta dall'equazione?

Dove F 0 – ampiezza della forza esterna.
Una soluzione particolare di questa equazione che descrive le oscillazioni forzate ha la forma

.

Un oscillatore armonico sotto l'influenza di una forza esterna esegue oscillazioni armoniche con un'ampiezza . Quando l'ampiezza delle oscillazioni forzate tende all'infinito. Questo fenomeno è chiamato risonanza.
Oscillatore armonico con smorzamento
Se si prendono in considerazione le forze di attrito o di resistenza di altro tipo, che portano alla dissipazione dell'energia dell'oscillatore e alla sua conversione in calore, l'equazione dell'oscillatore armonico cambia. In particolare, un caso molto comune è quando le forze di resistenza sono proporzionali alla velocità di variazione della quantità Q. Quindi assume la forma l'equazione dell'oscillatore armonico

Tali oscillazioni decadono nel tempo secondo la legge

Oscillazioni forzate di un oscillatore armonico con smorzamento
Sotto l'azione di una forza esterna periodica, anche con attenuazione, si stabiliscono oscillazioni armoniche per l'oscillatore con un'ampiezza che dipende dalla forza applicata, dal rapporto di frequenza e anche dall'entità dell'attenuazione.
L'ampiezza delle oscillazioni forzate, tenendo conto dello smorzamento, è determinata dalla formula

.

Questo è un valore finito a tutte le frequenze della forza esterna.
Un pendolo matematico con una piccola deviazione iniziale dalla verticale esegue oscillazioni armoniche con una frequenza

Circuito oscillatorio con un oscillatore armonico, con una frequenza

Dove L è l'induttanza, C è la capacità.
Vedi Oscillatore Quantistico per maggiori dettagli.
Spettro di autovalori e autofunzioni
Funzioni d'onda dei primi sei stati con numeri quantici da N= da 0 a 5. La coordinata generalizzata è tracciata sull'asse delle ordinate. L'Hamiltoniano dell'oscillatore armonico si ottiene sostituendo la quantità di moto nella funzione Hamiltoniana P SU

.

Lo spettro dell'oscillatore armonico è con equazione stazionaria Schrödinger ed è dato dalla formula

.

Qui N– numero quantico, va da zero a infinito. I livelli energetici dell'oscillatore armonico sono equidistanti. Caratteristica oscillatore armonico è che anche nello stato fondamentale l'oscillatore armonico ha energia diversa da zero

Questo bassa energia chiamato energia di oscillazioni nulle.
Autofunzioni dell'oscillatore armonico corrispondenti al numero quantico N sono dati da formule

,

Dove un Hn(x)– Polinomi di Hermite.
Quando pari N le autofunzioni dell'oscillatore armonico sono pari, mentre per Nepranu sono dispari. L'Hamiltoniana dell'oscillatore armonico commuta con l'operatore di sostituzione X SU - X(operatore di parità), e quindi ha autofunzioni comuni con questo operatore.
Operatori di nascita e distruzione
Se definiamo l'operatore di nascita

E l'operatore della distruzione

,

.

Gli operatori di creazione e distruzione soddisfano la relazione di commutazione:

Le autofunzioni dell'oscillatore armonico hanno quindi la forma

Oppure, usando la notazione vettoriale ket e bra:

L'azione totale dell'operatore nascita sull'operatore armonico è nello stato | n> porta ad una transizione allo stato | n+1>:

Azione dell'operatore di distruzione sullo Stato | n> porta ad una transizione allo stato | n-1>:

Operatore

È chiamato operatore del numero di particelle perché per esso vale la relazione.

Regole di selezione
Quando un fotone viene emesso o assorbito, le transizioni consentite per un oscillatore armonico sono quelle in cui il numero quantico n cambia di uno. Tenendo conto della natura equidistante dei livelli, questa regola di selezione porta al fatto che, nonostante numero infinito livelli, nello spettro di assorbimento ottico o radiazione di un oscillatore armonico c'è solo una linea con frequenza?.
Negli spettri vibrazionali reali delle molecole, sono possibili deviazioni da questa regola a causa dell'anarmonicità del potenziale di interazione interatomico reale, delle transizioni del quadrupolo, ecc.

Il modello più semplice movimento oscillatorio gli atomi in una molecola biatomica possono fungere da sistema di due masse T/ e w?, collegati da una molla elastica. La vibrazione di due atomi rispetto al centro di massa può essere sostituita dalla vibrazione di un equivalente

massa rispetto al punto zero iniziale R= 0, dove

R- distanza tra le masse, Rif- posizione del punto di equilibrio.

Nella considerazione classica si assume che la molla sia ideale - la forza elastica F è direttamente proporzionale alla deformazione - lo scostamento dall'equilibrio x = R-R e, secondo la legge di Hooke:

Dove A- costante elastica. Pertanto, la forza è diretta verso il ritorno alla posizione di equilibrio.

Utilizzando insieme le leggi di Hooke e di Newton (F-ta), si può scrivere:

(indicando ). È noto che la soluzione di tale equazione è

svolgere funzioni armoniche

Dove xo- ampiezza e

Utilizzando la massa ridotta /l noi abbiamo:

Una misura dell'energia potenziale di un sistema V serve lavoro

Nella meccanica quantistica, l'analisi del moto oscillatorio per un semplice modello di oscillatore armonico è piuttosto complessa. Si basa sulla risoluzione dell'equazione di Schrödinger

(sì/- funzione d'onda vibrazionale, E - energia totale particelle) e va oltre lo scopo della nostra presentazione.

Per un oscillatore quantistico, secondo la formula è possibile solo una serie discreta di valori di energia E e frequenze E=hv. Inoltre, il valore minimo dell'energia dell'oscillatore non è zero. Questa quantità è chiamata energia di punto zero, corrisponde al livello energetico più basso dell'oscillatore ed è pari a , la sua esistenza può essere spiegata in base alla relazione di indeterminazione di Heisenberg.

Pertanto, in conformità con meccanica quantistica l'energia dell'oscillatore armonico è quantizzata:

Dove v- numero quantico vibrazionale, che può assumere il valore y=0, 1, 2, 3,....

Quando un oscillatore interagisce con i quanti radiazioni elettromagnetiche Dovrebbero essere presi in considerazione tre fattori: 1) popolazione di livelli (la probabilità che una molecola si trovi a un dato livello energetico); 2) la regola della frequenza (Bohr), secondo la quale l'energia di un quanto deve corrispondere alla differenza nell'energia di due livelli qualsiasi;

3) regola di selezione per transizioni quantistiche: probabilità di transizione, ovvero l'intensità delle linee nello spettro di assorbimento è determinata dalla quantità momento di dipolo di transizione (vedi introduzione teorica). Nel caso dell'oscillatore armonico più semplice, la regola di selezione si ottiene considerando le funzioni d'onda. Afferma che le transizioni possono avvenire solo tra livelli adiacenti (“un passo”): il numero quantico vibrazionale cambia di uno Avv= 1. Poiché le distanze tra livelli adiacenti sono le stesse, lo spettro di assorbimento di un oscillatore armonico dovrebbe contenere solo una linea con frequenza

Poiché, secondo la distribuzione di Boltzmann a temperatura ambiente e altro ancora basse temperature Se è popolato il livello vibrazionale più basso, la transizione dal livello più basso (d=0) è più intensa e la frequenza di questa linea coincide con la frequenza delle transizioni più deboli dai livelli più alti al livello vicino più alto.

Grafici delle funzioni d'onda dell'oscillatore armonico per significati diversi le energie sono mostrate nella Figura 2.3. Rappresentano soluzioni dell'equazione di Schrödinger per un oscillatore armonico

Dove N, - fattore normalizzante, H0- Polinomi di Hermite, x = R-R e- deviazione dalla posizione di equilibrio.

Momento dipolare di transizione per transizioni vibrazionali, R0(O M") uguale a:

Dove ju- momento dipolare della molecola; esitazione

corpo funzioni d'onda rispettivamente stati iniziali e finali. Dalla formula è chiaro che la transizione è consentita,

se nel punto di equilibrio - il momento dipolare della molecola

cambia vicino alla posizione del punto di equilibrio, (curva ju=f(R) non passa attraverso il massimo a questo punto). Anche l'integrale (il secondo fattore nella formula) non deve essere uguale a zero. Si può dimostrare che questa condizione è soddisfatta se la transizione avviene tra livelli adiacenti, da qui la regola di selezione aggiuntiva Ai = 1.

Nel caso delle molecole biatomiche, gli spettri vibrazionali possono essere osservati solo per le molecole eteronucleari; per le molecole omonucleari non esiste momento dipolare e non cambia durante le vibrazioni. Gli spettri vibrazionali della CO2 mostrano vibrazioni (stiramento e flessione antisimmetrici), in cui il momento dipolare cambia, ma non compaiono vibrazioni simmetriche, in cui rimane invariato.